[딥러닝] Attention is all you need 논문 번역
업데이트:
Attention is all you need 논문 번역
0. Abstract
대부분의 시퀀스 변환 모델들은 복잡한 순환신경망(RNN)이나 합성곱신경망(CNN)을 기반으로 하는 경우가 많았고, 이러한 신경망들은 인코더(encoder)와 디코더(decoder)를 포함한다. 또한 성능이 가장 뛰어난 모델들은 어텐션 메커니즘을 통해 인코더와 디코더를 연결한다. 우리는 이 논문에서 트랜스포머(Transformer)라는 아주 단순한 신경망 구조를 제안한다. 이 트랜스포머라는 구조는 RNN이나 CNN은 제거하고 단순히 어텐션 메커니즘을 기반으로 하는 아주 간단한 구조이다. 우리는 번역 업무를 수행하는 두 종류의 인공지능으로 실험을 했는데, 트랜스포머 기반의 모델이 품질이 더 우수했으며 병렬처리 하기 좋고, 학습하는 시간도 적게들었다. 우리 모델은 WMT 2014 영어-독일어 번역 업무에서 28.4 BLEU를 기록했는데, 이는 기존 기록보다 2 BLEU 이상 좋은 성능을 보여주면서 기존 베스트 기록을 갈아치웠다. 그리고 WMT 2014 영어-프랑스 번역 업무에서는 단일 모델 기준, 41.8 BLEU라는 초대 신기록을 달성했는데, 이는 3.5일 동안 8개의 GPU로 학습한 결과이고 흔히 말하는 베스트 모델에 비해 현저히 적은 리소스로 학습한 것을 의미한다. 트랜스포머 구조는 대규모 학습 데이터냐 제한된 학습 데이터냐에 상관없이 영어 구문 분석에서 성공적으로 적용할 수 있음을 보여주었다.
1. Introduction
RNN, LSTM, GRU와 같은 모델들은 언어 모델이나 기계번역과 같은 시퀀스 모델링이나 변환 문제에서 대세로 자리잡았습니다. 그리고 인코더-디코더 아키텍트를 발전시키기 위한 수많은 사람들의 노력이 있었다.
순환 모델들은 일바적으로 인풋이나 아웃풋 시퀀스의 기호 위치를 따라 팩터를 계산한다.
시퀀스의 기호 위치는 계산 과정에서 특정 스텝에 할당딘 후,
은닉 상태 $h_t$를 생성합니다.
이때 은닉 상태 $h_t$는 이전 은닉상태 $h_{t-1}$과 현재 시점 $t$에서의 인풋값의 함수이다.
그러나 이러한 방식으로는 학습과정에서 데이터의 병렬 처리를 어렵게 만들고 시퀀스 길이가 길어질수록 더 큰 문제가 된다.
왜냐하면 메모리 제약조건이 데이터간 배치를 제한하기 때문이다.
최근 연구에서는 팩토라이제이션 트릭과 조건부 계산을 활용해 계산 효율성을 높이고,
조건부 계산의 경우에는 모델 성능도 끌어올렸다.
그러나 순차적으로 계산된다는 근본적인 제약조건은 여전히 남아있는 상태였다.
어텐션은 인풋/아웃풋 시퀀스 내의 거리에 상관없이 의존성을 모델링 가능하게 만들어, 다양한 작업에서 강력한 시퀀스 모델링 통합이나 변환 모델의 필수 요소가 되었다. 그러나 일부 예외케이스를 제외하면 이러한 어텐션 메커니즘은 대부분 RNN과 함께 사용된다.
이 연구에서는 RNN을 배제하고, 대신 어텐션 메커니즘만을 사용해 인풋과 아웃풋 간의 의존성을 모델링하는 Transformer라는 모델 아키텍처를 제안한다. Transformer는 병렬 처리를 대폭 향상 시키며, 8개의 P100 GPU에서 단 12시간의 훈련만으로 번역에서 최고의 성능을 보여준다.
2. Background
순차적 계산을 줄이기 위한 목표는 Extended Neural GPU, ByteNet, ConvS2S와 같은 모델들의 기반을 형성한다. 이러한 모델들은 기본적으로 CNN을 사용하며 모든 인풋/아웃풋 위치에 대해 은닉 표현(hidden representation)을 병렬처리로 계산한다. 그리고 이러한 모델들은 엄청난 양의 연산을 요구한다. 왜냐하면 임의의 두 인풋 또는 아웃풋 위치 간의 신호를 연결하는데 필요한 연산 횟수가 위치간 거리에 따라 증가하기 때문이다. ConvS2S는 선형적으로, ByteNet의 경우 로그 함수 형태로 증가한다. 이는 먼 위치간의 의존성을 학습하는 것을 더 어렵게 만든다. 반면, 트랜스포머에서는 연산 횟수가 상수형태로 일정하다는 장점이 있지만, 이를 위해 어텐션 가장치가 적용된 위치를 평균화하기 때문에 모델이 정보를 구분하고 세밀하게 표현하는 능력이 감소한다는 단점이 있다. 이러한 효과는 3.2절에서 설명한 Multi-Head Attention을 통해 보완한다.
Self-attention은 때로 intra-attention이라고도 불리는데, 이는 하나의 시퀀스 내의 서로 다른 위치들을 연관지어 그 시퀀스의 표현(representation)을 계산하는 어텐션 메커니즘이다. Self-attention은 다양한 역할을 수행하는데, 예를 들어, 독해, 요약, 텍스트 함의 분석 등과 같은 문장 표현 학습을 포함한 다양한 역할을 수행한다.
End-to-end 메모리 네트워크는 시퀀스 정렬된 순환 대신 순환 어텐션 메커니즘을 기반으로 하며, 간단한 언어 질문 답변 및 언어 모델링 관련해서는 좋은 성능을 보이는 것으로 알려져있다. 여기서 시퀀스 정렬(sequence alignment)라는 말은 입력 시퀀스의 각 위치가 시간 순서대로 단계별로 처리되는 것을 의미한다.
우리가 아는 한 트랜스포머는 시퀀스 정렬된 RNN이나 합성곱 없이도 인풋/아웃풋 표현을 계산하기 위해 self-attention만 사용하는 최초의 변환 모델이다. 다음 섹션에서는 트랜스포머를 설명하고, self-attention을 사용하는 이유를 알아보며, 다른 모델에 비해 가지는 장점에 대해 논의해보자.
3. Model Architecture
대부분의 뛰어난 신경망 기반 시퀀스 변환 모델들은 인코더-디코더 구조로 구성되어 있다. 이 구조에서 인코더는 인풋 시퀀스 $x=(x_1, … , x_n)$를 $z=(z_1, …, z_n)$로 매핑한다. 이때 $x$는 (“I”,”love”,”you”)와 같은 기호 표현을 의미하고, $z$는 ((0.2, 0.3, -0.1),(0.5, -0.4, 0.2),(-0.1, 0.8, 0.3))과 같은 연속형 숫자 표현을 의미한다. 그 후에 디코더는 $z$를 기반으로 출력 시퀀스 $(y_1, …, y_m)$을 한번에 하나씩 생성한다. 이때 디코더는 자기회귀(auto-regressive) 방식으로 작동하며, 이전에 생성된 기호들을 다음 기호를 생성할 때 추가적인 입력으로 사용한다.
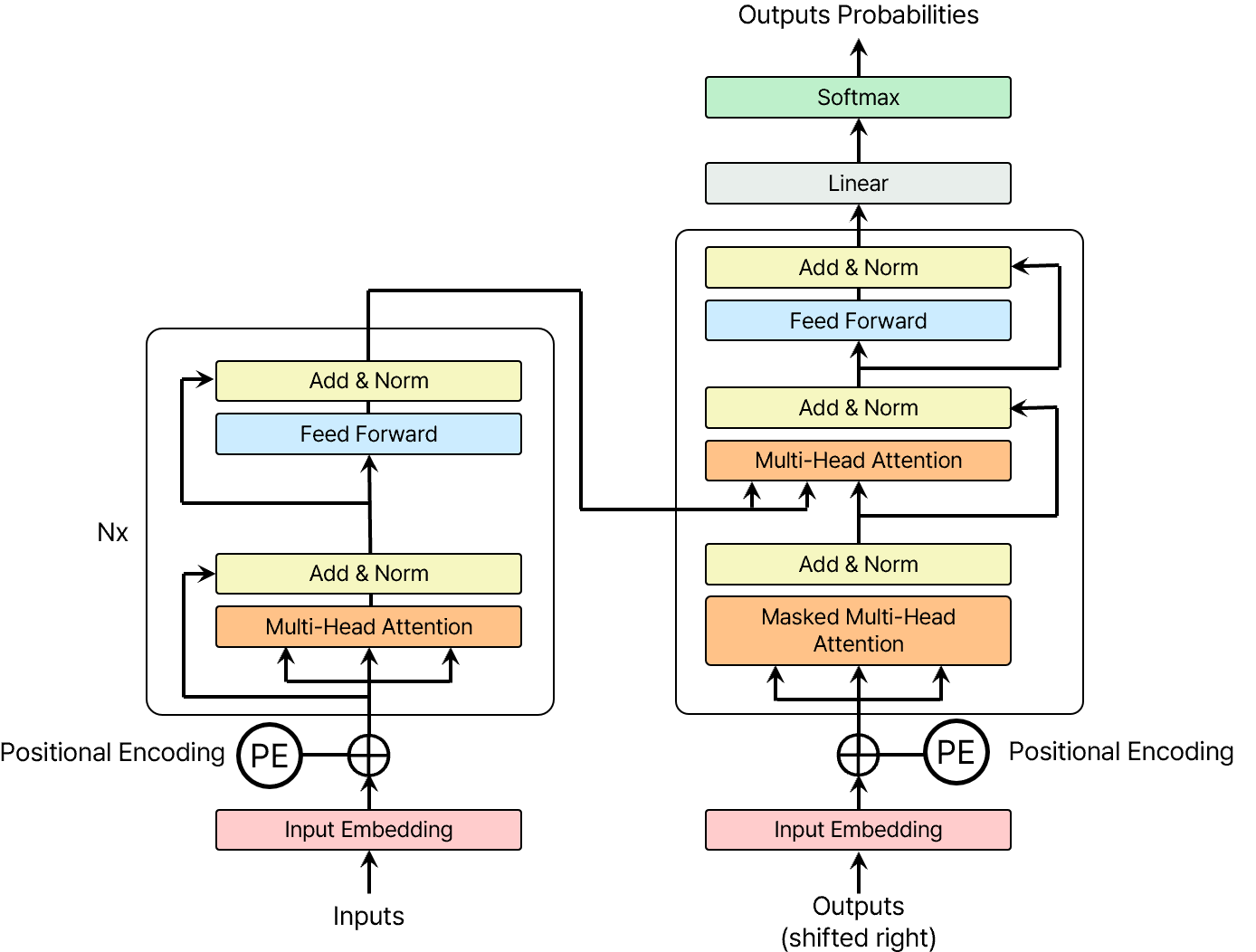
Figure 1. The Transformer - model architecture
트랜스포머는 위 그림과 같은 전체적은 구조를 따른다. 이 트랜스포머는 self-attention을 쌓은 형태와 각각의 단어가 별도로 처리되는(point-wise) 완전 연결(full connected) 레이어를 활용해 인코더와 디코더를 구성한다.
이 구조는 figure1의 왼쪽과 오른쪽 그림에서 각각 볼 수 있다. 왼쪽 그림은 인코더 구조, 오른쪽 그림은 디코더 구조를 보여준다. 인코더와 디코더는 각각 self-attention 메커니즘을 통해 입력 시퀀스 간의 관계를 계산하고, 이어지는 full connected layer를 통해 최종 출력을 생성한다.
3.1. Encoder and Decoder Stacks
Encoder
인코더는 $N=6$개의 동일한 레이어로 구성된 스택 구조이다.
그리고 각 레이어는 두개의 서브 레이어를 포함한다.
첫 번째 서브 레이어는 Multi-head self attention 메커니즘으로,
인풋 시퀀스 내의 위치 간 의존성을 계산한다.
두 번째 서브 레이어는 각각의 단어가 별도로 처리되는(position-wise)
완전 연결(full connected) 피드포워드 네트워크로,
인풋 데이터를 개별적으로 처리하며 비선형 변환을 수행한다.
이렇게 두개의 서브레이어 주변에는 잔차 연결(residual connection) 후에
레이어 normalizaiton을 사용한다.
즉, 각 서브 레이어의 아웃풋은 다음과 같다.
인풋 $x$와 인풋 $x$가 서브레이어를 통과한 아웃풋인 $sublayer(x)$를 더한 다음
normalizaiton을 수행한다. 이를 수식으로 나타내면 다음과 같다.
$LayerNorm(x + sublayer(x))$
이러한 잔차연결을 용이하게 하기 위해서, 모델 내부의 임베딩 레이어를 포함한 모든 서브 레이어에 아웃풋 차원 $d_{model}=512$로 설정한다.
Decoder
디코더는 $N=6$개의 동일한 레이어로 구성된 스택 구조를 가진다. 각각의 레이어에는 두개의 서브 레이어가 존재하는것 까지는 인코더 레이어와 유사하지만 디코더에는 세번째 서브 레이어가 추가되는데, 세번째 서브레이어는 인코더 스택의 아웃풋에 대해 multi-head attention을 수행한다. 인코더와 유사하게, 서브 레이어 주변에 잔차 연결을 하고 normalization을 수행한다. 반면, 디코더 내부에 있는 self-attention 서브 레이어를 수정하여 특정 위치가 현재 이후에 나오는 위치를 참조하지 못하도록 한다. 즉, 미래 정보를 참조하지 못하도록 막는다는 뜻이다. 이러한 마스킹은 출력 임베딩이 오프셋만큼 이동된다는 사실과 결합되어 $i$번째 위치의 예측이 $i$ 이전 위치에서 알려진 아웃풋에만 의존할수있도록 보장한다.
3.2 Attention
어텐션 함수는 쿼리와 키-값 쌍의 집합을 아웃풋으로 매핑하는 방식으로 설명할 수 있다.
이때 쿼리(query), 키(key), 값(value), 아웃풋(output) 모두 벡터로 표현된다.
아웃풋은 값(value)의 가중합으로 계산되며,
각 값에 할당된 가중치는 해당 쿼리와 대응되는 키(key) 사이의 호환성 함수에 의해 계산된다.
예를들어 “I love apples”라는 문장을 번역하는 모델을 처리중이라고 했을때,
디코더가 “사과”라는 단어를 생성하려고 하는 상황이라고 가정하자.
이때 쿼리(query)는 디코더의 현재상태이며,
현재상태는 사과와 관련된 정보를 찾아야하는 상태를 의미이다.
쿼리를 예로 들면 (0.25, 0.35, 0.45)와 같은 벡터 형태를 띈다.
키(key)와 값(value)는 인코더가 입력 문장의 각 단어를 벡터로 변환한 단서다.
- “I” -> key: (0.1, 0.2, 0.3), value: (0.5, 0.6, 0.7)
- “love” -> key: (0.2, 0.3, 0.4), value: (0.6, 0.7, 0.8)
- “apples” -> key: (0.3, 0.4, 0.5), value: (0.7, 0.8, 0.9)
아웃풋은 쿼리와 키 간의 유사도를 계산해 가장 관련성 높은 값들을 가중합한 값이다.
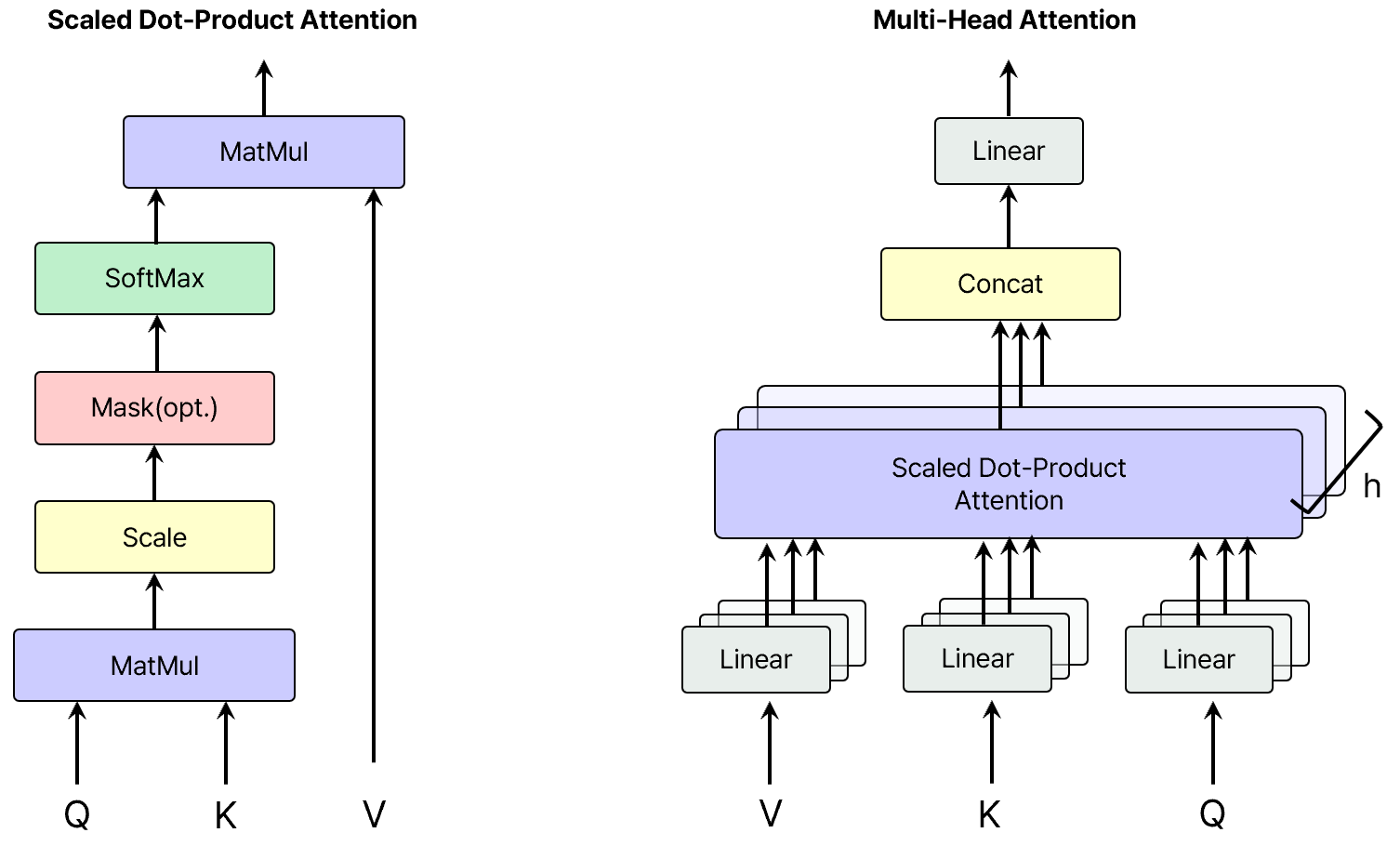
Figure2. 왼쪽) Scaled Dot-Product Attention, 오른쪽) 병렬로 실행되는 레이어로 구성된 멀티 헤드 어텐션
3.2.1 Scaled Dot-Product Attention
우리는 이 특정한 어텐션 방식을 “Scaled Dot-Product Attention”이라고 부르겠다. (figure2 참고) 인풋 데이터는 $d_k$ 차원의 쿼리와 키(key)와 $d_v$ 차원의 값(value)으로 구성되어 있다. 우리는 쿼리와 키 간의 내적을 계산한 뒤, 각 결과를 $\sqrt{d_k}$로 나누고 소프트맥스 함수를 적용해 값(value)에 대한 가중치를 얻는다.
실제로는 동시에 여러 쿼리들에 어텐션 함수를 적용하고, 행렬 Q에 함께 모아서 처리한다. 키와 값들 역시 행렬 k와 v에 함께 모아처리한다. 우리는 아웃풋 해열을 다음과 같이 계산할 수 있다.
$Attention(Q, K, V) = softmax(\frac{QK^{T}}{\sqrt{d_k}})V$
가장 흔하게 사용되는 어텐션 함수는 additive(가산) attention과 dot-product(내적) 어텐션이다. 내적 어텐션은 $1/\sqrt{d_k}$ 스케일링 요소만 추가된 것을 제외하면 우리 알고리즘(Scaled Dot-Product Attention)과 동일하다. 가산 어텐션은 호환성 함수를 계산할 때, 단일 은닉층을 가진 피드포워드 네트워크를 사용한다. 이러한 두 방식은 이론적인 복잡도가 비슷하지만, 내적 어텐션은 매우 최적화된 행렬 곱셈 코드로 구현할 수 있으므로 실제로 훨씬 빠르고 메모리 효율적이다. 즉, 가산 어텐션은 은닉층을 활용해 호환성을 계산하고, 내적 어텐션은 단순히 내적을 사용하는데, 내적 어텐션이 더 빠르고 효율적이라고 할 수 있다.
$d_k$가 작을 때는 두 방법의 성능이 비슷하지만 $d_k$가 클 경우에는 스케일링이 없는 내적 어텐션은 가산 어텐션보다 성능이 떨어진다. $d_k$ 값이 클 경우, 내적 결과값이 매우 커지면서 소프트맥스 함수의 그래디언트가 매우 작은 영역(region)으로 밀려서 그런것이 아닐까 추측한다. 따라서 이러한 일을 예방하고 안정성을 확보하기 위해 내적 값에 $1/\sqrt{d_k}$을 곱하는 스케일링을 적용한다.
3.2.2 Multi-Head Attention
우리는 $d_{model}$ 차원의 키, 값, 쿼리를 사용해 단일 어텐션 함수를 수행하는 대신,
쿼리 키, 값을 각각 서로 다르게 학습된 프로젝션(linear projections)을 사용해
$d_k$, $d_k$, $d_v$ 차원으로 프로젝션(linear projections)하고
이를 h번 반복하는 것이 유리하다는 것을 발견했다.
이렇게 선형 변환된 쿼리, 키, 값에 대해 각각 병렬로 어텐션 함수를 수행하여
$d_v$차원의 아웃풋을 얻는다.
이 아웃풋들을 이어 붙여 서로 연결(concatenate)하고 다시 한번 선형 변환 한 뒤,
figure2에 묘사된 것과 같은 최종 값을 구할 수 있다.
멀티-헤드 어텐션은 모델이 다양한 표현 공간(Representation Subspace)에서 서로 다른 위치의 정보를 동시에 주목할 수 있게 한다. 단일 어텐션 헤드에서는 평균화로 인해 여러 정보가 하나로 합쳐지면서 구체적인 특징들이 희석될 수 있다. 그러나 멀티-헤드 방식은 각 헤드가 독립적으로 특정 특징을 학습할 수 있게 함으로써 모델의 표현력을 강화시킨다. 쉽게 말해서 여러개의 어텐션 헤드를 사용해 다양한 정보에 동시에 집중하는 것이다.
$MultiHead(Q, K, V) = Concat(head_1, …, head_h)W^{O}$
$where head_i = Attentino(QW_{i}^{Q}, KW_{i}^{K}, VW_{i}^{V})$
이때 프로젝션(projection, 선형 변환)에 사용되는 행렬들은 다음과 같은 매게변수 행렬로 정의 된다.
$W_{i}^{Q}\in \mathbb{R}^{d_{model} \times d_k}$
$W_{i}^{K}\in \mathbb{R}^{d_{model} \times d_k}$
$W_{i}^{V}\in \mathbb{R}^{d_{model} \times d_v}$
$W_{i}^{O}\in \mathbb{R}^{hd_{v} \times d_{model}}$
3.2.3 Applications of Attention in our Model
트랜스포머는 다음과 같은 3가지 방법으로 멀티-헤드 어텐션을 사용한다.
-
‘인코더-디코더 어텐션’ 레이어에서는 쿼리가 이전 디코더 레이어에서 생성되고, 메모리 키와 값은 인코더 출력에서 가져온다. 이러한 방법은 디코더의 모든 위치가 입력 시퀀스의 모든 위치에 주목할 수 있도록 한다. 이러한 방식은 [38, 2, 9]와 같은 시퀀스-투-시퀀스 모델에서 사용되는 일반적인 ‘인코더-디코더 어텐션’ 메커니즘을 사용한다. 즉, 인코더 디코더 어텐션은 디코더가 입력 전체 시퀀스 정보에 접근할 수 있게 해주는 메커니즘이다.
-
인코더는 셀프 어텐션(self-attention) 레이어을 포함하고 있다. 셀프 어텐션 레이어에서는 키, 값, 쿼리 모두 동일한 출처(place)로부터 생성되며, 여기서는 인코더의 이전 계층 아웃풋에서 나옵니다. 여기서 동일한 출처라는 말에 대해 알아보자. 일반적인 어텐션 메커니즘에서는 쿼리, 키, 값이 서로 다른 데이터 소스에서 올수 있다. 예를 들어 인코더-디코더 어텐션에서 쿼리는 디코더 아웃풋에서 생성되며 키와 값은 인코더 아웃풋에서 생성된다. 반면 셀프 어텐션에서는 쿼리, 키, 값이 모두 동일한 소스(ex. 이전 레이어 아웃풋, 인풋 데이터)에서 생성된다.
-
유사하게, 디코더의 셀프 어텐션 레이어는 디코더의 각 위치가 해당 위치까지의 모든 위치에 주목(attend)할 수 있도록 한다. auto-regressive 특성을 유지하기 위해 디코더에서 왼쪽 방향으로 정보가 흐르는 것(leftward information flow)을 방지해야한다. 이때, 왼쪽 방향으로 흐르는 것은 현재 위치 이후의 미래 단어가 과거로 정보를 제공하는 것을 의미한다. 이를 구현하기 위해 스케일 조정된 내적 어텐션(scaled dot-product attention)내에서 소프트맥스 인풋 중 불법적인 연결에 해당하는 모든 값을 마스킹 처리해 $-\infty$로 설정한다. Figure2를 참고하자.
3.3 Position-wise Feed Forward Networks
어텐션 서브 레이어 외에도 추가적으로, 인코더와 디코더의 각 레이어는 완전 연결(fully connected) 네트워크를 포함하며, 이는 각 위치에 개별적이고 동일하게 적용된다. 이 네트워크는 두 개의 선형 변환과 그 사이의 ReLU 활성화 함수로 구성된다.
$FFN(x)=max(0, xW_1 + b_1)W_2 + b_2$
선형 변환(linear transformation)은 다른 위치에도 전반적으로 걸쳐서 동일하지만, 레이어마다 서로 다른 파라미터를 사용한다. 이를 다르게 표현하면, 커널 크기가 1인 두개의 합성곱(convolution)으로 설명할 수 있다. 입력과 출력의 차원은 $d_{model}$, 내부 레이어의 차원은 $d_{ff}=2048$이다.
3.4 Embeddings and Softmax
다른 시퀀스 변환 모델과 유사하게, 우리는 학습된 임베딩을 사용하여 인풋 토큰과 아웃풋 토큰을 $d_{model}$ 차원의 벡터로 변환한다. 우리는 또한 디코더의 아웃풋을 다음 토큰의 예측 확률로 변환하기 위해, 학습된 선형 변환(linear transformation)과 소프트맥스 함수를 사용한다. 여기서 학습된 선형 변환이란 우리가 흔히 알고 있는 $wx + b$를 의미한다. 우리 모델에서는, 두개의 임베딩 레이어(인풋, 아웃풋)와 소프트맥스 이전 선형 변환 간 동일한 가중치 행렬을 공유한다. 이는 (30)에서 사용된 방법과 유사하다. 임베딩 레이어에서, 우리는 가중치 행렬에 $\sqrt{d_{model}}$을 곱한다.
Table 1: 다양한 레이어 유형에 대한 최대 경로 길이(Maximum path length), 레이어별 연산 복잡도(Per-layer complexity), 최소 순차 연산 수 (Minimum number of sequential operations)
| Layer Type | Complexity per Layer | Sequential Operations | Maximum Path Length |
|---|---|---|---|
| Self-Attention | $O(n^2 \cdot d)$ | $O(1)$ | $O(1)$ |
| Recurrent | $O(n \cdot d^2)$ | $O(n)$ | $O(n)$ |
| Convolutional | $O(k \cdot n \cdot d^2)$ | $O(1)$ | $O(log_k (n))$ |
| Self-Attention(restricted) | $O(r \cdot n \cdot d)$ | $O(1)$ | $O(n/r)$ |
3.5 Positional Encoding
우리 모델은 순환(recurrence)이나 합성곱(convolution)을 사용하지 않으므로, 시퀀스의 순서 정보를 활용하려면 토큰의 상대적 또는 절대적 위치 정보를 추가해야 한다. 이를 위해 포지셔널 인코딩(positional encoding)을 인풋 인베딩에 추가한다. 이는 인코더와 디코더 스택의 가장 바닥(bottom)에서 적용된다. 포지셔널 인코딩은 임베딩과 동일한 차원($d_{model})$을 가지며, 두 값을 합산 할 수 있도록 설계된다. 포지셔널 인코딩 방식에는 여러가지 선택지가 있는데, 학습 기반 방식과 고정(fixed) 방식이 있다.
포지셔널 인코딩은 시퀀스 내 각 토큰의 위치 정보를 벡터로 표현하여, 모델이 순서를 이해할 수 있게 한다. 이때 위에서 말한 고정 방식이란 주로 수학에서 말하는 사인이나 코사인 함수를 말한다.
- “I love you”
- “I” -> (0.5, 0.6, 0.7, 0.8)
- “love” -> (0.6, 0.7, 0.8, 0.9)
- “you” -> (0.7, 0.8, 0.9, 1.0)
예를 들어, 위와 같이 시퀀스 길이가 3이라고 하고, 임베딩 차원 $d_{model}=4$라고 하면 포지셔널 인코딩은 다음과 같다.
- 짝수 인덱스($2i$) : $sin(\frac{pos}{10000^{2i / d_{model}}})$
- 홀수 인덱스($2i+1$) : $cos(\frac{pos}{10000^{2i / d_{model}}})$
위 식은 짝수 차원은 사인 함수로 계산하고 홀수 차원은 코사인 함수로 계산하라는 뜻이다. 위와 같은 함수를 선택한 이유는, 해당 함수들을 사용했을 때 모델이 상대적인 위치를 쉽게 학습할 수 있을 것이라고 가정했기 때문이다. 왜냐하면 고정된 오프셋 k에 대해 $PE_{pos+k}$는 $PE_{pos}$의 선형함수로 표현될수 있기 때문이다. 이 말은 특정 위치에서 고정된 간격만큼 떨어진 다른 위치의 인코딩 값은 원래 위치의 인코딩 값과 선형적으로 연관되도록 설계된다는 뜻이다. 예를 들어 위 예제에서 I는 love 바로 앞에 있다라는 관계를 모델이 쉽게 이해할 수 있다.
예를 들어, 위 예제에서 “love”에 해당하는 단어는 포지션 1에 해당한다. 참고로 I는 포지션 0, you는 포지션 2에 해당함. 이를 POS=1이라고 하고 POS=1에 대해 포지셔널 인코딩을 진행하면 다음과 같다.
- $i=0$, PE(1, 0) = $sin(\frac{1}{10000^{0/4}}) = sin(1) = 0.0001$
- $i=1$, PE(1, 1) = $cos(\frac{1}{10000^{0/4}}) = cos(1) = 0.0001$
- $i=2$, PE(1, 2) = $sin(\frac{1}{10000^{2/4}}) = sin(1/100) = 0.9999$
- $i=3$, PE(1, 3) = $cos(\frac{1}{10000^{0/4}}) = cos(1/1000) = 0.9999$
위와 같이 정리하면 “love”에 대한 포지셔널 인코딩은 다음과 같다.
$PE(1) = [0.0001, 0.9999, 0.0001, 0.9999]$
그리고나서 기존 인풋 인베딩에 포지셔널 인코딩을 추가하면 다음과 같다.
- “I” -> (0.5, 0.6, 0.7, 0.8) -> (0.5, 1.6, 0.7, 0.8)
- “love” -> (0.6, 0.7, 0.8, 0.9) -> (0.6001, 1.6999, 0.8001, 1.8999)
- “you” -> (0.7, 0.8, 0.9, 1.0) -> (0.7002, 1.7998, 0.9002, 1.9998)
위와 같은 고정 방식 말고도, 우리는 학습된 포지셔널 임베딩을 사용하는 실험도 진행했다. 사인, 코사인 기반 인코딩과 학습된 임베딩과 같은 두 방식이 거의 동일한 결과를 산출한다는 것을 발견했다. (표 3의 E행 참고) 우리는 사인파 기반 버전을 선택했는데, 이는 이 방식이 모델이 학습 중에 만나는 시퀀스 길이보다 더 긴 시퀀스에 대해 외삽(extrapolate)을 가능하게 하기 때문이다. 이때, 외삽은 학습 데이터 범위 밖에 있는 값을 추정하거나 예측하는 것을 의미한다. 예를 들어 학습 데이터에서 길이 10까지의 문장만 학습했다면, 길이 15의 문장을 처리하려는 시도가 외삽이다. 예를 들어, 내가 학습할 때 사용한 데이터는
- “I love deep learning because it is fun.”
와 같이 단어 9개로 구성된 문장이었다면 실제 테스트 상황에서는 다음과 같이 17개 단어로 구성된 문장이 들어올 수 있다.
- “The Transformer model is very powerful and works well for long sequences in natural language processing.”
위와 같은 경우, 학습된 포지셔널 임베딩을 사용할 경우, 학습 데이터에 등장했던 문장 길이에만 최적화되므로 학습 중에는 본적없는 길이 17의 문장에 대해서는 제대로 동작하지 않을수도 있다. 반면 사인파 기반 포지셔널 인코딩을 사용하는 경우, 문장의 길이가 길어지더라도 그대로 적용 가능하다.
4. Why Self-Attention
이번 섹션에서는 시퀀스 $(x_1, … ,x_n)$을 동일한 길이의 다른 시퀀스 $(z_1, … ,z_n)$로 매핑하는 데 일반적으로 사용되는 순환 레이어와 합성곱 레이어를 셀프 어텐션과 다양한 측면으로 비교한다. 이때 $x_i, z_i \in R^d$를 만족하는데 $x_i, z_i$는 스칼라가 아니라 벡터이며, 이들은 시퀀스 변환하는 인코더나 디코더에 있는 은닉 상태(hidden state) 벡터을 의미한다. 셀프 어텐션을 사용하기 위해서는 우리는 세가지 필요조건을 고여한다.
첫번째 필요조건은 레이어 당 총 계산 복잡도이다. 예를 들어 연산에 필요한 곱셈과 덧셈의 수 등을 합산하여 계산한다. 두번째 조건은 병렬화 할 수 있는 계산의 양인데, 이는 필요한 최소 순차 연산의 수로 측정된다. 이때, 병렬화 가능한 정도를 평가하기 위해 순차적으로만 수행해야하는 최소 작업수를 기준으로 삼는다는 점이다. 순차 작업이 적을 수록 병렬 처리가 더 효과적일 수 있다.
세번째 조건은 네트워크 내에서 장거리 의존성 간의 경로 길이(path length)이다. 여기서 장거리 의존성이란 시퀀스 내에서 서로 멀리 떨어진 단어 간의 관계를 의미한다. 이런 경우, 두 점을 연결하는 경로의 길이가 중요하다. 장거리 의존성을 학습하는 것은 많은 시퀀스 변환 작업에서 중요한 과제이다. 예를 들어 수많은 번역이나 음성처리에서 문장의 앞부분과 뒷부분의 관계를 학습한다. 이러한 의존성 학습에 영향을 미치는 주요 요인 중 하나는 네트워크에서 순방향 신호와 역방향 신호가 이동해야하는 경로의 길이이다. 신호가 짧은 경로로 전달될수록, 정보 손실이 줄어들며 학습이 더 쉬워진다. 이처럼 인풋/아웃풋 시퀀스의 모든 위치 조합 간 경로가 짧을수록, 장거리 의존성을 학습하기 더 쉬워진다. 따라서 우리는 서로 다른 레이어 유형으로 구성된 네트워크에서 모든 입력 및 출력 위치 간 최대 경로 길이를 비교한다.
표 1에서 언급한 바와 같이, 셀프 어텐션 레이어는 모든 위치를 상수 개수의 순차적으로 실행되는 연산으로 연결하는 반면, 순환 신경망 레이어는 O(n)개의 순차적인 연산을 요구한다. 즉, 셀프 어텐션은 모든 위치를 한번에 처리하는데, 순환 신경망은 시퀀스를 순차적으로 처리해야하므로 시간이 더 걸린다는 의미이다. 계산 복잡도 측면에서, 셀프 어텐션 레이어는 시퀀스 길이 n이 표현 차원 d보다 작을 때 순환 레이어보다 더 빠르다. (대부분의 경우 문장 길이는 표현 차원보다 짧기 때문에 셀프 어텐션이 더 효율적이다. 예를 들어 “I love you”는 문장에 3개의 단어가 있으므로 문장 길이는 3이 되고, I를 (0.2, 0.3, 0.5, 0.4, 0.1)로 표현한다면 단어를 나타내는 표현 차원은 5가 된다. ) 이는 단어 조각(word-piece)이나 바이트 쌍(byte-pair) 표현과 같은 최신 기계 번역 모델에서 사용하는 문장 표현에 해당하는 경우가 많다. 매우 긴 시퀀스를 처리하는 작업에서 계산 성능을 개선하기 위해, 셀프 어텐션은 입력 시퀀스에서 각각의 출력 위치를 중심으로 하는 크기 r의 이웃만 고려하도록 제한될 수 있다. 이렇게 하면 최대 경로 길이는 O(n/r)로 증가한다. 우리는 이 접근 방법을 향후 연구에서 더 조사할 계획이다.
단일 합성곱 계층은 커널 너비 k가 n보다 작을 때, 인풋과 아웃풋 위치간의 모든 쌍을 연결하지 못한다. 즉, k가 문장 길이보다 작으면 한번의 합성곱으로는 전체 입력과 출력 간의 관계를 연결할 수 없다는 뜻이다. 이 문제를 해결하려면 연속적인 커널(contiguous kernels)를 사용할 경우 O(n/k)개의 합성곱 레이어를 쌓아야하며, dilated convolution을 사용할 경우 $O(log_k(n))$ 레이어가 필요하다. 이는 경로의 길이를 늘려서 더 많은 계층을 쌓아야 한다는 것을 의미한다. 결과적으로 합성곱 레이어은 인풋과 아웃풋 간의 모든 관계를 연결하려면 더 많은 계층을 필요하므로 긴 경로를 다루기 어렵다는 의미이다. 합성곱 레이어는 일반적으로 순환 레이어보다 계산 비용이 k배 더 비싸다. 여기서 k는 커널 크기인데, 이 커널 크기만큼 계산 비용이 증가한다. 분리 가능한 합성곱(separable convolutions)을 사용하면 계산 복잡돌ㄹ 크게 줄일 수 있다. 이 경우, 계산 복잡도는 $O(k\cdot n \cdot d + n\cdot d^2)$로 줄어든다. 이때, n은 시퀀스 길이, d는 표현 차원이다. 분리 가능한 합성곱에서 $k=n$일 경우, 그 계싼 복잡도는 셀프 어텐션 계층과 포인트-와이즈(point-wise) 순전파 레이어의 조합과 동일한데, 이는 우리가 사용하는 방식이다.
셀프 어텐션 모델은 좀 더 해석 가능한 모델을 만들수 있다는 장점이 있다. 즉, 모델이 어떤 방식으로 작동하는지 더 쉽게 이해할 수 있다는 뜻이다. 우리는 모델에서 나온 어텐션 분포를 분석하고, 그 예시를 부록에 포함했다. 여기서 어텐션 분포란, 모델이 인풋 데이터에서 어느 부분에 집중하는지를 나타내는 값을 의미한다. 개별적인 어텐션 헤드(attention head)가 각기 다른 task를 학습하는 것이 분명할 뿐만 아니라, 많은 경우 구문(syntactic)과 의미(semantic) 구조와 관련된 행동을 보이는 것처럼 보인다. 즉, 모델이 문장에서 문법적인 구조와 의미적인 관계를 잘 이해하고 있다는 뜻이다.
5. Training
이번 섹션에서는 우리 모델의 학습 체계에 대해 알아보자.
5.1 Training Data and Batching
우리는 약 450만개의 문장 쌍으로 구성된 표준 WMT 2014 영어-독일어 데이터셋을 활용해 학습을 진행했다. 문장들은 바이트 쌍 인코딩(Byte-Pair Encoding, BPE)을 사용해 인코딩 했으며, 이 방식은 약 37,000개의 토큰으로 이루어진 공유된 소스-타켓 어휘를 가진다. 예를 들어 소스 어휘가 영어이고 “I”라면 타겟 어휘 독일어는 “Ich”가 된다. 영어-프랑스어의 경우, 36M개의 문장으로 구성된 WMT 2014 영어-프랑스어 데이터셋을 사용했고, 32000개의 어휘(vocabulary)로 분할했다. 문장 쌍은 대략적인 시퀀스 길이에 따라 배치로 묶었다. 학습 배치에는 약 25000개의 소스 토큰과 25000개의 타겟 토큰이 포함된 문장 쌍들이 포함되었다.
5.2 Hardware and Schedule
우리는 8개의 엔비디아 P100 GPU가 장착된 한대의 머신에서 모델을 학습시켰다. 본 논문에 설명된 하이퍼 파라미터를 사용한 기본 모델에서는 각 학습 단계마다 약 0.4초가 걸렸다. 우리는 기본 모델을 총 100,000 단계를 12시간 동안 훈련시켰다. 우리는 큰 모델(표 3의 가장 아래에 설명된 모델들)에서는 각 학습 단계마다 1초가 걸렸고, 300,000 단계, 즉, 3.5일 동안 학습 시켰다.
5.3 Optimizer
우리는 Adam 옵티마이저를 사용했으며, $\beta_1 = 0.9, \beta_2=0.98, \epsilon=10^{-9}$로 설정했다. 학습률 같은 경우에는 학습하는 과정에서 다음과 같은 식을 따르게끔 적용해서 다양한 학습율을 적용시켰다.
$lrate = d_{model}^{-0.5}\cdot min(stepnum^{-0.5}, stepnum\cdot warmupsteps^{-1.5})$
이는 첫번째 warmupsteps 학습 단계 동안 학습률을 선형적으로 증가시키고, 그 이후에는 학습률을 학습 단계 수의 제곱근의 역수에 비례하여 감소시키는 방식이다. 그리고 우리는 warmupsteps를 4000으로 설정했다.
5.4 Regularization
우리는 학습할 때 세가지 유형의 정규화 방식을 적용했다.
Table2. 트랜스포머는 이전의 최신 모델들보다 영어-독일어와 영어-프랑스어 newstest2014에서 더 높은 BLEU 점수를 달성했으며, 학습 비용은 더 적게 들어간다.
| Model | EN-DE BLEU | EN-FR BLEU | EN_DE Cost | EN-FR Cost |
|---|---|---|---|---|
| ByteNet | 23.75 | |||
| Deep-Att + PosUnk | 39.2 | $1.0\cdot 10^{20}$ | ||
| GNMT + RL | 24.6 | 39.92 | $2.3\cdot 10^{19}$ | $1.4\cdot 10^{20}$ |
| ConvS2S | 25.16 | 40.46 | $9.6\cdot 10^{18}$ | $1.5\cdot 10^{20}$ |
| MoE | 26.03 | 40.56 | $2.0 \cdot 10^{19}$ | $1.2\cdot 10^{20}$ |
| Dep-Att+ PosUnK Ensemble | 40.4 | $8.0\cdot 10^{20}$ | ||
| GNMT + RL Ensemble | 26.30 | 41.16 | $1.8 \cdot 10^{20}$ | $1.1\cdot 10^{21}$ |
| ConvS2S Ensemble | 26.36 | 41.29 | $7.7 \cdot 10^{19}$ | $1.2\cdot 10^{21}$ |
| Transformer(base model) | 27.3 | 38.1 | $3.3 \cdot 10^{18}$ | $3.3 \cdot 10^{18}$ |
| Transformer(big) | 28.4 | 41.8 | $2.3 \cdot 10^{18}$ | $2.3 \cdot 10^{18}$ |
Residual Dropout. 우리는 각 서브 레이어의 아웃풋에 드롭아웃을 적용한 후, 그것을 서브 레이어의 인풋에 더하고 정규화했다. 또한 인코더와 디코더 스택에서 임베딩과 포지셔널 인코딩의 합에 드롭아웃을 적용했다. 기본 모델에서는 드롭아웃 비율로 $P_{drop}=0.1$로 적용했다.
Label Smoothing. 학습하는 동안 $\epsilon_{ls}=0.1$ 값으로 라벨 스무딩을 적용했다. 이러한 방법은 모델의 Perplexity를 악화시키지만 모델이 더 확신을 갖지 않도록 학습하면서 정확도와 BLEU 점수를 향상 시킨다. 여기서 Perplexity는 언어 모델에서 모델의 예측 불확실성을 측정하는 지표로서 값이 낮을수록 모델이 예측을 잘한다는 의미이다.
6. Results
6.1 Machine Translation
WMT 2014 영어-독일어 번역 작업에서 big 트랜스포머 모델은 이전에 보고된 최고의 모델들 (앙상블 모델 포함)을 BLEU 점수에서 2점이상 능가하며 최고 BLEU 기록인 28.4를 기록했다. 이 모델의 구성은 표3의 가장 아래 줄에 나와있다. 학습은 8개의 P100 GPU를 활용해 3.5일 동안 진행되었다. 심지어 기본 모델도 이전에 발표된 모든 모델과 앙상블 모델을 능가하며, 경쟁 모델의 학습 비용에 비해 훨씬 적은 비용으로 성과를 낸다.
WMT 2014 영어-프랑스어 번역 작업에서, 우리가 만든 big 트랜스포머 모델은 41.0의 BLEU 점수를 기록하며, 이전에 발표된 모든 단일 모델들을 능가한다. 또한 이전 최첨단 모델의 훈련 비용보다 1/4 이하의 비용으로 훈련되었다. 영어-프랑스어 번역을 위한 big 트랜스포머 모델은 드랍아웃 비율은 0.3대신 $P_{drop}=0.1$을 사용했다.
기본 모델의 경우 체크포인트를 10분 간격으로 기록해, 10분마다 한번씩 모델의 상태(가중치, 옵티마이저 상태 등)를 저장했다. 마지막 5개의 체크포인트를 평균화하여 하나의 단일 모델을 생성했다. 큰 모델의 경우, 마지막 20개의 체크포인트를 평균화해서 구했다. 우리는 검색 알고리즘으로는 빔 서치(beam search)을 사용했으며, 빔 크기는 4로 설정하고 길이 패널티 $\alpha = 0.6$을 사용했다. 빔 서치는 시퀀스 생성 문제에서 가장 확률이 높은 시퀀스를 선택하는 방법이다. 이러한 하이퍼파라미터들은 개발 환경에서 실험 후에 선택되었다. 추론중 최대 출력 길이는 입력길이 +50으로 설정되었지만, 더 일찍 종료하는 것도 가능하다.
table 2는 우리 결과를 요약하고, 번역 품질과 학습 비용을 기존의 다른 모델 아키텍처들과 비교한다. 우리는 모델 학습에 사용된 부동 소수점 연산의 수에 학습 시간, 사용된 GPU 개수, 각 GPU의 지속적인 단 정밀도 부동소수점 연산 성능(sustained single-precision floating-point)에 대한 추정치를 곱하여 추정했다. sustained single-precision floating-point란 일정 시간 동안 지속적으로 처리할 수 있는 GPU의 최대 처리 용량을 의미한다. 컴퓨터에서는 숫자를 처리할 때, 부동 소수점(floating-point) 형식을 사용해서 실수를 표현하는데, 이때 단정밀도(single-precision)은 부동소수점 연산에서 32비트 형식을 사용하는 것을 의미한다. 그리고 sustained이라는 말은 “지속적인” 이라는 뜻인데, GPU는 이론적으로 매우 높은 성능을 발휘할 수 있지만, 실제 학습에서는 이론적인 최대성능과 실제 지속적으로 낼 수 있는 성능에는 차이가 있다. sustained performance는 GPU가 일정 시간 동안 안정적으로 제공할 수 있는 성능을 의미한다.
6.2 Model Variations
트랜스포머의 다양한 구성 요소의 중요성을 평가하기 위해, 우리는 기본 모델을 여러 방식으로 변경하고, 개발 세트 newstest2013에서 영어-독일어 번역 성능의 변화를 측정했다. 우리는 이전 섹션에서 설명한 바와 같이 빔 서치(beam search)를 사용했지만, 이 과정에서는 체크포인트 평균화는 사용하지 않았다. 그 결과를 table3에서 확인할 수 있다.
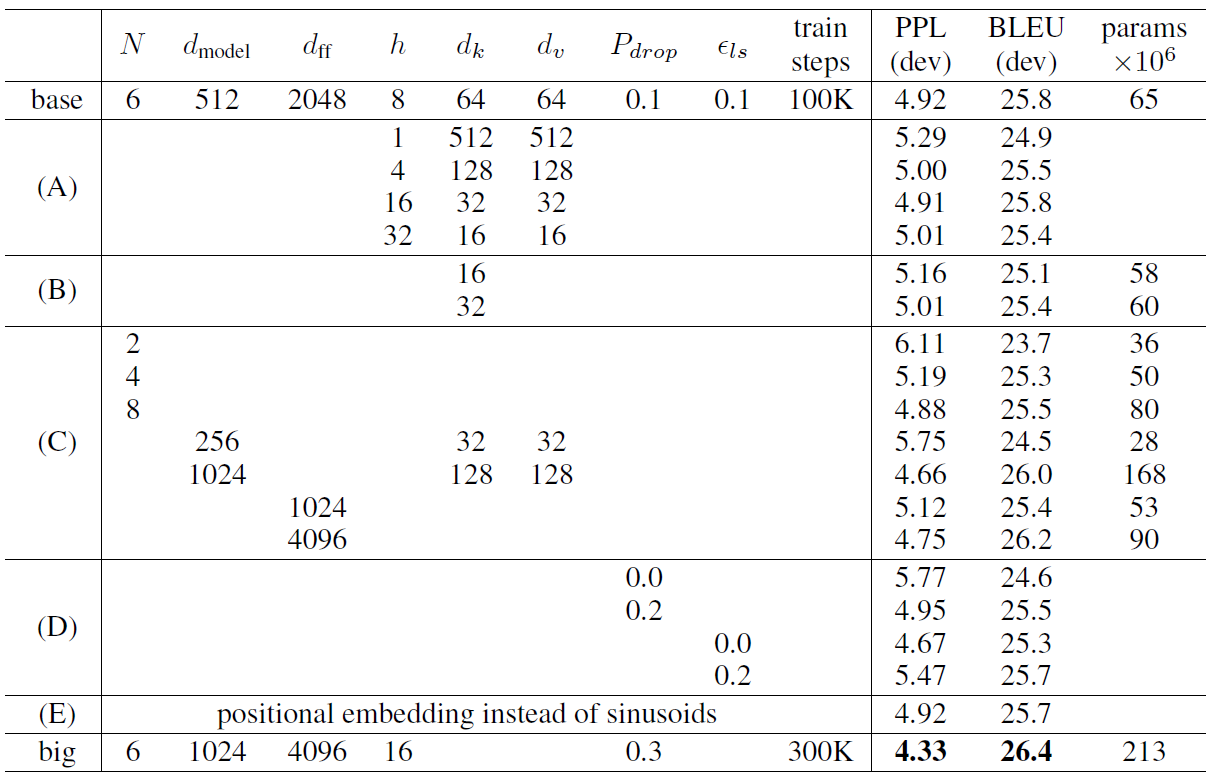
table3. 트랜스포머 아키텍처의 변형. 나열되지 않은 값들은 기본 모델(base model)과 동일하다. 모든 평가는 영어-독일어 번역 개발 세트인 newstest2013에서 수행되었다. 표에 나열된 perplexity는 바이트 쌍 인코딩에 따라 워드피스 단위로 계산되었으며, 단어 당 perplexity와 비교해서는 안된다.
table 3의 (A)행에서, 우리는 어텐션 헤드의 수와 어텐션 키 및 값의 차원을 변경했으며, 계산량은 일정하게 유지했다. 단일 헤드는 최적 설정 대비 BLEU 점수가 0.9 낮으며, 헤드 수가 너무 많아져도 품질이 저하된다.
table 3의 (B) 행에서 우리는 어텐션 키 크기($d_k$)를 줄이면 모델 품질이 저하된다는 것을 관찰했다. 이것이 시사하는 바는 호환성을 결정하는 것이 쉽지 않으며, 내적보다 더 정교한 호환성 함수가 유용할 수도 있음을 말한다. (C), (D) 행에서는 예상대로 더 큰 모델이 더 좋은 성능을 보였고, 드롭아웃이 과적합을 피하는데 매우 유용하다는 사실을 확인했다. (E)행에서는 사인파 기반 포지셔널 인코딩을 학습된 포지셔널 임베딩으로 교체했으며, 기본 모델과 거의 동일한 결과를 관찰할 수 있었다.
6.3 English Constituency Parsing
트랜스포머가 다른 작업에서도 뛰어난 성능을 보이는지 평가하기 위해, 우리는 영어 구문 분석(constituency parsing) 실험을 진행했다. 이 작업은 특정한 도전 과제를 제시하는데, 아웃풋은 강한 구조적 제약을 따르며, 아웃풋이 입력보다 훨씬 길다는 특징이 있다. 또한 RNN seq2seq 모델들은 데이터가 작은 환경에서 좋은 성능을 보이지는 않았다.
우리는 $d_{model}=1024$인 4개의 레이어로 구성된 트랜스포머에 Penn Treebank의 Wall Street Journal(WSJ) 데이터셋을 넣어 학습했으며, 이때 약 40,000개의 학습 문장을 사용했다. 또한 반지도학습(semi-supervised setting) 환경에서 이 모델을 학습했으며, 이때 고신뢰(high-confidence) 및 BerkeleyParser 데이터셋을 사용했으며, 약 1700만개의 문장을 포함했다. WSJ 데이터만 사용하는 환경에서는 16,000개의 토큰으로 구성된 어휘를 사용했으며, 반지도학습 환경에서는 32,000개의 토큰으로 구성된 어휘를 사용했다.
Table 4. 영어 구문 분석에 사용된 트랜스포머(WSJ의 섹션 23에 대한 결과)
| Parser | Training | WSJ 23 F1 |
|---|---|---|
| Vinyals&Kaiser el al.(2014) | WSJ only, discriminative | 88.3 |
| Pertrov et al.(2006) | WSJ only, discriminative | 90.4 |
| Zhu et al.(2013) | WSJ only, discriminative | 90.4 |
| Dyer et al.(2016) | WSJ only, discriminative | 91.7 |
| Transformer(4 layers) | WSJ only, discriminative | 91.3 |
| Zhu et al.(2013) | semi-supervised | 91.3 |
| Huang&Harper.(2009) | semi-supervised | 91.3 |
| McClosky et al.(2006) | semi-supervised | 92.1 |
| Vinyals&Kaiser el al.(2014) | semi-supervised | 92.1 |
| Transformer(4 layers) | semi-supervised | 92.7 |
| Luong et al.(2015) | multi-task | 93.0 |
| Dyer et al.(2016) | generative | 93.3 |
우리는 드롭아웃, 학습률, 그리고 빔 크기를 section 22 개발 세트에서 선택하기 위해 소수의 실험만 수행했으며, 다른 모든 하이퍼파라미터는 영어-독일어 기본 번역 모델에서 변경하지 않았다. 추론할때는 최대 출력 길이를 입력길이 + 300으로 증가시켰다. 우리는 WSJ만 사용하는 환경과 반지도 학습 환경 모두에서 빔 크기를 21로 $\alpha=0.3$으로 설정했다.
table 4의 결과는 특정 작업에 맞춘 세부적인 튜닝이 부족했음에도 불구하고, 우리의 모델이 놀라울 정도로 잘 작동한다는 것을 보여준다. 이는 RNNG(Recurrent Neural Network Grammar)을 제외한 모든 이전에 보고된 모델보다 더 나은 결과를 보여준다.
RNN seq2seq 모델과는 달리, 트랜스포머는 WSJ 학습 세트의 40,000개의 문장만으로 훈련했을 때도 Berkeley-Parser보다 더 나은 성능을 보여주었다.
7. Conclusion
이번 논문에서는 트랜스포머를 소개했다. 이는 어텐션 기반 최초의 시퀀스 변환 모델로, 인코더-디코더 아키텍처에서 가장 일반적으로 사용되던 순환 레이어를 다중 헤드 셀프 어텐션으로 대체했다.
번역 작업에서는 트랜스포머가 순환 레이어나 합성곱 레이어 기반 아키텍처보다 훨씬 빠르게 훈련될 수 있다. WMT 2014 영어-독일어 및 WMT 2014 영어-프랑스어 번역 작업 모두에서 우리는 최고의 성능을 달성했다. 영어-독일어 번역 작업에서는 우리 모델이 이전의 모든 모델(앙상블 모델 포함)을 능가했다.
우리는 어텐션 기반 모델의 미래에 대해 기대하고 있으며 이를 다른 작업에도 적용할 계획이다. 우리는 트랜스포머를 텍스트 이외의 입력 및 출력형태를 포함하는 문제로 확장할 계획이며, 이미지, 오디오 및 비디오와 같은 큰 입력 및 출력을 효율적으로 처리하기 위해 지역적(local), 제한된(restricted) 어텐션 메커니즘을 연구할 계획입니다. 생성 과정을 덜 순차적으로 만드는 것 또한 우리의 연구 목표중 하나이다.
우리가 학습과 평가에 사용했던 모델은 다음 url에서 확인할 수 있다. https://github.com/tensorflow/tensor2tensor





