[기초통계] 로지스틱 회귀분석 개념 정리
업데이트:
로지스틱 회귀분석 개념 정리
참고링크
로지스틱 회귀분석 정의 1
로지스틱 회귀분석(logistic regression)은 영국의 통계학자인 D.R.Cox가 1958년에 제안한 확률 모델로서 독립변수의 선형 결합을 이용하여 사건의 발생 가능성을 예측하는데 사용되는 통계기법이다.
위 정의에서 주목해야할 부분은 로지스틱 회귀분석은 사건의 발생 가능성을 예측하는데 사용된다는 것입니다. 사건의 발생 가능성은 곧 사건이 발생할 확률인데요. ‘확률’이니까 0과 1사이의 값이 나오겠죠? 이처럼 로지스틱회귀와 일반회귀분석의 차이점은 일반적인회귀분석은 종속변수로 올수있는 값의 제한이 없는데, 로지스틱회귀분석의 종속변수는 0과 1사이 처럼 종속변수로 올수있는 값이 제한적이라는 것입니다.
로지스틱 회귀분석 정의 2
로지스틱 회귀는 선형 회귀분석과는 다르게 종속변수가 범주형 데이터를 대상으로 하며, 입력 데이터가 주어졌을 때 해당 데이터의 결과가 특정 분류로 나뉘기 때문에 일종의 분류(classification)기법으로도 볼 수 있다.
위 정의에서 주목해야할 부분은 로지스틱 회귀는 종속변수가 범주형 데이터일 경우를 다룬다는 것입니다. 이런 특성은 로지스틱 회귀분석을 이용해 분류도 가능하다는 뜻이됩니다.
로지스틱 회귀분석 정의 3
흔히 로지스틱 회귀는 종속변수가 이항형문제(즉, 유효한 범주의 개수가 두개인 경우)를 지칭할 때 사용된다. 이외에 두 개 이상의 범주를 가지는 문제가 대상인 경우엔 다항 로지스틱 회귀(multinomial logistic regression) 또는 분화 로지스틱회귀(polytomous logistic regression)라고 하고 복수의 범주이면서 순서가 존재하면 서수 로지스틱 회귀(ordinal logistic regression)라고 한다.
로지스틱 회귀분석 정의 1,2,3의 관계
정의1,2,3을 정리하면 다음과 같습니다. 우선 일반적인 로지스틱회귀인 이항형문제라고 합시다. 이 경우, 종속변수가 0 또는 1 입니다. 이걸 예측관점으로보면 결과값이 0과 1사이의 값이 나오니 확률이라고 이해해서 발생할 확률을 예측한다고 볼수도있구요. 아니면 애초에 종속변수가 0, 1 뿐이니까 ‘분류’한다고 생각할수도 있습니다. 결국 같은 말인데, 어떻게 바라보냐에 따라 차이가 나타나는 것 같습니다. 로지스틱 회귀분석은 초기에는 의료분야에 적용되었고, 현재는 사회과학 분야에서도 많이 쓰입니다. 예를들어 한 사람의 수입, 직장, 과거에 얼마나 돈을 잘 갚았는지 등을 고려해 신용점수(credit-scoring)에 쓰이기도 합니다.
로지스틱 회귀분석 모델
로지스틱 회귀분석을 위해 $\pi(x)$라는 표기법을 사용할 건데요.
아래 식처럼 $\pi(x)$란 $p(Y=1|x)$, 즉, $x$가 주어졌을 때의 확률변수 $Y$가 1일 확률이라고 생각하시면 되겠습니다.
그리고 위에서도 언급되었지만 종속변수 $Y$ 는 이항범주형 변수(binary response variable)입니다.
| $ \pi(x) = P(Y=1 | X=x) = 1- P(Y=0 | X=x) $ |
로지스틱 회귀분석은 아래와 같습니다.
$ \pi(x) = \frac{exp(\alpha + \beta x)}{1 + exp(\alpha + \beta x)} $
위 식은 일반화 시키면 아래와 같이 변경가능한데요.
$ \frac{\pi(x)}{1-\pi(x)} = exp(\alpha + \beta_{1}x_{1} + \dots + + \beta_{p}x_{p})$
위 식을 보니 오즈(odds)가 생각나네요. 또한 양변에 로그를 취하면 아래와 같이 변합니다.
$ logit[\pi(x)] = log\frac{\pi(x)}{1-\pi(x)} = \alpha + \beta_{1}x_{1} + \dots + + \beta_{p}x_{p} $
위 식처럼 오즈에 로그를 취한, 즉 log odds를 logit 이라고 합니다. 이와 같은 결과는 아래의 과정을 거쳐서 얻어집니다. 부록을 참고 해주세요.
로지스틱 회귀곡선 의미
로지스틱 회귀분석에서 베타는 중요한 정보들을 가지고 있습니다. 우선 베타가 0보다 큰지 작은지에 따라 로지스틱 회귀곡선 형태가 바뀝니다. 아래 그림을 보시죠.
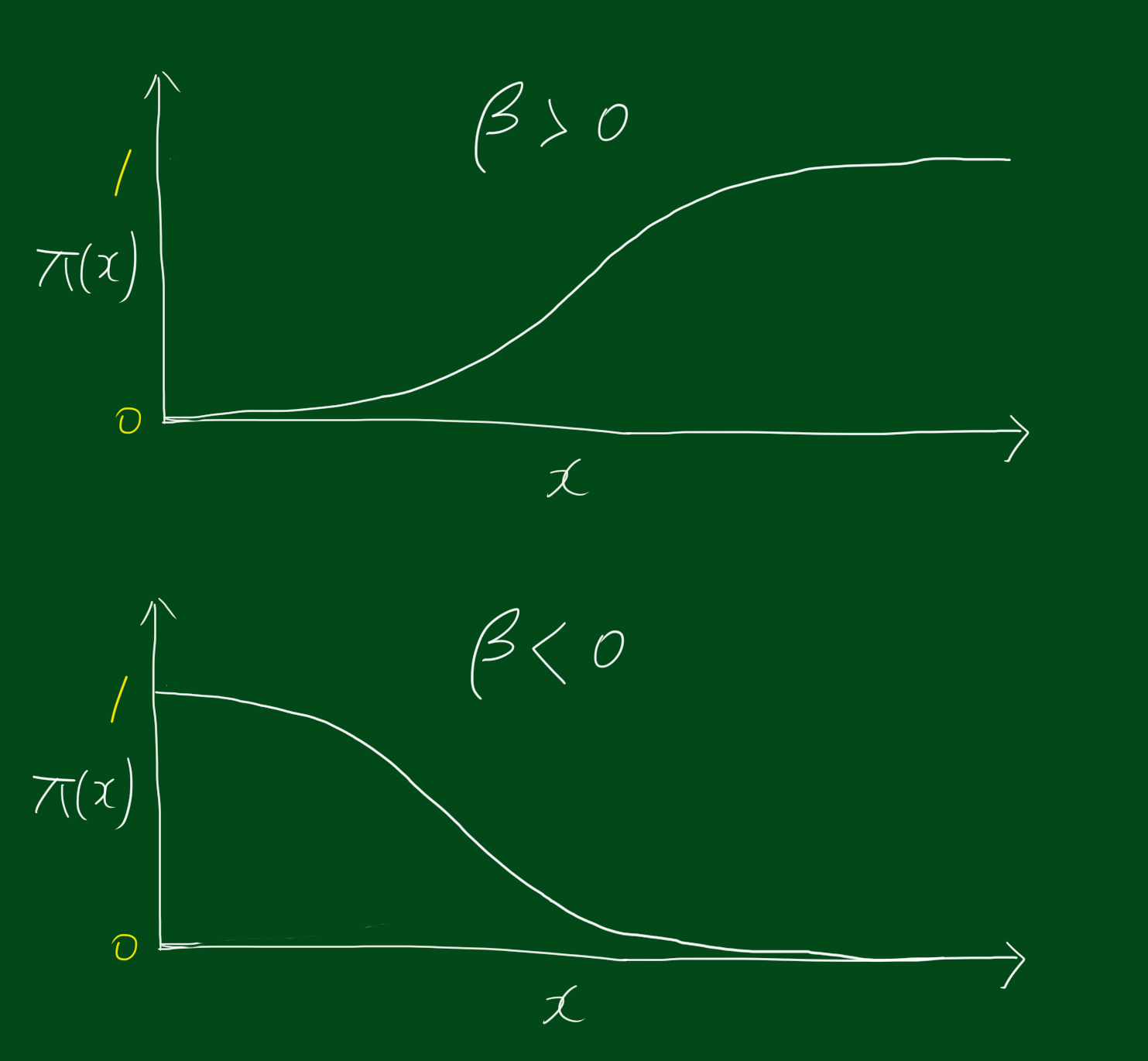
또한 로지스틱 회귀분석에서 베타는 회귀곡선의 기울기와 관련되어있는데요. 바로 독립변수 $x$가 한 단위 증가할 때 $\pi(x)$가 증가하는지 감소하는지를 나타냅니다. 아래 그림처럼 독립변수 $x$가 한단위 증가할 때 $\pi(x)$는 $\beta\pi(1-\pi)$ 만큼 증가합니다. 참고로 베타가 0에 가까울수록, 회귀곡선은 수평선에 가까워집니다.
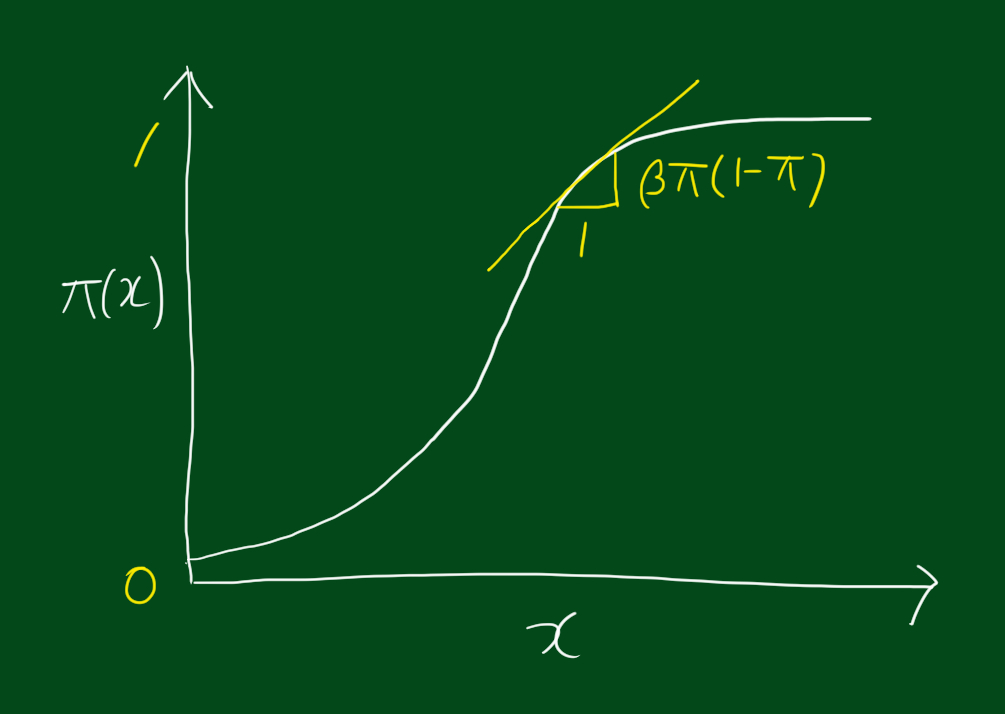
위 그림에서 기울기에 대해 이야기해봅시다. 위 곡선에서 $\pi(x)=1/2$ 일 때, $x=-\frac{\alpha}{\beta}$일때 기울기가 가장 가파릅니다. 이 때 가장 기울기가 가장 가파른 $x$, 다른말로하면 $x$에 대한 $y$의 확률이 1/2이 되는 지점인 $x=-\frac{\alpha}{\beta}$일 때를 median effective level이라고 부릅니다. 또한 위에서 $\beta\pi(1-\pi)$는 $\frac{\partial\pi(x)}{\partial x}$를 구함으로써 얻어집니다. 이는 아래 과정을 통해 얻어집니다. 부록을 참고해주세요.
로지스틱 회귀분석 결과 해석
기본적인 회귀분석과 마찬가지로 로지스틱 회귀분석에서도 $\beta$의 해석이 중요합니다. 여러분이 $\beta$값을 구했을 때 이 $\beta$값을 어떻게 해석해야할까요?
$x$가 한단위 증가할때, 오즈는 $e^{\beta}$ 만큼 곱해진다. The odds multiply by $e^{\beta}$ for every 1-unit increase in $x$
$\beta$는 위 문장처럼 해석되는데요. 위 문장에 따르면 $e^{\beta}$는 곧 ‘오즈비’입니다. 왜냐하면 아래와 같기 때문입니다.
$ e^{\beta} = \frac{odds(X=x+1)}{odds(X=x)} $
문장만보면 쉽게 이해되지 않을수도있으므로 예제를 들어보겠습니다. 아래와 같은 로지스틱 회귀모형이 있다고 가정합시다.
$ \hat{\pi(x)} = \frac{exp(-12.3+0.5x)}{1 + exp(-12.3+0.5x)} $
저 모형을 어떻게 해석해야할까요? 우선 50% 구간을 살펴보면 아래와 같이 $x=24.8$일 때, 추정된 확률이 50%라는 것을 알 수 있습니다.
$x = - \frac{\hat{\alpha}}{\hat{\beta}} = \frac{12.3}{0.5} = 24.8$
또한 $x$가 한 단위 증가할 때마다 오즈의 추정치는 $exp(\hat{\beta})=exp(0.5)=1.64$ 만큼 곱해집니다. 즉, $x$가 한 단위 증가할 때마다 오즈의 추정치는 64% 증가합니다.
부록