[머신러닝] 서포트 벡터 머신(support vector machine) 개념 정리
업데이트:
서포트 벡터 머신(support vector machine) 개념 정리
참고링크
개요
본 포스팅은 MIT강의를 참고했습니다.
데이터 셋을 classification 하는 방법에는 여러가지가 있습니다. 크게 선형(linear)방법과 비선형(nonlinear) 방법이 있는데요. 선형방법에 대표적인 방법에는 LDA(Linear Discriminant Analysis), 로지스틱회귀분석 등이 있고, 비선형방법의 대표적인 방법에는 오늘 다룰 서포트 벡터 머신(support vector machine)이 있겠습니다. 여기서 비선형이란 경계(boundary)가 비선형이라는 말입니다. 지금부턴 서포트벡터머신을 간단히 svm 이라고 부르겠습니다.

margin
margin은 svm에서 핵심적인 개념입니다. 한글로 번역하면 ‘여백’이라고 해야할까요. 이 여백이 중요한 이유는 데이터셋을 분리시킬때 집단간 간격이 가능한한 가장 넓어야하기 때문입니다. 참고로 어떤 데이터 포인트가 경계선에서 가능한 한 멀리있을수록 우리의 확신 정도는 강해집니다. 만약 어떤 점이 경계선 근처에 있다면 경계선이 바뀔 경우 해당 데이터포인트가 속하는 집단이 달라질 수 있겠죠. 반면 경계선에서 멀~리 떨어져있다면 경계선이 어떻게 바뀌던 데이터포인트가 속하는 집단이 달라질 가능성은 별로 없습니다.
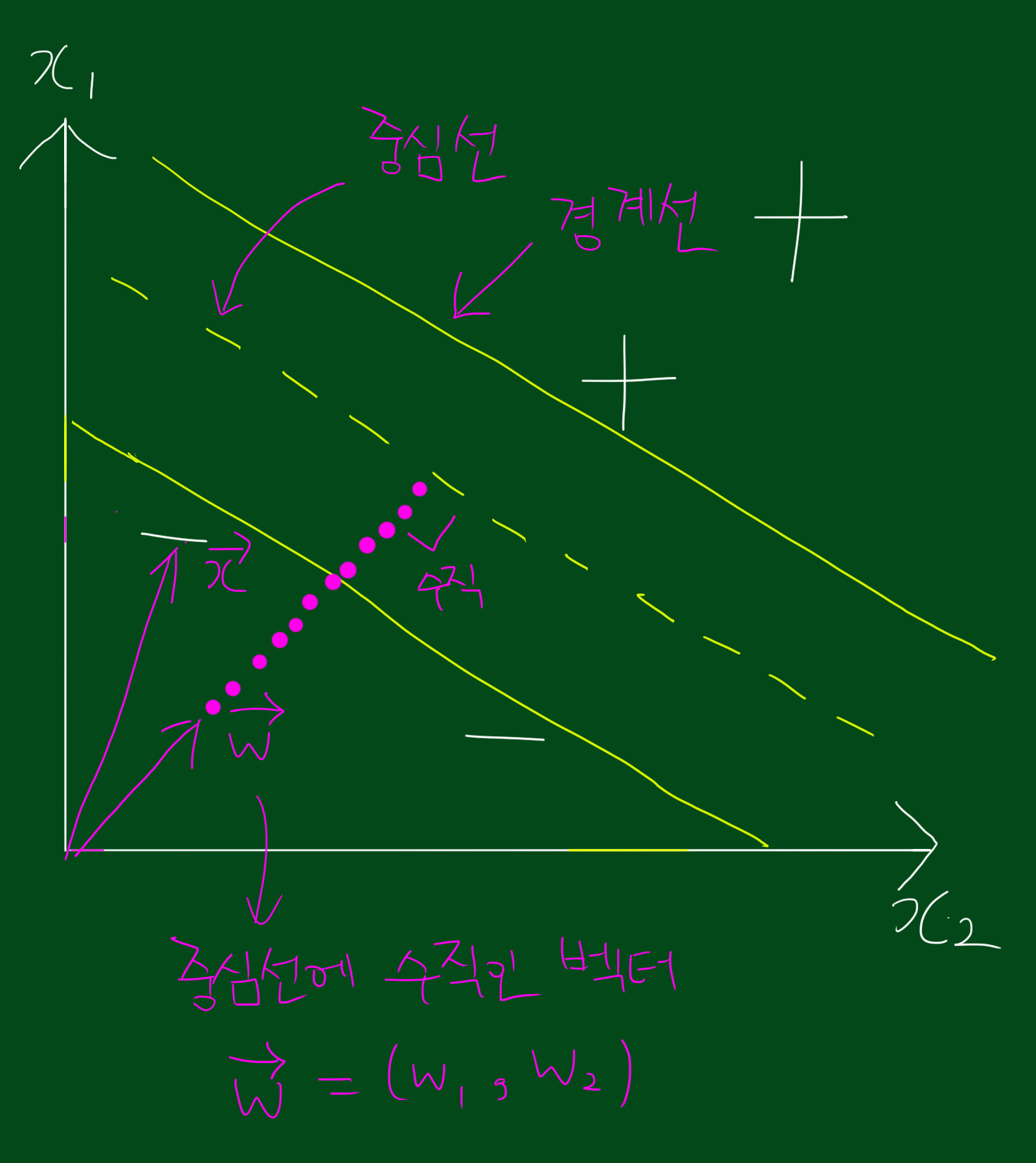
위 그림을 보시면 + 영역, - 영역, 중심선, 경계선이 있습니다. 그리고 중심선과 수직인 벡터 $\vec{w}$가 존재하는데요. 이 벡터 $\vec{w}$가 중요합니다. svm의 중심 아이디어는 각 데이터포인트 $(x_1, x_2)$과 $\vec{w}$를 내적시켰을 때, 즉, $(x_1, x_2)$과 $\vec{w}$을 내적한 값이 특정 상수 이상이면 +영역, 이하이면 -영역으로 정의할 수 있습니다.

이 때, 저희는 아직 $\vec{w} = (w_1, w_2)$와 $c$ 모두 알지 못합니다. 그리고 이것이 데이터분류를 위해 앞으로 저희가 구해야하는 값입니다.
decision rule

decision rule은 데이터의 분류를 위한 것입니다. 위 그림처럼 $\vec{w}$와 $\vec{x}의 내적값이 c보다 크면 +영역이고, c면 경계선, c보다 작으면 -영역입니다. 이를 일반화 시킨 것이 $\vec{w}\vec{x}+b \geq 0$인데요. 이제부터 $\vec{w}$와 $b$를 구해봅시다.

잠시 $\vec{w}$에 대해 생각해보면 사실 중심선에 직교하는 벡터는 굉장히 많습니다. 왜냐하면 위 그림처럼 벡터의 길이를 바꿀 수 있기 때문인데요. 그렇기 때문에 우리는 $\vec{w}$와 $b$를 구하기 위해서 추가적인 제약조건이 필요합니다.
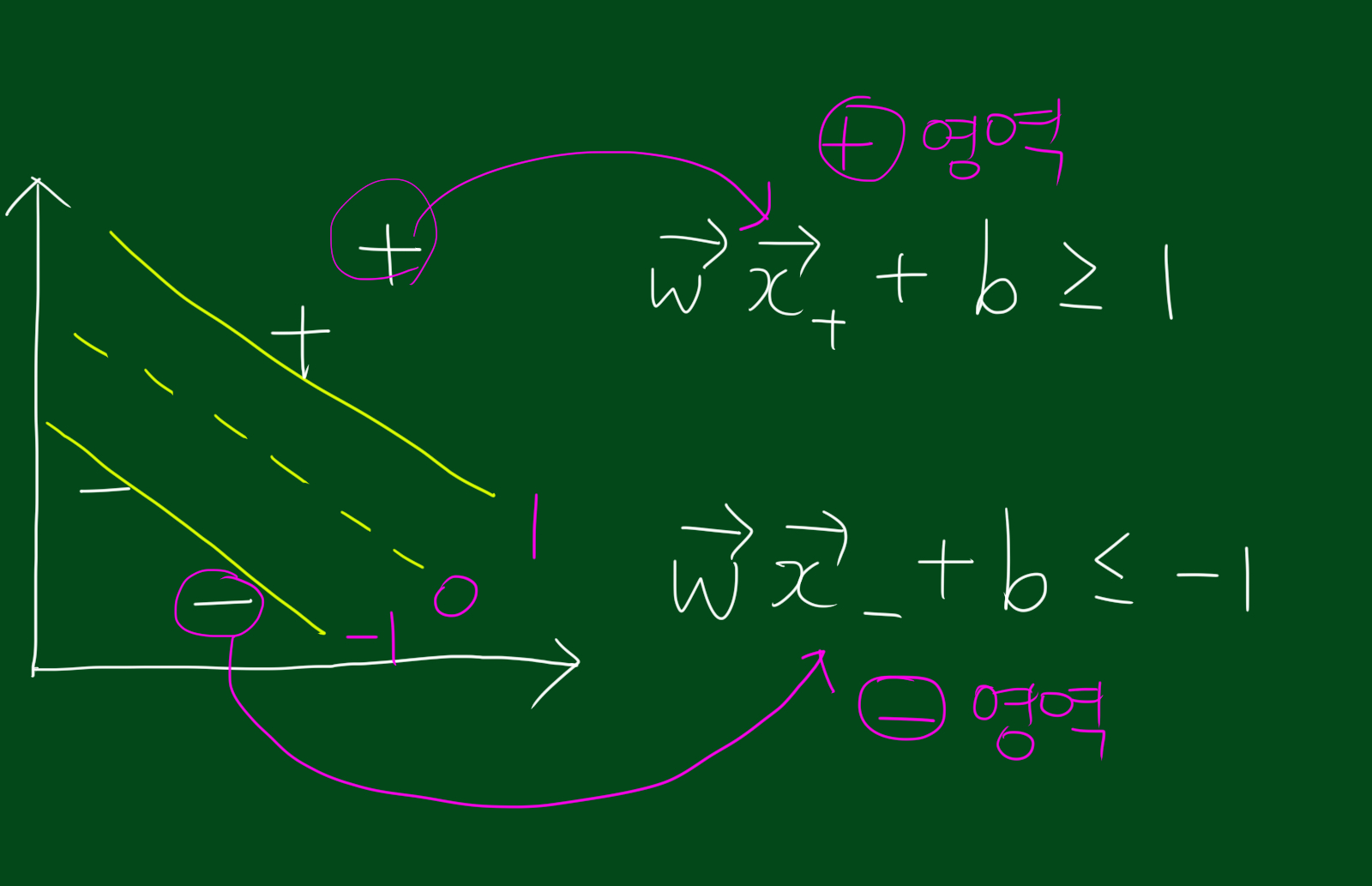
위 그림처럼 decision rule이 1보다 큰 영역을 +영역이라고 하고, -1보다 작은 영역을 -영역, 그리고 0인 곳이 중심선이라고 합시다.
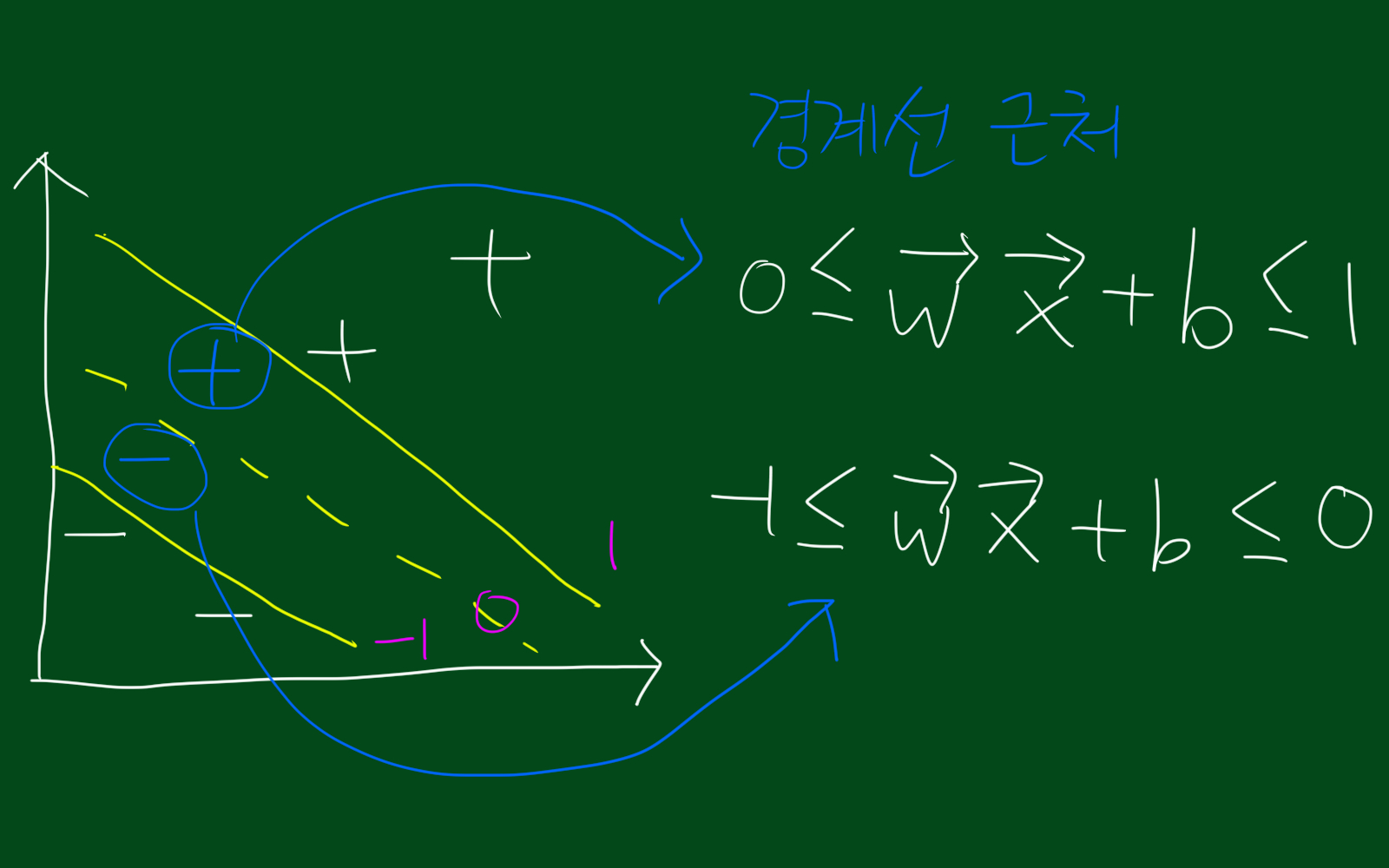
참고로 경계선과 중심선 사이의 값들은 위 그림 처럼 나타낼 수 있을 것입니다.
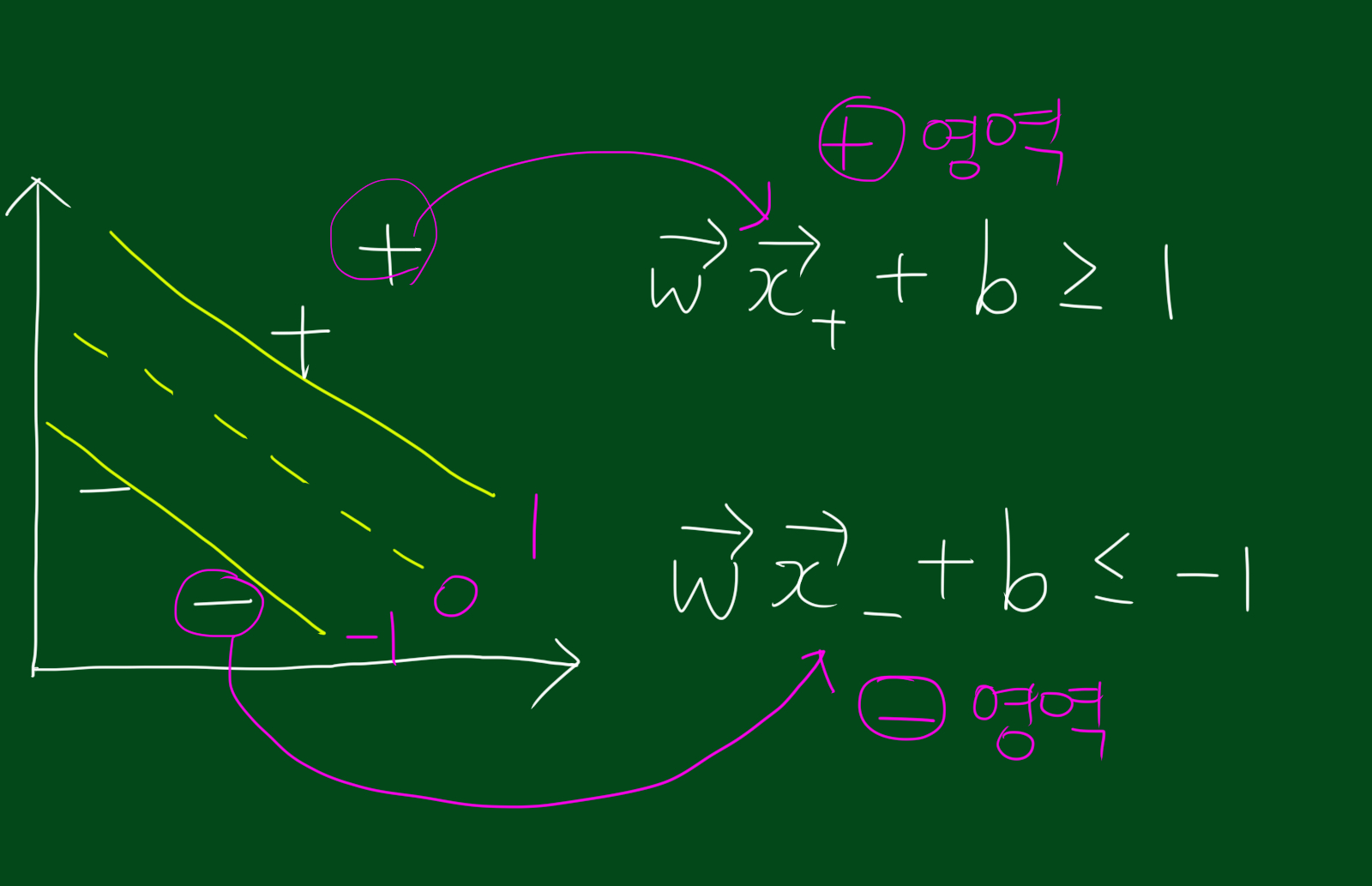
위 식에서 나온 식은 두 가지라 계산하기 불편한 부분이 있습니다. 두가지 식을 하나로 묶기 위해 $y_i$라는 새로운 변수를 도입합시다.
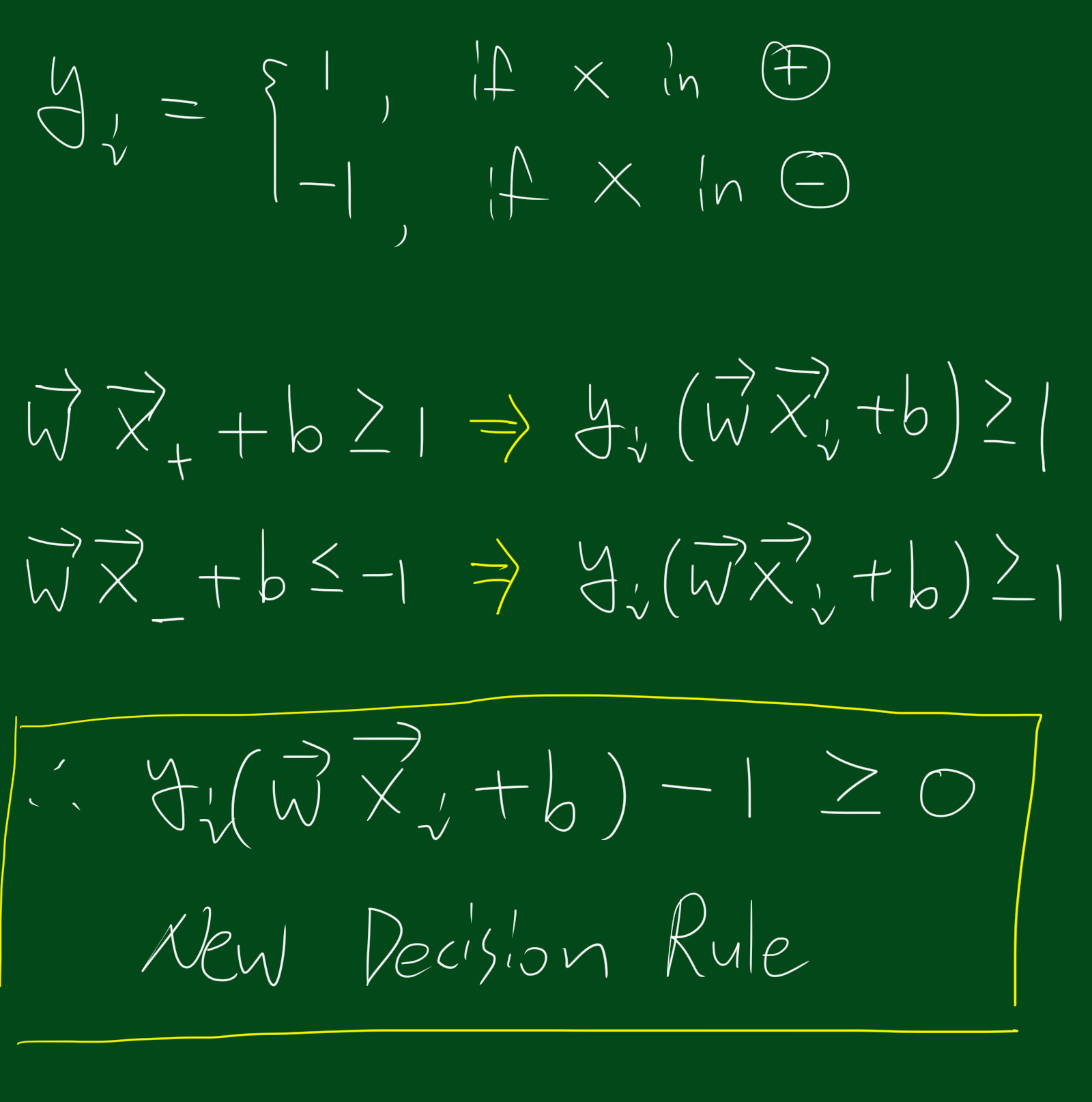
$y_i$는 쉽게 말하면 +영역에 속하면 1, -영역에 속하면 -1이라는 뜻입니다. 이 $y_i$를 이용하면 decison rule 두가지 식을 한가지로 묶을 수 있습니다.
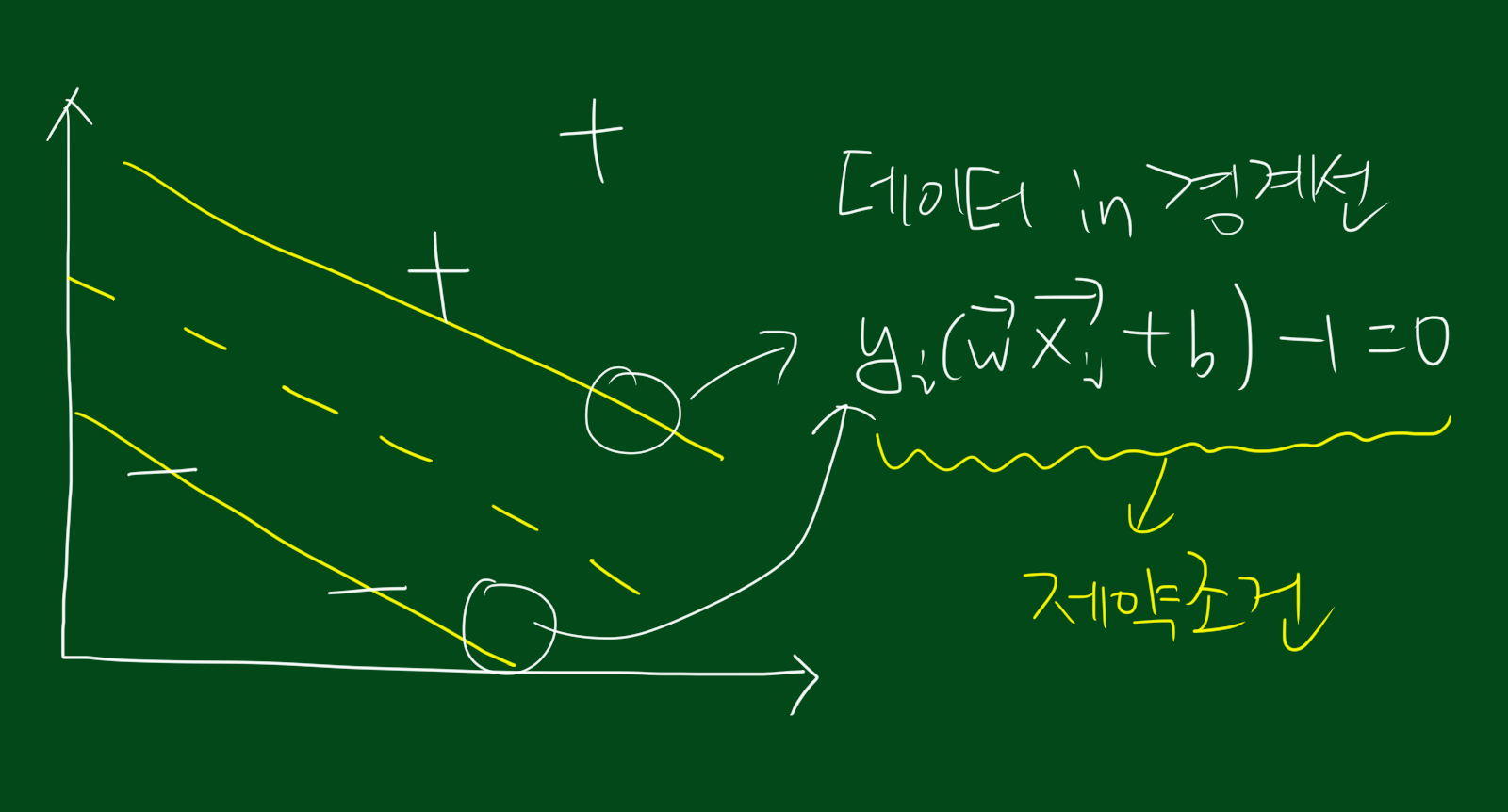
참고로 경계선에 데이터가 걸쳐있다면 위의 식이 성립됩니다. 위 식을 하나의 제약조건(constraint)이라고 보시면 되겠습니다.
너비(width) 최대화
위에서 말한 여백(margin)은 결국 직선 사이의 너비(width)를 최대화 시키는 것입니다. 너비를 최대화 시키기 전에 우선 너비가 얼마인지부터 구해야할것 같습니다.

위 그림처럼 경계선에 걸쳐있는 $\vec{x_{+}}$, $\vec{x_{-}}$의 차이벡터를 $\vec{w}$의 단위벡터에 내적시키면 너비를 구할 수 있습니다. 위 식에서 보면 너비는 결국 스칼라 값이고 우변의 내적값 또한 스칼라 임을 알 수 있습니다. 하지만 위 식을 바로 이용하기에는 복잡한 면이 있습니다. 위 식을 좀 더 쉬운 형태로 바꾸기 위해 아래 성질을 이용합시다.
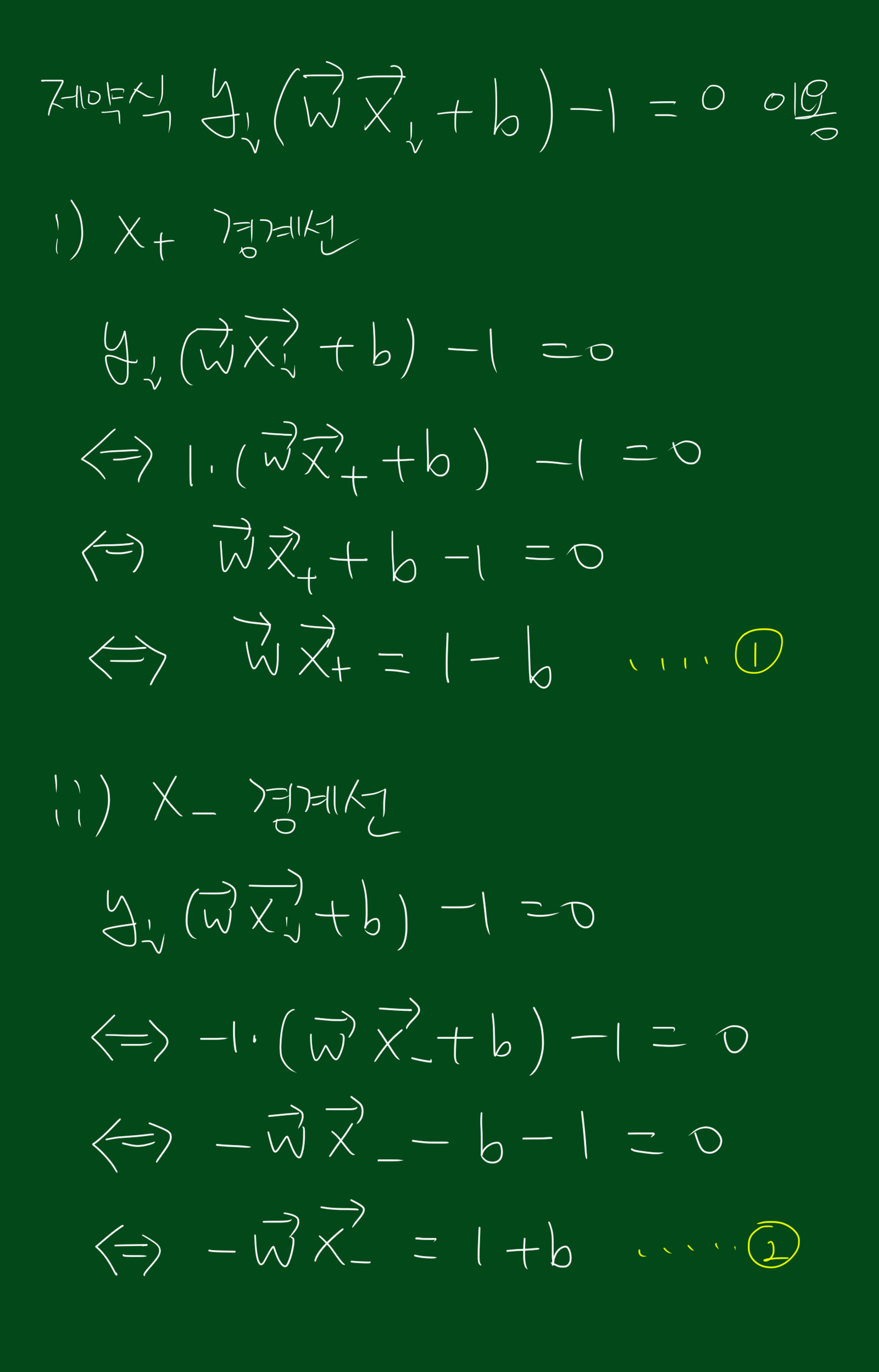
위 식을 이용해 너비구하는 식에 대입하면 아래와 같은 결과를 얻을 수 있습니다.
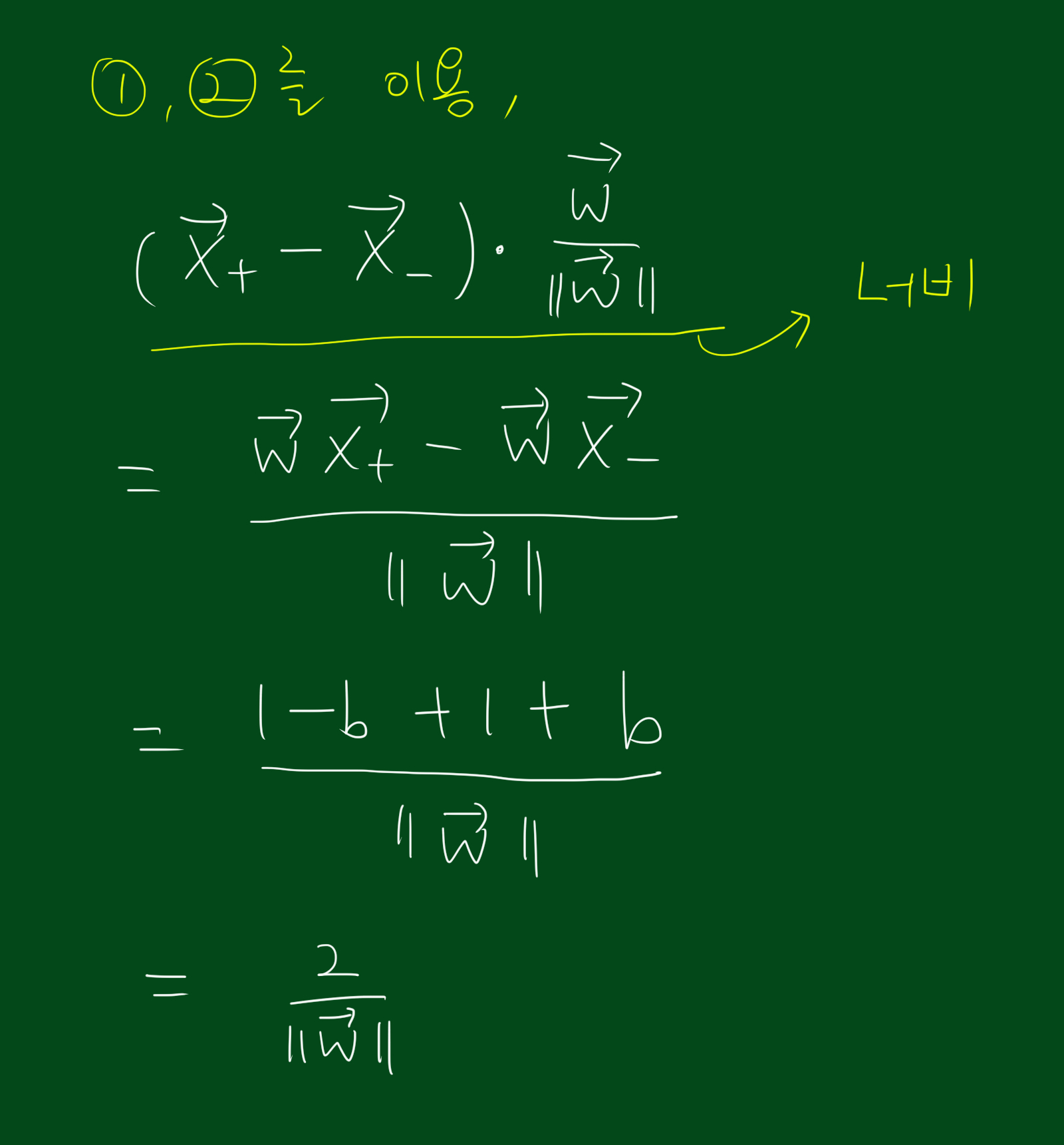
이제 너비 구하는 식이 좀 간단해 졌습니다. 결국 너비를 최대화 시키는 것은 아래식과 같습니다.
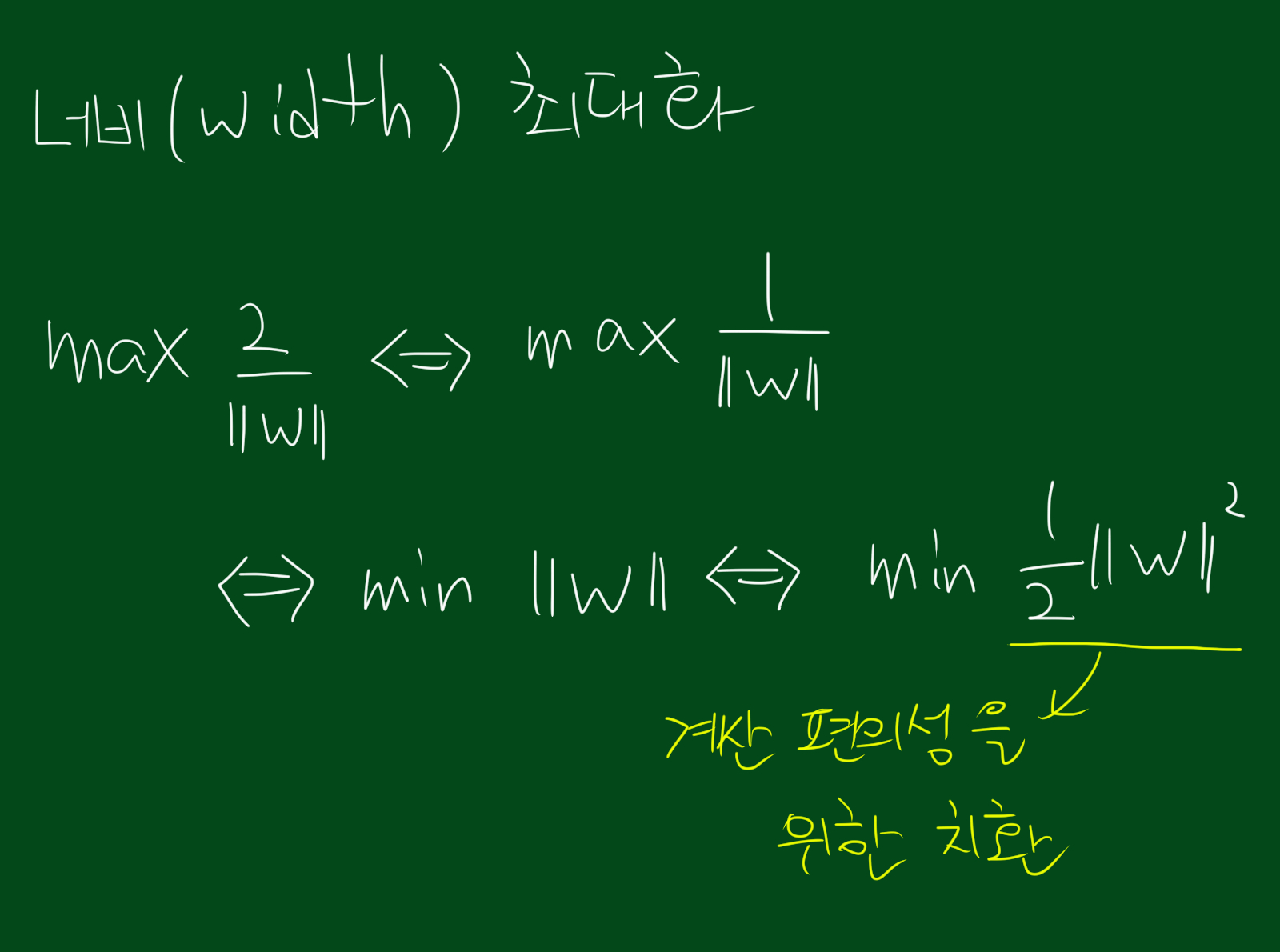
우리는 경계선에 관련된 제약식을 이용해 너비를 최대화 시켜야합니다.
어떤 제약식이 존재할때, 함수의 극한을 찾는 방법에는 라그랑주 승수법(Lagrange multiplier method)이 있는데요.
이를 사용하면 최소화 또는 최대화 할 새로운 식을 얻을 수 있습니다.
또한 최대화 시켜야할 식과 제약식을 합치는 형태이기 때문에 제한조건에 대해 생각하지 않아도 된다는 장점이 있습니다.
이렇게 합친 식이 아래 그림에서의 L과 같습니다.
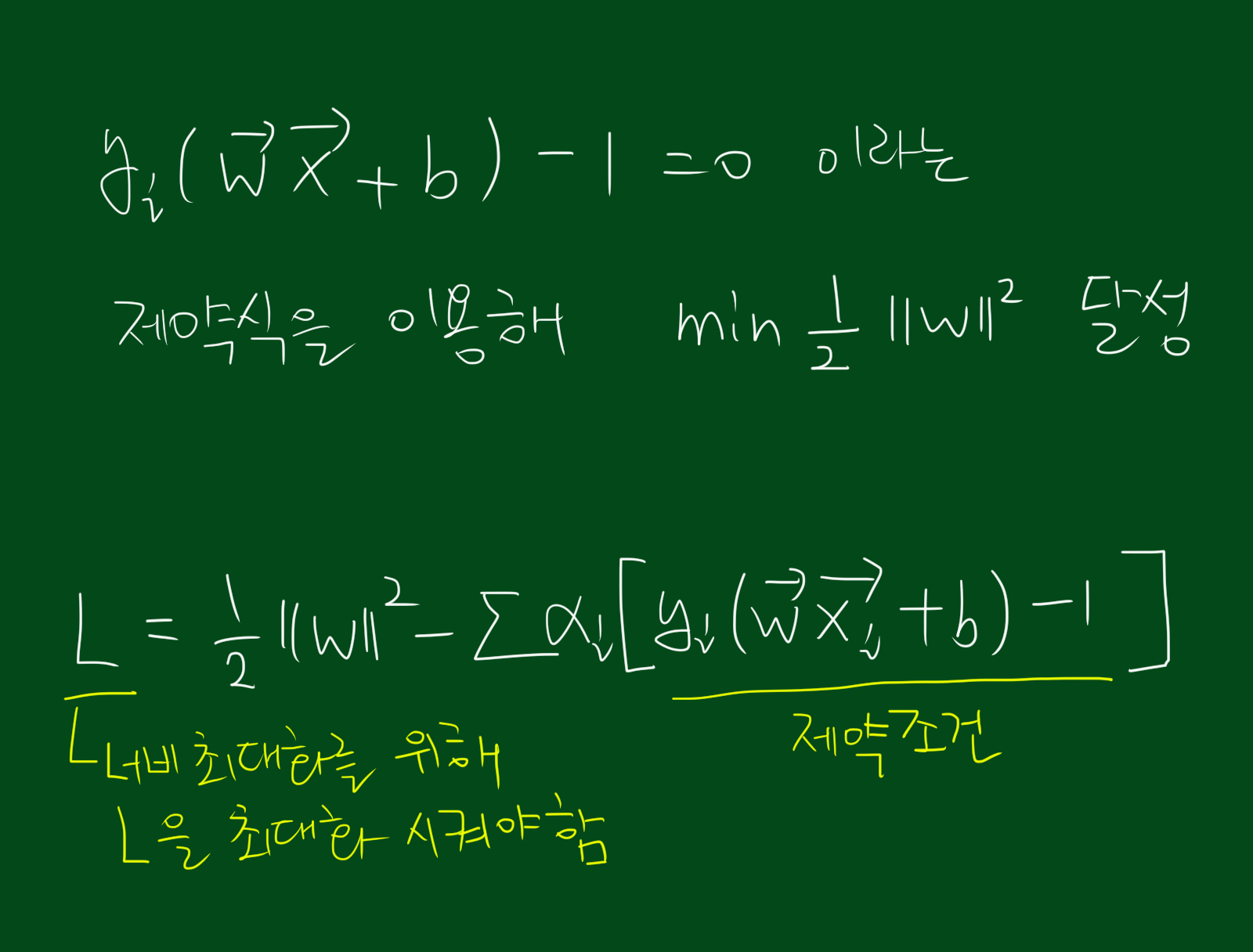
그리고 위 식의 L을 최대화 시키기 위해서는 우리가 구하고 싶은 $\vec{w}$, $b$에 대해 편미분해서 0이되는 지점을 찾아야합니다. (참고로 벡터의 미분은 스칼라의 미분과 성질이 같습니다.) 각 변수에 대해 미분한 값은 아래와 같습니다.
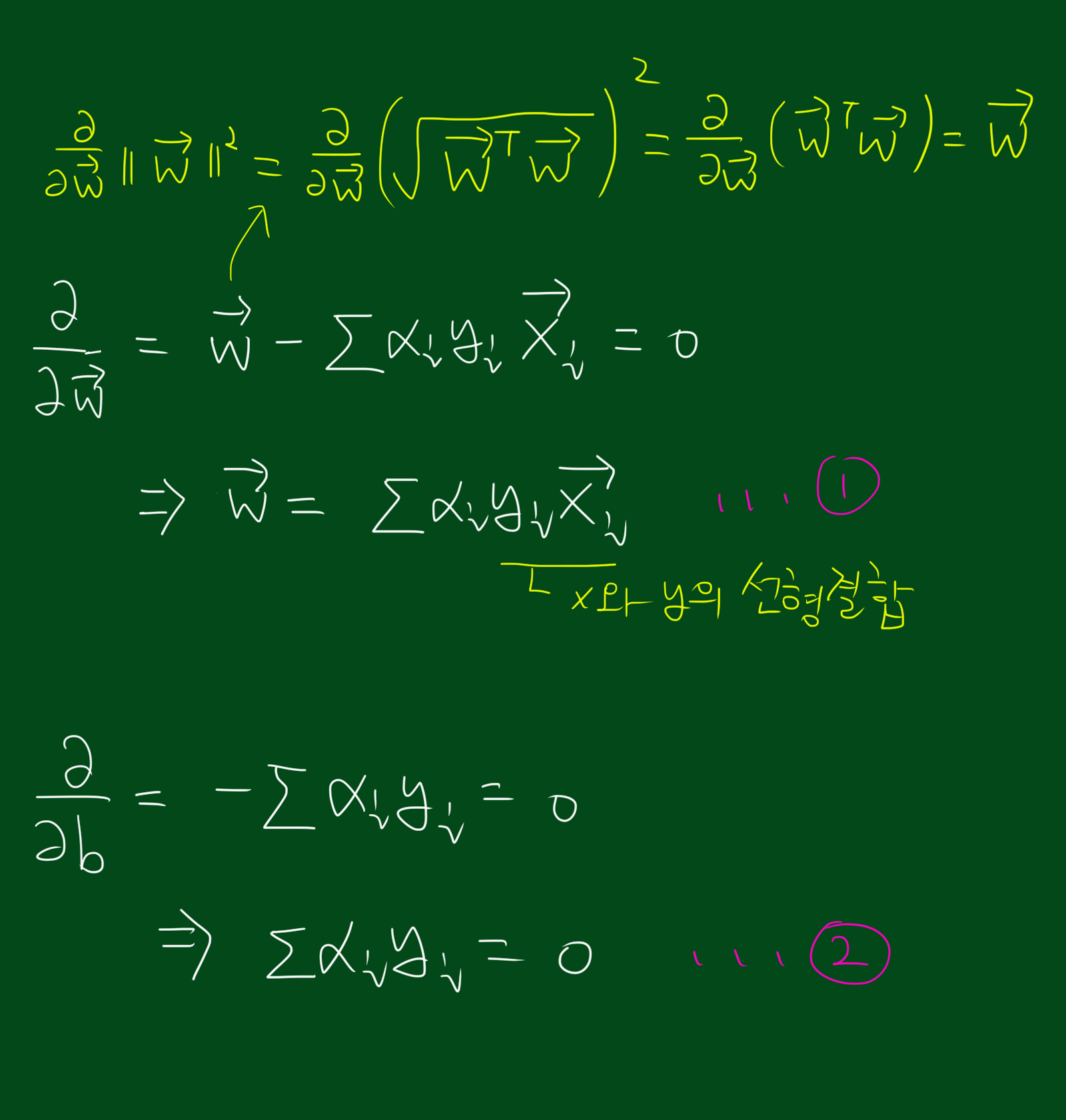
위 풀이로 도출된 2가지 식을 다시 L에 대입하면 다음과 같습니다. 아래 식을 잘 보시면 L을 최대화 시키는 데 영향을 끼치는건 오직 $\vec{x}$끼리의 내적 밖에 없다는 것을 알 수 있습니다.
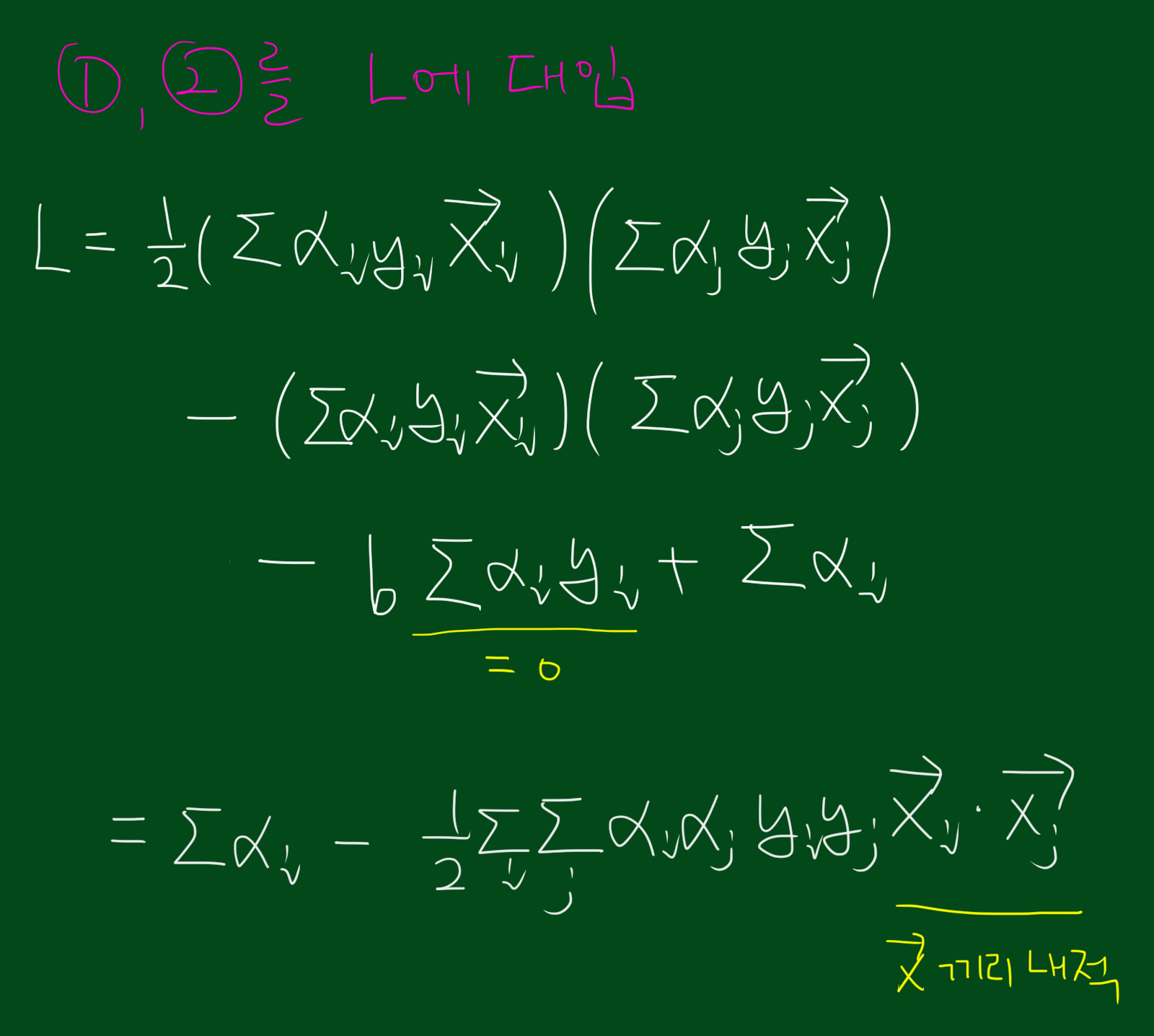
따라서 우리가 초반에 다루었던 Decision Rule은 지금까지 구한 식들과 조합하면 아래와 같이 바꿔 쓸 수 있습니다.
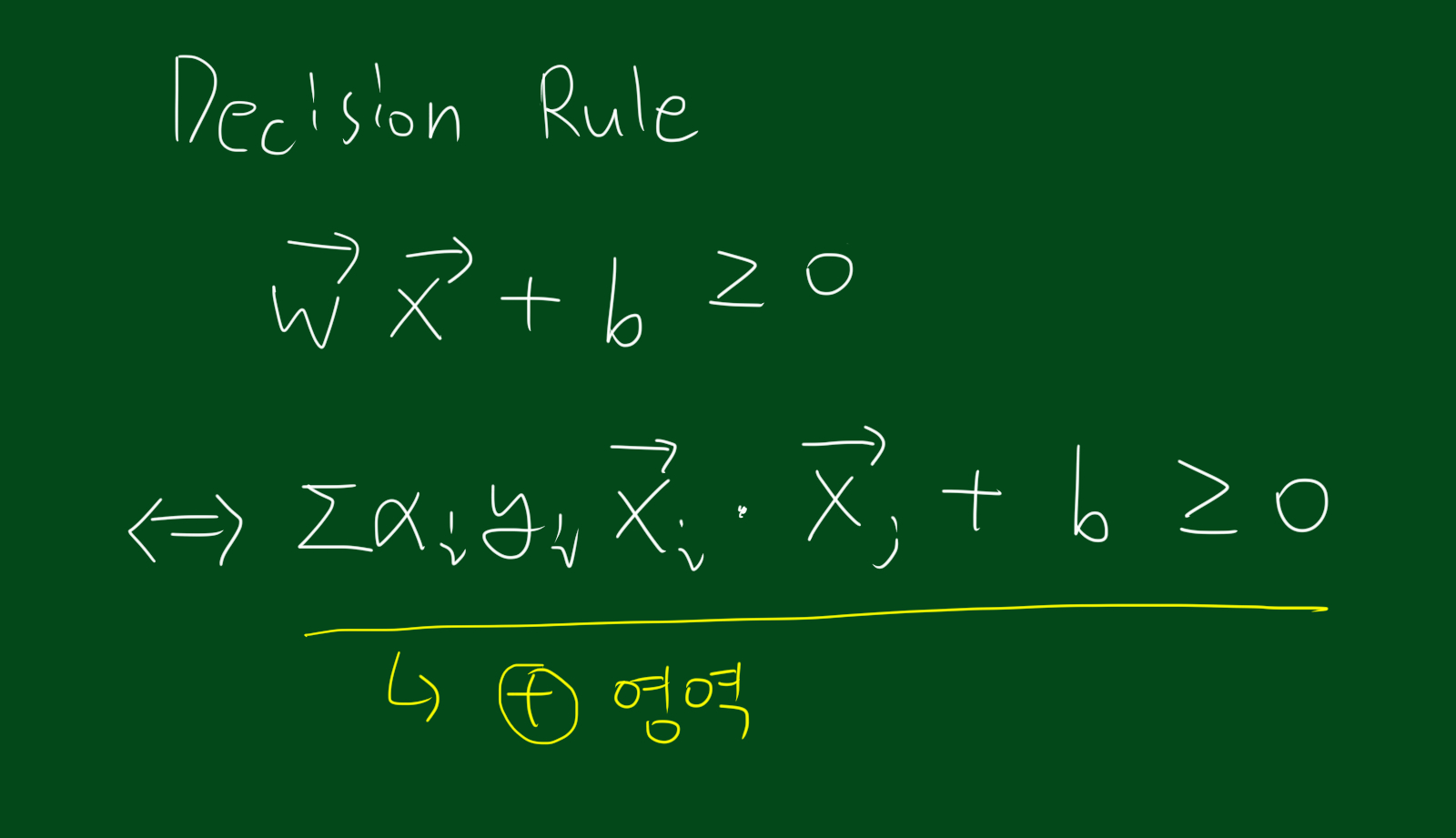
커널 함수 변경
우리는 지금까지 데이터를 직선형태의 구분벡터로 나누는 작업을 했습니다. 하지만 아래 그림처럼 선형으로 변형이 불가능할 때는 어떻게 할 까요?
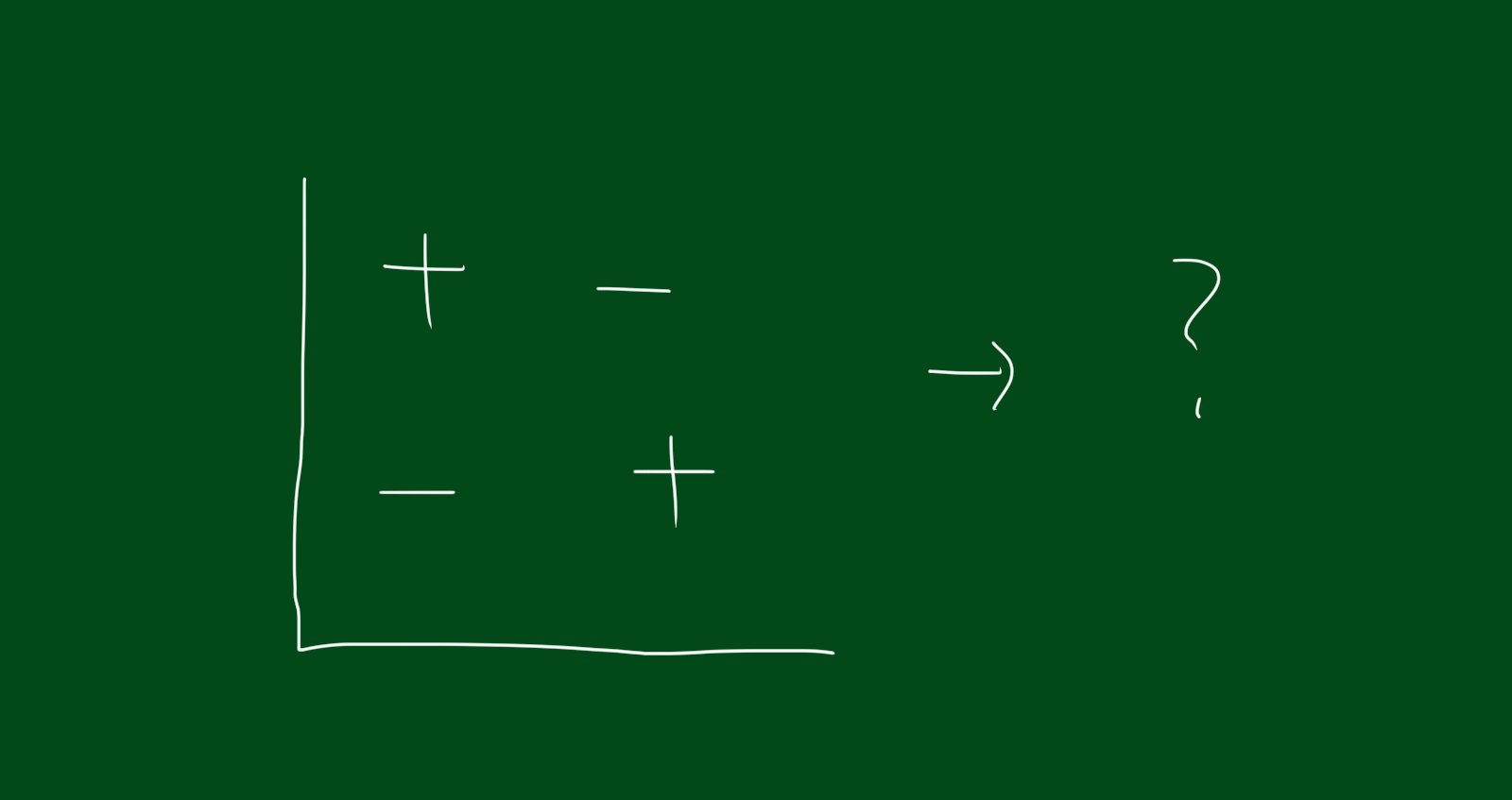
이때는 선형변환이 필요합니다. 즉, 데이터들이 뿌려져 있는 공간을 바꿔버리는 것이죠. 데이터들의 기저가 바뀌면 그에 따른 좌표도 바뀌게 됩니다.
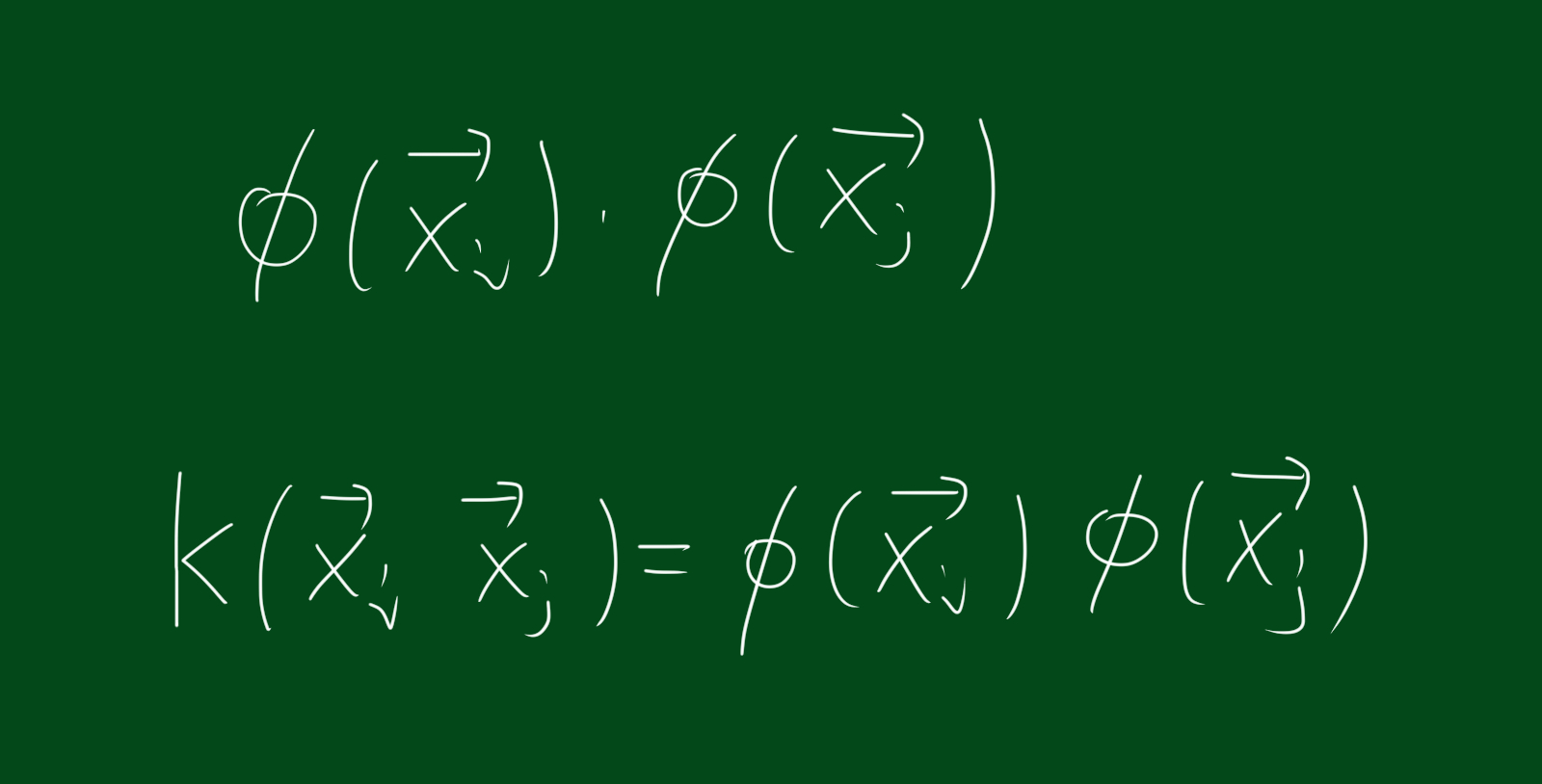
따라서 위 그림처럼 기존에 존재하는 $\vec{x}$벡터는 선형변환 함수 $\phi$를 거쳐 새로운 벡터 $\phi(\vec{x_i})$가 됩니다. 또한 L을 최대화시키는 식은 $\vec{x}$에만 의존한다고 했으므로 위 그림처럼 새로운 커널 함수는 $\phi(\vec{x_i})$와 $\phi(\vec{x_j})$의 내적꼴이 됩니다.
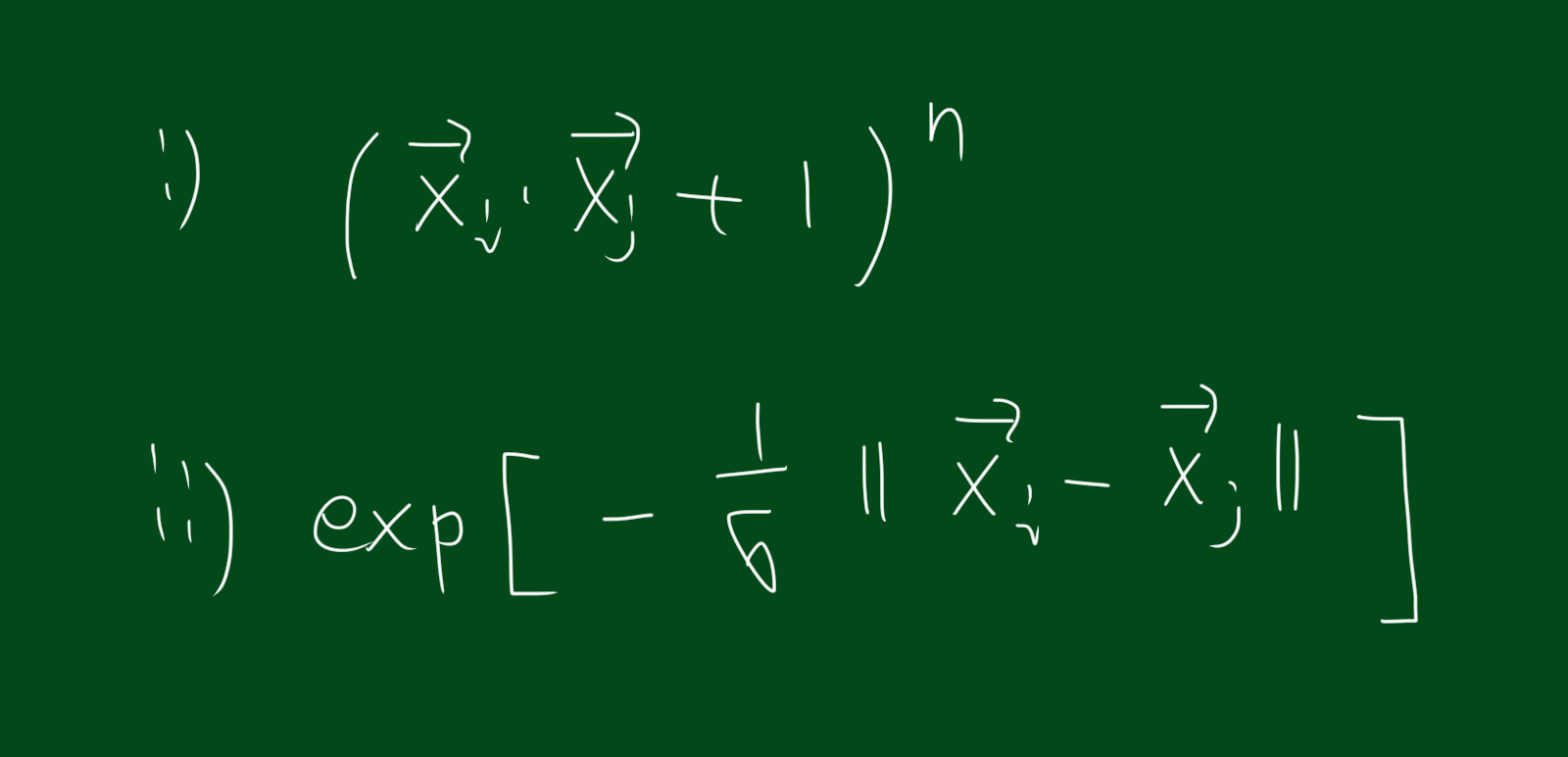
위 식은 유명한 커널 함수 입니다. 참고하시면 좋을 것 같아요.


