최대가능도추정(Maximum Likelihood Estimation) 개념 정리
업데이트:
최대가능도추정(Maximum Likelihood Estimation) 개념 정리
관련 링크
1. 최대가능도추정 정의
최대가능도추정은 얻어진 데이터를 토대로 그 확률변수의 모수를 구하는 방법이다. 어떤 모수가 주어졌을 때, 원하는 값들이 나올 가능도함수를 최대로 만드는 모수를 선택하는 방법이다.
위 정의에 따르면 최대가능도추정은 여러가지 모수 후보들 중 가능도함수를 최대로 만드는 모수를 사용해 실제 모수를 추정하는 것인데요. 최대가능도추정을 알기 전에 우선 가능도함수가 무엇인지 알아야겠습니다.
2. 가능도함수(likelihood function)이란
우리가 데이터를 요약할 때 평균이나 분산과 같은 여러가지 통계량을 사용하는데요. 가능도함수(likelihood function) 또한 데이터를 요약하는 데 사용됩니다. 가능도는 영어로 likelihood라고 하는데요. 보통 ‘그럴듯한’이라는 의미로 쓰입니다. 따라서 가능도함수를 쉽게 생각하면 ‘그럴듯한 함수’라고 생각하면 되겠네요. 그러면 무엇이 그럴듯할까요?
3. 가능도함수 정의
확률변수 $X=(X_1, X_2, \dots, X_n)$의 확률밀도함수를 $f(x|\theta)$ 라고 하겠습니다. 그리고 $X=x$가 주어졌을때, 가능도함수는 아래와 같이 정의 됩니다.
| $ L(\theta | x) = f(x | \theta) $ |
가능도함수는 모수가 $\theta$일 때, 주어진 표본 x가 얻어질 확률을 의미합니다. 이 때, 가능도함수는 $\theta$의 함수입니다. 주의하셔야 할 것은 $x$의 함수가 아니라는 것이죠. 왜일까요? $x$는 확률변수니까 가능도함수 또한 $x$의 함수여야 하지 않을까요? 가능도함수 식 바로 윗 문장을 보시면 $X=x$가 주어졌다고 나와있습니다. 즉, 확률변수 $X$는 주어졌으니(given) 더 이상 변수가 아닌거죠. 따라서 가능도함수에서 $x$는 정해졌으니 상수취급하는것이고 $\theta$값에 의해서만 가능도함수가 달라지니 가능도함수는 $\theta$의 함수라고 할 수 있습니다.
4. 가능도함수값이 크다?
가능도함수는 $\theta$값에 따라 함수값이 달라집니다. 그렇다면 가능도함수가 크다는 말은 무슨뜻일까요? 가능도함수값이 크다는 말의 의미는 해당 $\theta$일 때의 해당표본 $x$가 수집될 확률이 높다는 뜻입니다. 만약 $\theta$ 후보들 중 $\theta_1$, $\theta_2$가 있다고 합시다. 만약 $L(\theta_1|x) > L(\theta_2|x)$라면, $\theta_1$이 $\theta_2$보다 모수일 확률이 높다는 것이겠죠.
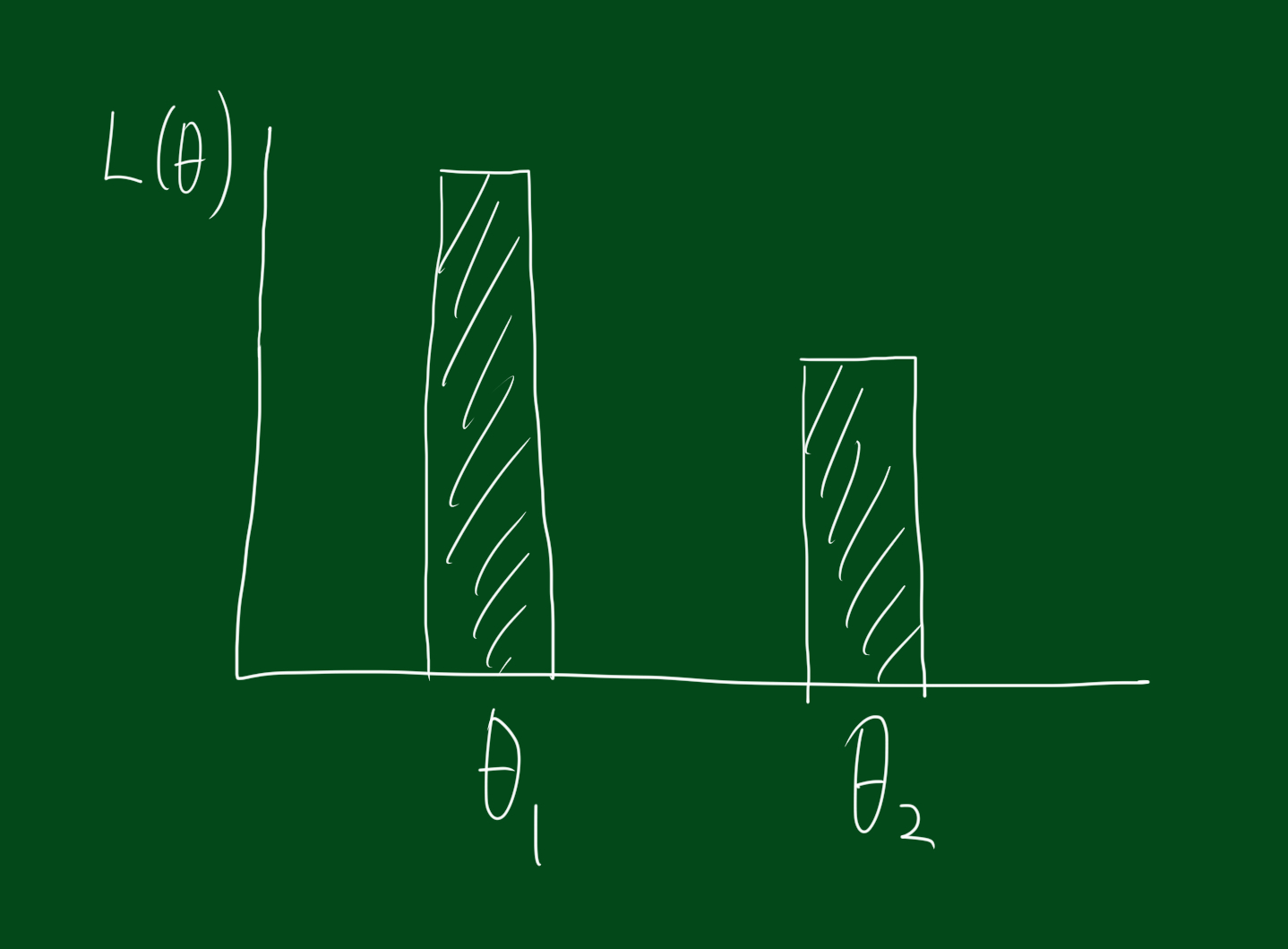
이를 그림으로 표현하면 위와 같습니다. 즉, $\theta_1$일 때 데이터 $x$가 수집될 확률이 높습니다. 따라서 가능도함수가 ‘그럴듯한 함수’인 이유는 해당 데이터가 수집되는 것이 ‘그럴듯하다’라는 뜻입니다.
5. 최대가능도추정
모수 $\theta$의 후보는 아주 많습니다. 따라서 최대가능도추정이란 모든 $\theta$ 후보들 중 가능도함수를 최대로 만드는 $\hat{\theta}$를 모수로 추정한다는 뜻입니다.
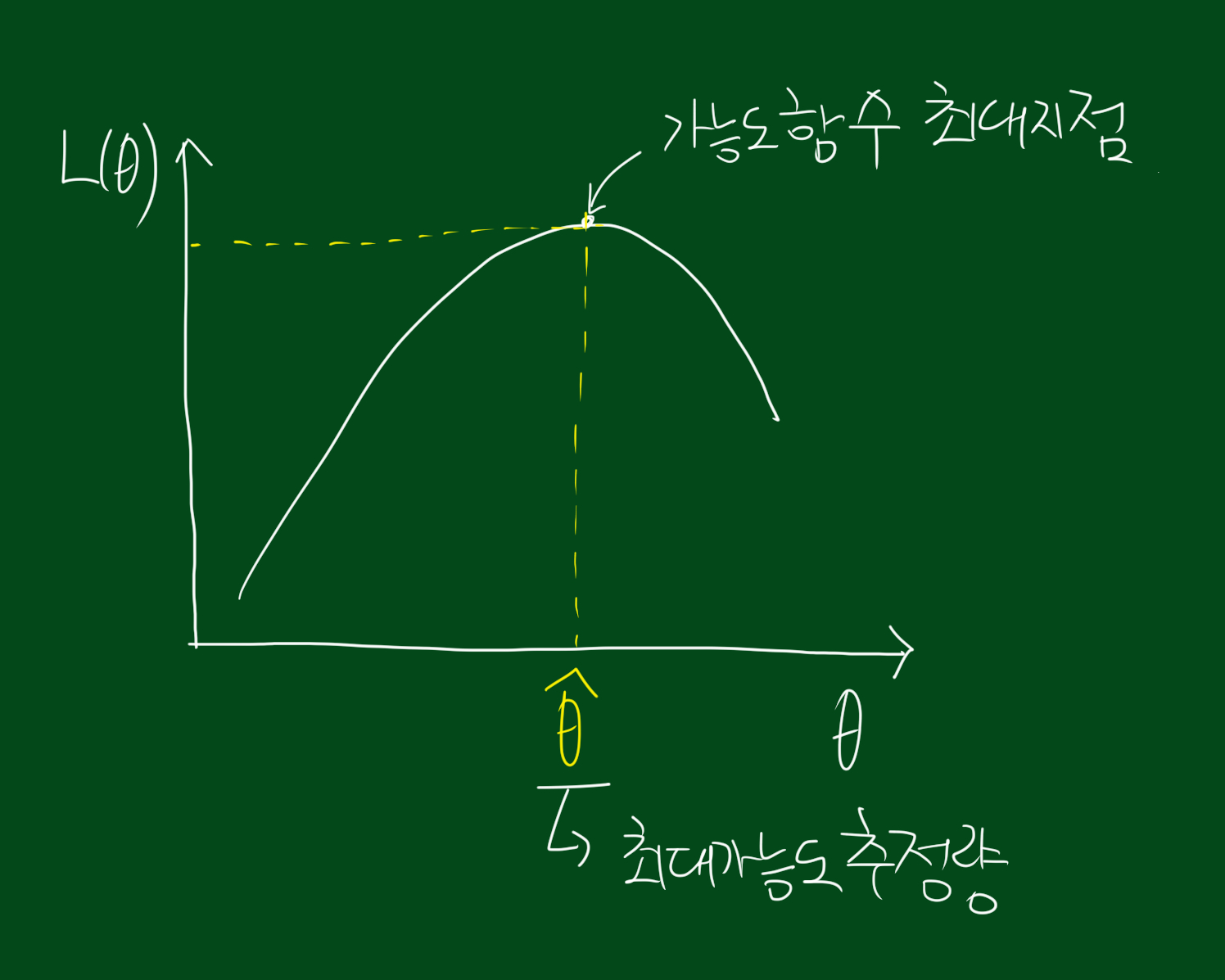
가능도함수에서 최대가 되는 $\hat{\theta}$를 찾으려면 두 조건을 만족해야합니다. 위 그림에서 알 수 있듯 극값이 되려면 한 번 미분해서 0이 되어야 하구요.
| $\frac{\partial}{\partial \theta}L(\theta | x) = 0$ |
첫째로 위 식을 만족해야합니다. 또한 최소값이 아닌 최대값이 되기 위해선 두번 미분한 값은 0보다 작아야합니다.
| $\frac{\partial^2}{\partial^2 \theta}L(\theta | x) < 0$ |
두번째로 위 식을 만족해야하는 것이죠. 위 두 조건을 만족하는, 즉, 최대가능도추정법을 이용해 구한 $\hat{\theta}$를 최대가능도추정량(maximum likelihood estimator)이라고 합니다.
끝으로 최대가능도추정의 정의를 다시한번 보면서 포스팅을 마치도록 하겠습니다.
최대가능도추정은 얻어진 데이터를 토대로 그 확률변수의 모수를 구하는 방법이다. 어떤 모수가 주어졌을 때, 원하는 값들이 나올 가능도함수를 최대로 만드는 모수를 선택하는 방법이다.
