[기초통계] 확률분포의 의미 및 종류

확률 분포의 의미 및 종류

참고링크

머신러닝	딥러닝	선형대수	기초통계	최적화
k-means	신경망이란	고유값,고유벡터	확률변수	컨벡스 셋
k-최근접이웃	성능함수	행렬식	확률분포	컨벡스 함수
선형회귀	신경망 학습	내적	모집단과 표본	라그랑주 듀얼
로지스틱회귀	교차연결	기저	평균과 분산	KKT 조건
릿지,라쏘회귀	합성곱 신경망	랭크, 차원	공분산, 상관계수	ROC 커브
의사결정나무	배치, 에포크 차이	선형변환	최대가능도추정	크로스 밸리데이션
서포트벡터머신	텐서플로기초(1)	직교행렬	베르누이,이항분포	실루엣 스코어
원클래스 SVM	텐서플로기초(2)	고유값분해	기하,음이항분포
LDA	seq2seq	특이값분해	초기하분포
GMM	opencv기초		포아송분포
부스팅	resnet		정규분포
사이킷런 실습	다각형내부판별		감마분포
	엣지판별		지수분포
			카이제곱분포
			베타분포
			균일분포

1. 확률 분포의 정의

확률분포(probability distribution)은 확률변수가 특정한 값을 가질 확률을 나타내는 함수를 의미한다.

위 정의를 이해하기 위해서는 확률변수와 함수라는 단어의 뜻을 알아야하는데요. 확률변수의 뜻은 이전 포스팅 참고 부탁드립니다. 또한 확률분포는 ‘함수’를 의미하는데요. 함수란 mapping을 의미합니다. 즉, 함수란 집합의 임의의 한 원소를 다른 집합의 한 원소에 대응시키는 관계를 의미합니다. 즉, 확률분포란 확률변수가 특정 값을 가질 확률이 얼마나 되느냐를 나타내는 것입니다.

확률 분포는 확률 변수의 종류에 따라 이산확률분포와 연속확률분포로 나뉘는데요. 쉽게 말해 확률변수를 셀 수 있는지 없는지에 따라 나눈다고 생각하시면 됩니다.

2-1. 이산확률분포

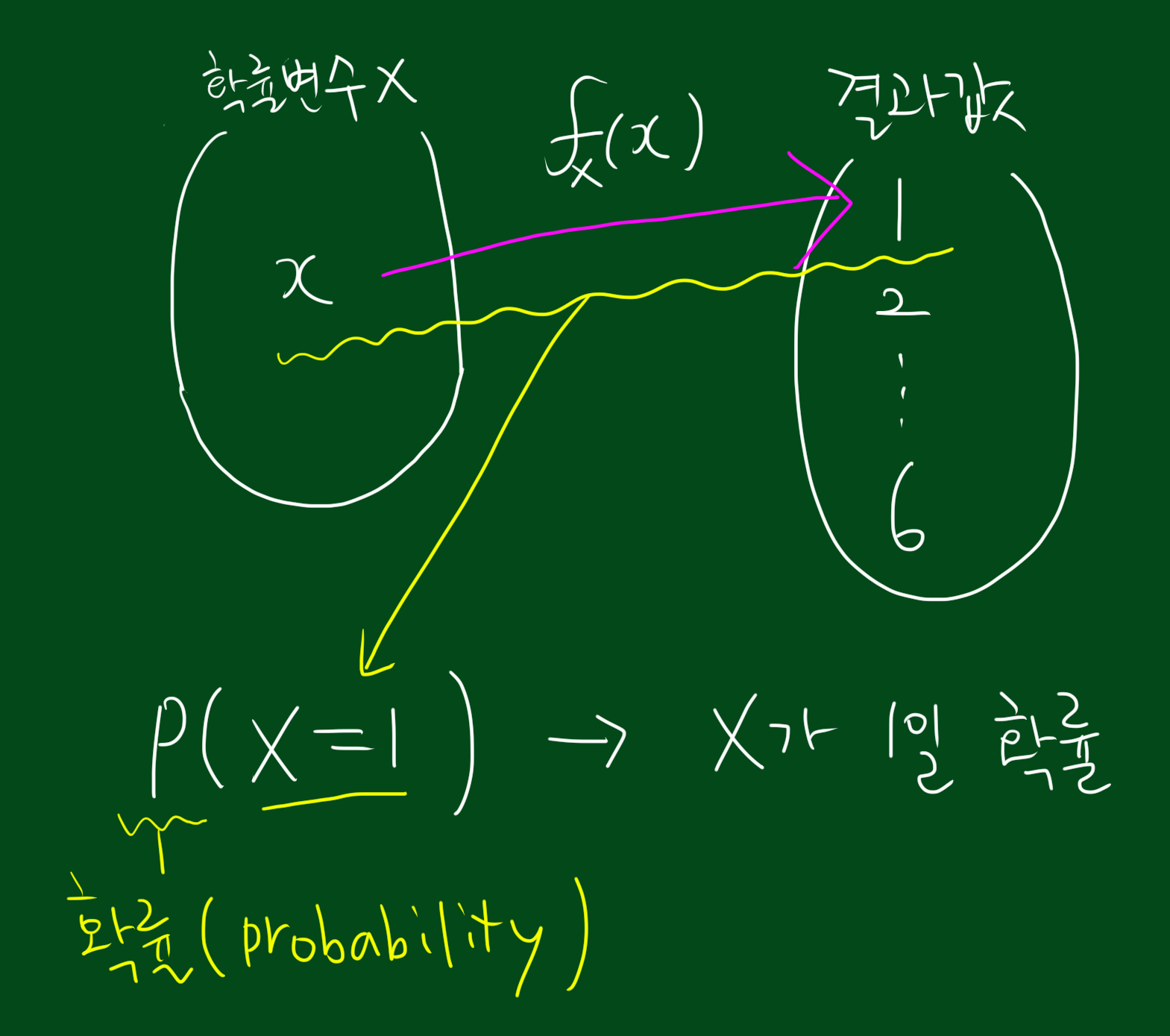
이산확률분포(discrete probability distribution)는 이산확률변수의 확률분포를 의미합니다. 여기서 이산확률변수는 확률변수가 가질 수 있는 값의 개수를 셀 수 있다는 의미입니다. 예를 들어, 확률변수 X를 주사위를 던져서 나오는 눈의 개수라고 하면 X는 1,2,3,4,5,6 여섯가지 경우를 가질 수 있습니다. 그리고 이 경우 확률변수가 가질 수 있는 값이 6개로 ‘셀 수 있는’ 경우 이므로 이산확률변수에 해당합니다.

2-2. 확률질량함수

확률질량함수(probatility mass function, pmf)는 이산확률변수에서 특정 값에 대한 확률을 나타내는 함수입니다.

즉 확률질량함수란 이산확률변수가 특정 값을 가질 확률을 의미합니다. 예를 들어 주사위를 던졌을 때 나오는 수를 X라고 하면 X가 1일 확률을 1/6이 된다는 것을 알 수 있습니다. 이를 수식을 나타내면 아래와 같습니다.

$ f_{X}(1) = P(X = 1) = 1/6 $

3-1. 연속확률분포

연속확률분포(continuous probability distribution)은 연속확률변수의 확률분포를 의미합니다. 여기서 연속확률변수는 확률변수가 가질 수 있는 값의 개수를 셀 수 없다는 의미입니다. 예를 들어, 확률변수 X를 중학교 1학년 학생의 평균 키라고 했을 때, X는 키이므로 실수값을 가지며 이는 ‘셀 수 없는’ 경우에 해당합니다. 따라서 이 경우 확률변수 X는 연속확률변수에 해당한다고 할 수 있습니다.

3-2. 확률밀도함수

확률밀도함수(probability density function, pdf)는 연속확률변수가 특정 구간에 포함될 확률을 의미합니다.

확률밀도함수는 이산확률분포에서 확률 질량함수에 대응된다고 할 수 있습니다. 다만 확률밀도함수는 연속확률변수에 대응되기 때문에 특정값을 가질 확률은 0이 되므로 특정값을 가질 확률이 아닌 특정 구간에 포함된다고 표현합니다.

4. 누적분포함수

누적분포함수(cumulative distribution function, cdf)는 주어진 확률 변수가 특정 값보다 작거나 같은 확률을 나타내는 함수이다.

즉, 누적분포함수를 수식으로 나타내면 아래와 같습니다.

$ F_{X}(x) = P(X \in (-\infty, x)) $

독립항등분포(iid, independent and identically distributed)

두 개 이상의 확률변수를 고려할 때, 각 변수들이 통계적으로 독립(independent)이고, 동일한 확률분포를 가지고 있을때(identically distributed) 독립항등분포를 따른다고 하는데요. 실제로 독립항등분포라는 한글 쓰는 대신 iid라고 줄여서 부릅니다.

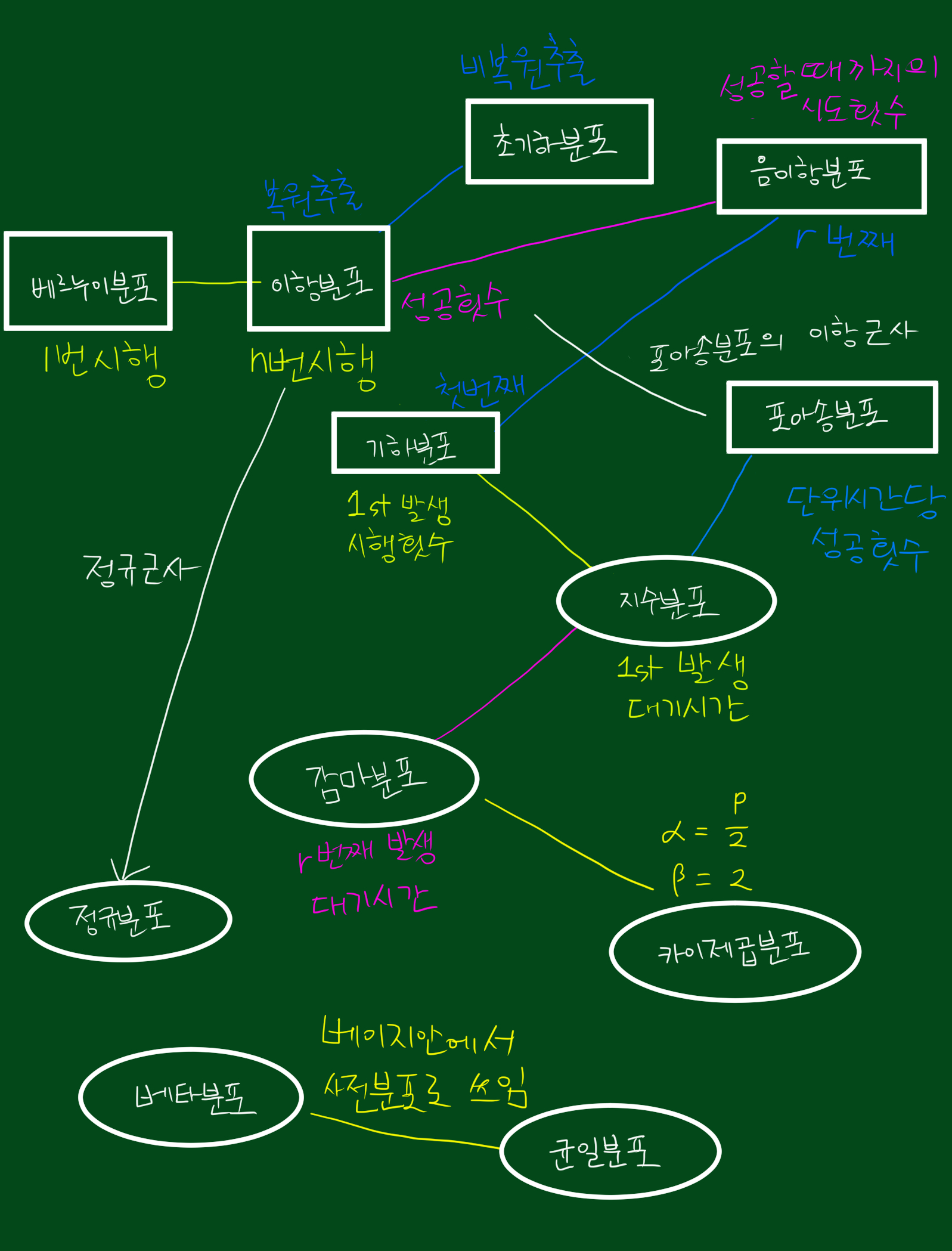
5-1. 이산확률분포의 종류

• 베르누이분포(Bernoulli Distribution)와 이항분포(Binomial Distribution)
• 기하분포(Geometric Distribution)와 음이항분포(Negative Binomial Distribution)
• 초기하분포(Hypergeometric Distribution)
• 포아송분포(Poisson Distribution)

5-2. 연속확률분포의 종류

• 정규분포(Normal Distribution)
• 감마분포(Gamma Distribution)
• 지수분포(Exponential Distribution)
• 카이제곱분포(Chi-squared Distribution)
• 베타분포(Beta Distribution)
• 균일분포(Uniform Distribution)

참고. 확률분포간 관계도