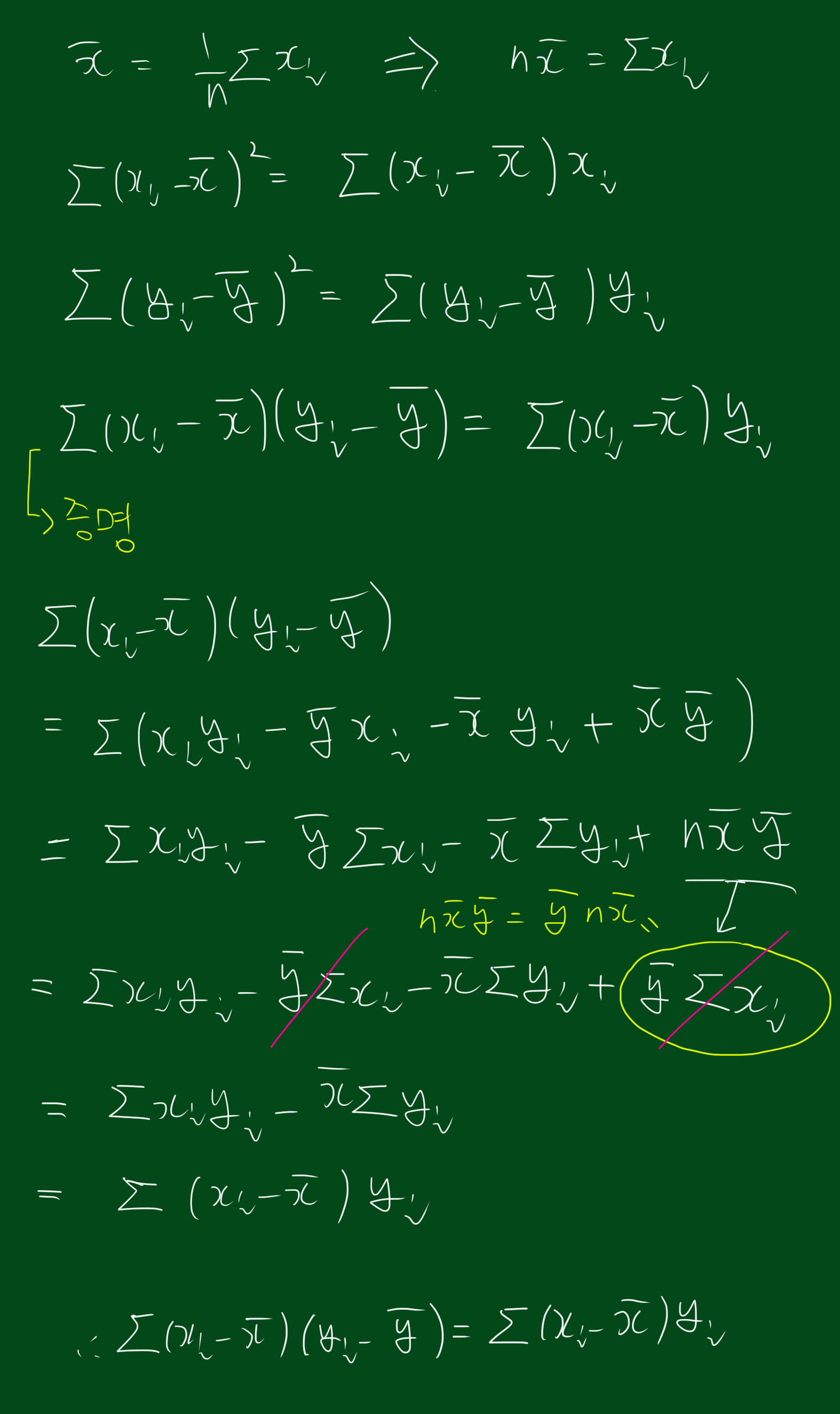[기초통계] 회귀분석의 개념과 의미
업데이트:
회귀분석 정리
참고링크
1. 회귀분석 정의
회귀분석(regression analysis)는 변수들간의 함수관계를 추구하는 통계적 방법이다.
회귀분석은 독립변수와 종속변수 간의 함수관계를 규명하는 통계적 방법입니다. 그렇다면 독립변수와 종속변수는 무엇일까요?
독립변수(independent variable)는 입력값이나 원인을 나타내며, 종속변수(dependent variable)은 결과물이나 효과를 나타낸다.
독립변수는 설명변수(explanatory variable)이라고도 하며, 종속변수는 반응변수(response variable)이라고도 합니다. 독립변수와 종속변수는 $(x_i, y_i)$ 쌍으로 표현하고 독립변수의 집합을 대문자 $X$, 종속변수의 집합을 대문자 $Y$로 표현합니다. 결국 회귀분석이란 독립변수 $X$의 분포를 분석한 후, 종속변수 $Y$의 값을 예측하는 것입니다. 다른 말로하면 다양하게 분포된 $X$가 존재할 때, $Y$의 분포를 알아내는 것입니다.
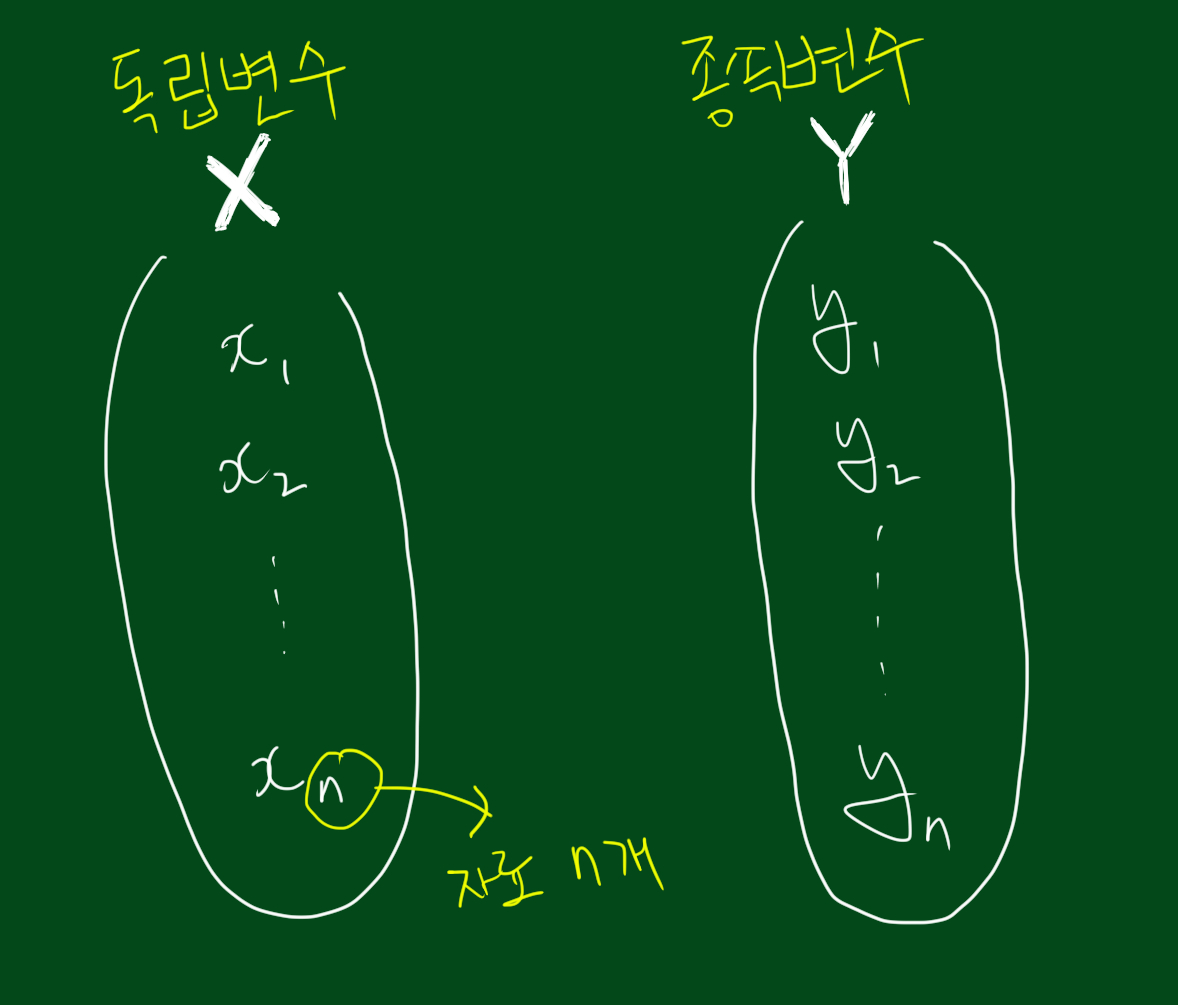
오늘 알아볼 것은 독립변수가 한 개일 경우, 즉 단순회귀분석 부터 알아보겠습니다.
2. 단순회귀분석
2-1. 평균 함수(mean function)
우리가 $Y$의 분포에 대해 관심있을 때 중요한 것이 mean function 입니다.
$ E(Y|X=x) = \text{a function that depends on the value of } x $
데이터에 대해서 생각해보면 데이터는 이미 ‘주어졌다’는 것을 알 수 있습니다. ‘주어졌다’를 다른 말로 바꾸면 ‘정해졌다’라고 할 수 있는데요. 위 식에서 기대값은 $x$값이 ‘이미 정해을때’라는 조건부 기대값으로 볼 수 있습니다. 이를 수식으로 나타내면,
$ E(Y|X=x) = \beta_{0} + \beta_{1}x $
위 mean function을 자세히 살펴보면, 직선이라는 것을 알 수 있는데요. $\beta_{0}$가 절편(intercept)이 되고, $\beta_{1}$은 기울기(slope)입니다. 또한 위 식에서 $\beta_{0} \, \beta_{1}$는 모수이며, 우리가 추정해야할 값입니다.
2-2. 분산함수(variance function)
회귀분석에서 종종 적합 모델에 사용되는 가정은 모든 $x$값에 대해 분산이 동일하다는 것입니다. $x$값이 얼마이든 분산에는 영향을 주지 않고, 분산은 항상 같다는 뜻입니다. 이를 식으로 나타내면 아래와 같습니다.
$ Var(Y|X=x) = \sigma^{2} $
이며, 분산이 얼마인지는 모르는상태(unknown)입니다.
2-3. 통계적 오차(statistical error)
회귀분석에서 빼놓을 수 없는 요소가 바로 오차(error)인데요. 여기서 말하는 에러는 통계적 오차(statistical error)입니다. 왜냐하면 우리가 예상한 종속변수 $y$값은 실제로 관측된 $y$값과 차이가 날 수 있기 때문입니다. 즉, $E(Y|X=x_i)$와 $y_{i}$가 다를 수 있다는 뜻이죠. 이를 수식으로 나타내면 다음과 같습니다.
$ y_{i} = E(Y|X=x_{i})+e_{i} $
$ e_{i} = y_{i} - E(Y|X=x_{i}) = y_{i} - \beta_{0} + \beta_{1}x_i $
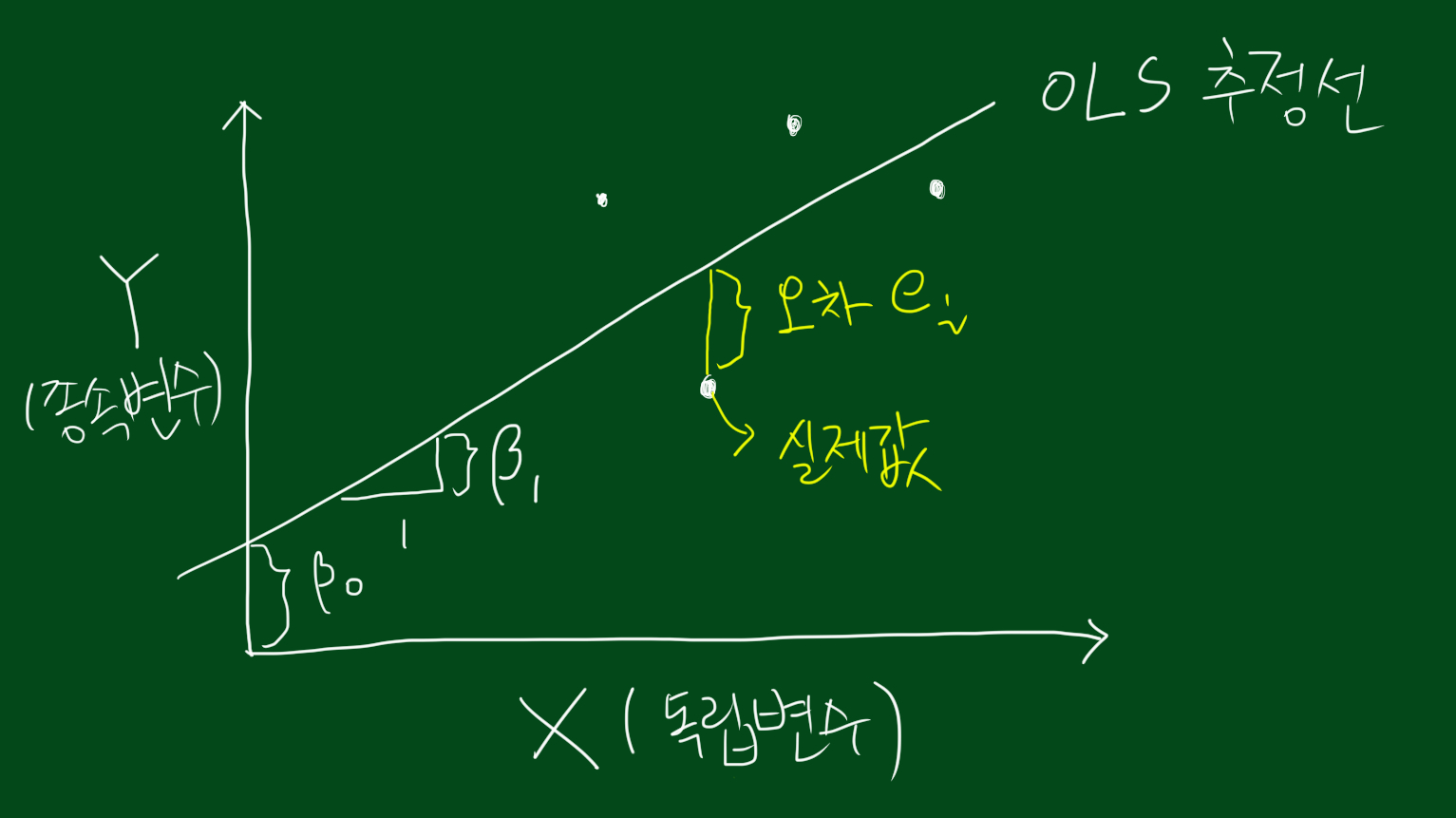
오차항에는 두가지 가정이 필요합니다.
-
오차항의 기대값은 0이다. $E(e|x_{i}) = 0$. 즉, 가로축을 $x_{i}$라고 놓고, 세로축을 $e_{i}$로 놓고 그래프르를 그리면 패턴이 없다는 뜻입니다.
-
오차항은 모두 서로독립(independent)이다. 즉, 하나의 오차는 다른 오차에 대해 어떠한 정보도 줄 수 없다는 뜻 입니다. 영향을 끼치지 않는다는 뜻이죠.
이 밖에도 오차항이 정규분포를 따라야한다는 가정도 있는데요. 이 가정은 다소 강한 가정으로 오차항이 반드시 정규분포를 따라야하는 것은 아닙니다. 또한 오차항은 확률변수이지만 모수는 아닙니다.
참고. 오차 vs 잔차
오차(error)와 잔차(residual)은 비슷한 뜻 이지만 차이가 있습니다. 오차는 모집단을 대상으로 한 회귀식에 쓰는 말이며, 잔차는 표본을 대상으로 쓰는 말입니다.
2-4. 최소제곱법
$ y = \beta_{0} + \beta_{1}x $
위와 같은 회귀분석 식에서 우리가 추정해야할 모수는 $\beta_{0} , \beta_{1}$입니다. 최소제곱법은 바로 이 두가지 모수를 추정하는 방식으로써 오차항의 제곱합을 최소화 하는 방식으로 값을 구합니다.
최소제곱법(ordinary least squares, OLS)은 오차의 제곱합이 최소가 되는 해를 구하는 방법이다.
잠시 표기법에 대해 언급하겠습니다. $y_i$는 실제값을 의미하구요, $\hat{y_i}$는 $i$번째 $y$의 추정치를 의미합니다. 따라서 최소제곱법을 통해 구한 회귀식은 아래와 같이 표현됩니다.
$ \hat{y_i} = \hat{E}(Y|X=x_i) = \hat{\beta_{0}} + \hat{\beta_{1}}x_i $
다음으로 오차항의 추정치는 아래와 같이 나타납니다.
$ \hat{e_i} = y_i - \hat{E}(Y|X=x=x_i) = y_i - \hat{y_i} = y_i - (\hat{\beta_0} + \hat{\beta_1}x_i) $
결국, 최소제곱법이란
$ RSS = \sum_{i=1}^{n}[y_i - (\hat{\beta_0} + \hat{\beta_1}x_i)]^{2} $
을 최소화 시키는 것을 의미합니다. 이 때 RSS를 Residual sum of squares라고 합니다. 최소제곱법을 이용한 모수의 추정치는 아래와 같습니다.
2-5. 최소제곱법으로 구한 모수 추정치
$ \hat{\beta_{1}} = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n}(x_i - \bar{x})^{2} } $
$ \hat{\beta_{0}} = \bar{y} - \hat{\beta_{1}} - \hat{\beta_{1}}\bar{x} $
2-6. 분산 추정
$ \hat{\sigma^2} = \frac{RSS}{n-2} $
2-7. 모형 설명력
우리가 만든 회귀모형이 얼마나 설명력이 있을까요? 모형의 설명력은 변동성 개념을 이용해서 표현합니다. 전체 변동성은 크게 설명가능한 변동성과 설명 불가능한 변동성으로 나뉩니다. 전자는 모형내부의 변동성이며, 후자는 오차의 변동성입니다. 오차의 변동성의 경우 말그대로 오차에 의한 것이므로 설명할 수 가 없습니다. 즉, 오차의 변동성이 작을수록 모형설명력은 높아집니다. 이를 흔히 R제곱값이라고 부릅니다.
$ \textbf{R^2} = \frac{SSreg}{SYY} = 1 - \frac{RSS}{SYY}$
$ \textbf{R^2} = \frac{\text{모형 변동성}}{\text{전체 변동성}} = \frac{SSreg}{SYY} = \frac{(SXY)^2}{SXX \times SYY} = r_{xy}^{2} $
R제곱값은 0과 1사이의 값을 가지며 1에 가까울수록 설명력이 높다는 것을 의미합니다. 위 식에서 SXX는 x의 제곱합을 의미하고, SYY는 y의 제곱합, $r_{xy}$는 표본 상관계수를 의미합니다. R제곱값에는 한가지 단점이 있는데요. 변수를 많이 추가할수록 R제곱값이 높아진다는 것입니다. 따라서 분석가는 무작정 변수를 추가함으로써 모형설명력이 높다고 착각할 수 있는데요. 이를 보완하기 위해 나온 것이 adjusted R제곱값 입니다.
$ \textbf{R}_{adj}^{2} = 1 - \frac{RSS/df}{SYY/(n-1)}$
얼핏 보기에는 R제곱값과 비슷하지만 adjsted R제곱값은 자유도를 고려합니다. 따라서 변수를 무작정 추가했을때 설명력이 높아지는 것을 막을 수 있습니다.
2-8. 모형 진단
모형을 구한 후에는 모형이 적합한지 검증이 필요합니다. 앞서 모형 설정 이전에 여러가지 가정을 했었는데요. 모형 진단에서는 해당 가정들을 만족하는지 보는 것입니다. 흔히 하는 것은 아래 그림 처럼 ‘잔차(residual) vs 적합값(fitted values)’플랏을 그려 보는 것입니다.
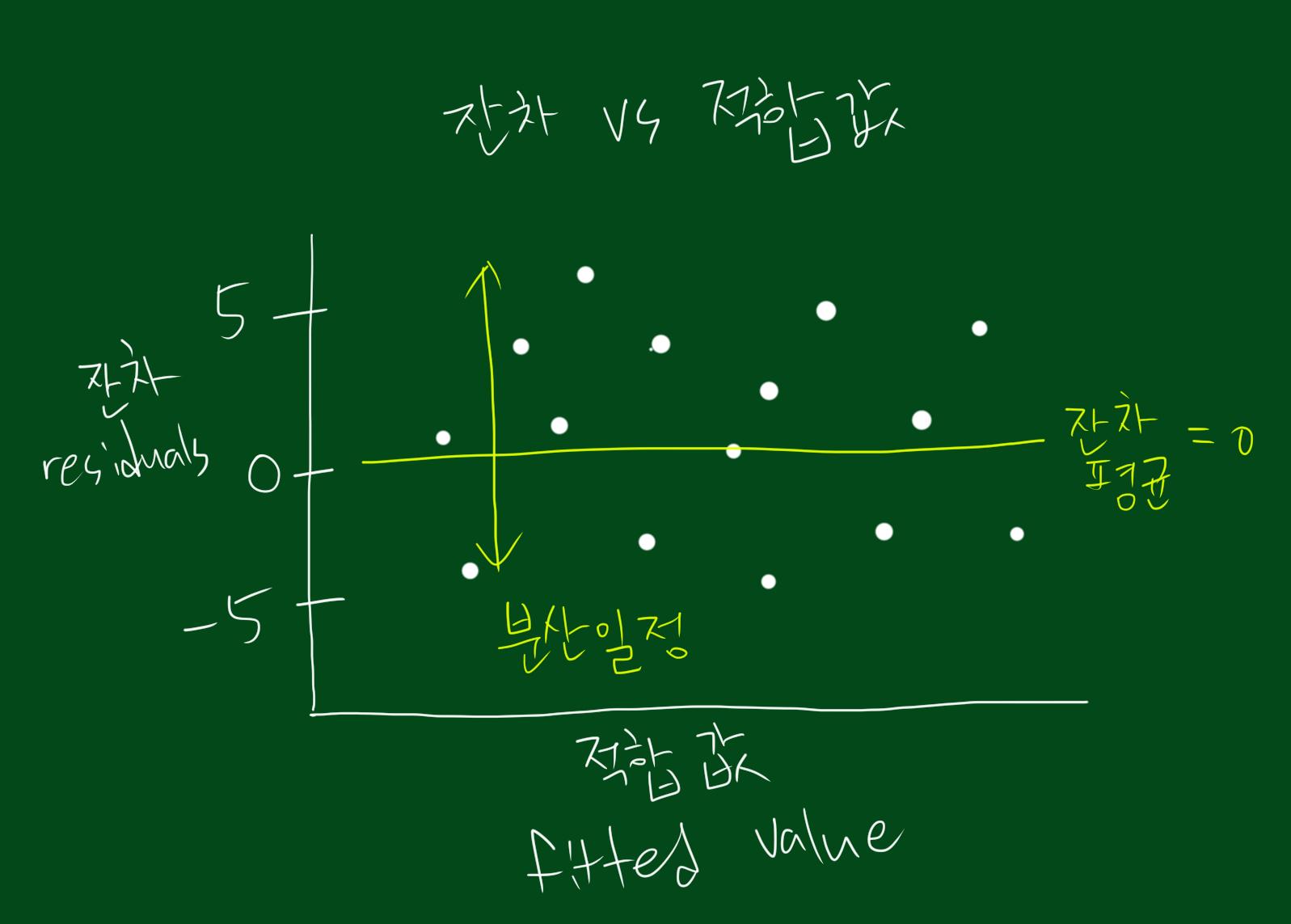
위 그림에서 봐야할 것은 잔차의 평균이 0인지, 분산이 일정한지 입니다. 위 그림은 두 조건 모두 만족하네요. 따라서 위와 같은 플랏 형태가 나타난다면 회귀모형이 적합하다는 것을 알 수 있습니다.
3. 다중회귀분석(multiple regression)
다중회귀분석은 단순회귀분석과 다르게 독립변수가 한 개가 아닌 여러 개 인 경우를 뜻합니다. 식으로 나타내면 아래와 같은데요.
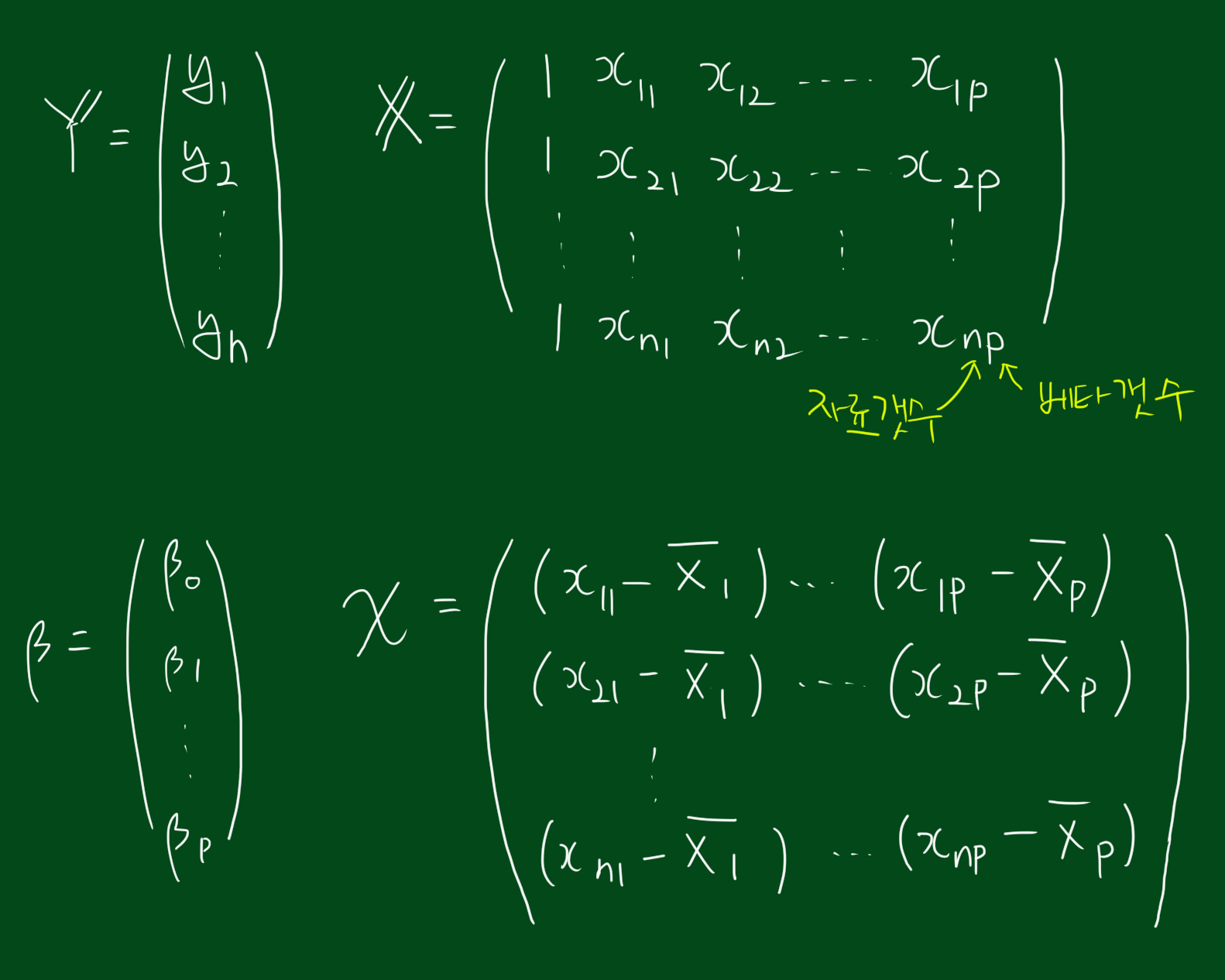
$ E(Y|X) = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + \dots + \beta_{p}x_{p} $
3-1. 평균 함수(mean function)
다중회귀의 평균 함수는 다음과 같습니다.
$ E(\mathbf{Y}|\mathbf{X}) = \mathbf{X}\mathbf{\beta} $
이 때, $X$는 $n \times (p+1)$ 행렬입니다.
3-2. 오차항 e
기본적으로 단순회귀분석 때와 같은 개념입니다. 다만 행렬로 표현했을 뿐 입니다.
$ E(\mathbf{e}|X)=0 , \,\,\, Var(\mathbf{}|X) = \sigma^{2}\mathbf{I_n} $
$ (\mathbf{e}|X) \sim N(0, \sigma^{2}\mathbf{I_n}) $
3-3. OLS 추정
OLS 추정 또한 단순회귀때와 같습니다. 단지 행렬로 표현했을 뿐인데요. 물론 단순회귀때도 아래와 같이 행렬로 계산해도 같은 결과가 나옵니다.
$ RSS(\beta) = \sum(y_i - \mathbf{x_{i}^{T}})^{2} = (\mathbf{Y}-\mathbf{Y}\mathbf{\beta})^{T}(\mathbf{Y}-\mathbf{Y}\mathbf{\beta}) $
$ \hat{\beta} = (\mathbf{X^{T}}\mathbf{X})^{-1}\mathbf{X^{T}}\mathbf{Y} $
부록