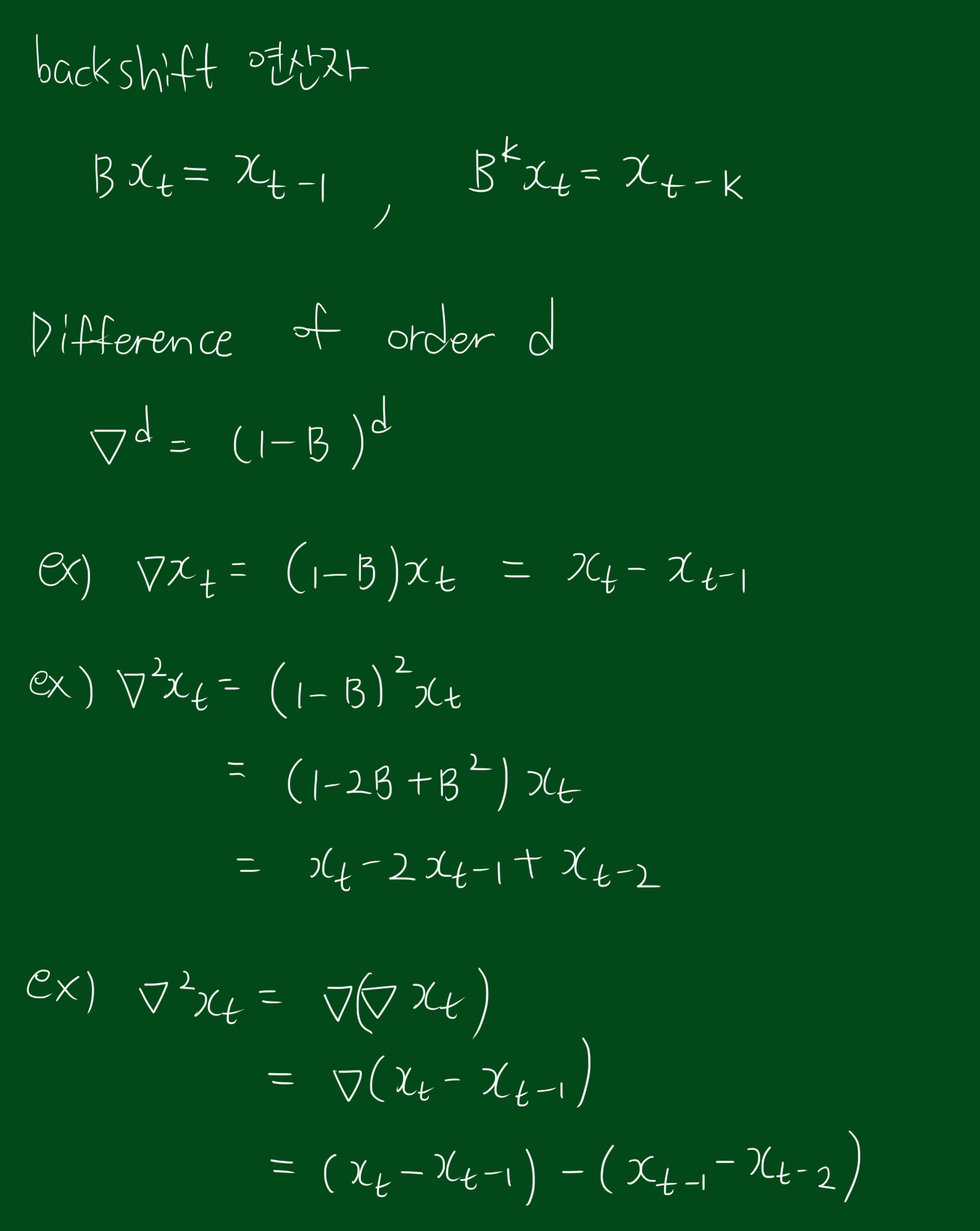[기초통계] 시계열분석(1) AR, MA의 기초
업데이트:
시계열분석의 개념과 의미
참고링크
시계열분석의 필요성
전통적인 통계적 모델링에서 흔히 하는 가정이 있습니다.. 바로 iid인데요. 한글로하면 독립항등분포라는 개념인데, 사실 이 가정은 굉장히 강한 가정입니다. iid를 만족하려면, 서로 다른 관측값들이 서로 독립이고 동일한 분포를 따라야하는데, 이 성질을 만족시키키 쉽지 않습니다. 실제 데이터에서 관측값들은 서로 상관관계가 있는 경우가 대부분이죠. 이런 이유로 시계열분석이 필요한 것입니다. 시계열분석은 주로 time correlation이 존재하는 데이터에 많이 사용되는데요. 주로 시간과 엮여있는 데이터에 사용됩니다. 예를 들어, 시간의 흐름에 따른 경제관련 데이터라던지, 시간의 흐름에 따른 전염병 데이터 등에 시계열분석이 쓰입니다.
회귀분석 vs 시계열분석
회귀분석에서 $x_{1}$은 첫번째 데이터를 의미했는데요. 시계열분석에서 $x_{1}$은 첫번째 ‘시점’, 즉 시점 1에서의 데이터를 의미합니다. 회귀분석에서 $x_{1}$과 $x_{2}$는 그저 서로다른 데이터라는 것만을 의미했지만, 시계열분석에서 $x_{1}$과 $x_{2}$는 시점의 차이가 존재합니다. 정리하면 시계열분석에서 특정 변수는 다른 변수들로 설명가능합니다. 이 때 시점은 같은 시점의 데이터들이지요. 반면 시계열분석에서는 특정 변수를 설명하는 것이 해당 변수 자신의 과거 데이터 입니다. 시계열분석에서는 특정변수를 설명하는데 다른
시계열 성분
시계열 성분은 크게 불규칙성분(irregular component)와 체계적성분(systematic component)로 나뉩니다.. 그리고 체계적성분은 다시 추세성분(trend component), 계절성분(seasonal component), 순환성분(cyclical component)로 나뉩니다.
- 추세가 없다는 말은 시계열 자료의 평균이 시간 축에 평행하다는 것을 의미합니다..
백색소음
백색소음(white nosise)은 물리적으로 전도체 내부에 있는 이산적인 전자의 자유 운동으로부터 야기되는 잡음이다.
라고 위키백과에 나와있는데요. 이 백색소음이 시계열분석에서도 쓰입니다. 시계열분석 데이터는 서로 correlated 되어있다고 앞서 말씀드렸는데요. 백색소음은 서로 uncorrelated 되어있는 확률변수로부터 추출한 데이터 입니다. t시점에서의 백색소음은 $w_t$라고 표기하고 평균 0, 분산 $\sigma_{w}^{2}$을 따릅니다.
$ w_t \sim wn(0, \sigma_{w}^{2}) $
여기서 wn은 white noise의 약자입니다. 시계열분석은 이 백색소음(white noise)로부터 시작합니다.
참고: 평균(mean function)
$ \mu_{xt} = E(x_t) = \int_{-\infty}^{\infty} xf_{t}(x) dx $
이동평균법(moving average)
시계열분석의 기본 단계로 유명한 두가지 모델이 있습니다. 하나는 지금 소개시켜드릴 이동평균법(moving average)이구요, 또하나는 자기회귀(autoregression)입니다. 이 두가지 모형이야말로 시계열분석의 알파이자 오메가라고 생각하시면 됩니다. 먼저 이동평균법에 대해 알아봅시다.
이동평균법(moving average)는 전체 데이터 집합의 여러 하위집합에 대한 일련의 평균을 만들어 데이터 요소를 분석하는 계산이다.
즉, 위 이동평균법을 쉽게 말하면 최근 m개의 관측값들만 이용해 평균을 구하고 이를 이용해 예측하는 방법을 의미합니다. 이동평균이라는 말을 보면 이동+평균 이라고 이해할 수 있는데요. 쉽게 말해 평균은 평균인데, 이동하는 평균이다? 여기서 말하는 이동을 설명드리기 위해서 이동평균법 식을 보여드리겠습니다.
$ v_t = \frac{1}{3}(w_{t-1} + w_{t} + w_{t+1})$
위 식이 간단한 이동평균의 예 인데요. 가장 먼저 알 수 있는 것은 이동평균법에 의해 만들어진 변수 $v_t$는 백색소음으로’부터’ 만들어진 파생변수라는 것입니다. 그리고 우변을 보시면 세개의 백색소음에 대한 평균을 구하는 것을 볼 수 있는데요. 이 때 세가지 항에 대해 봅시다. 이 세가지 항은 데이터 전체가 아닙니다. 특정 항에 대해 현재, 미래시점으로 1시점만큼 ‘이동’한 값들의 평균이죠. 예를들어 100 시점이라고 하면 $\frac{1}{3}(w_{99} + w_{100} + w_{101})$이 되겠죠. 이것이 이동평균의 개념입니다. 평균을 구하긴 구하는데 시점을 이동시키면서 평균을 구하는 것이지요. 그리고 위의 정의에 따라 전체 데이터의 평균이 아닌 평균의 부분집합의 평균입니다. 이동평균법의 또하나의 특징은 예측하고자 하는 데이터 자체를 사용하지 않고 백색소음만 사용한다는 것입니다.
자기회귀(autoregression)
자기회귀(autoregression)모형은 출력변수가 이전 값과 선형적으로 의존하도록 지정합니다.
자기회귀라는 말을 들었을 때는 뭔가 회귀분석이랑 비슷할 것 같은 느낌이 듭니다. 하지만 회귀분석과는 다소 차이가 있는데요. 회귀분석에서는 독립변수 $X$로 종속변수 $Y$를 예측합니다. 하지만 자기회귀는 이름에서도 알 수 있듯이 $X$를 이용하는데 $X$자신을 이용합니다. 즉, 특정 시점의 값을 예측하기위해 이전 시점의 값들을 이용하는 것이지요. 이동평균법과의 차이는 이동평균법은 백색소음만 사용하지만, 자기회귀에서는 자기자신의 값과 백색소음을 함께 사용합니다.
$ x_t = x_{t-1} - 0.7x_{t-2} + w_t $
위 식은 간단한 자기회귀모형인데요. 식을 보시면 $t$시점의 $x$값을 예측하기 위해서 1시점, 2시점 과거의 데이터 및 백색소음을 사용하는 것을 보실 수 있습니다. 즉, $x$를 예측하기 위해서는, $x$자신의 2시점 이전까지의 데이터만 있으면 충분하다는 뜻입니다.
자기공분산(autocovariance)
자기공분산을 보시기전에 공분산 포스팅을 먼저 보시면 이해가 쉬우십니다. 자기공분산은 이름그대로 서로다른 변수 $X$, $Y$ 사이의 공분산이 아닌, 같은 $X$변수이지만 $s$시점과 $t$시점간의 공분산입니다. 자기공분산은 아래와 같이 정의 됩니다.
$ \gamma_{x}(s, t) = cov(x_s, x_t) = E[(x_{s} - \mu_{s})(x_{t} - \mu_{t})] $
위 정의를 보시면 일반적인 공분산과 큰 차이가 없다는 것을 알 수 있습니다. 참고로 시점이 같은 변수의 자기공분산은 아래와 같습니다.
$ \gamma_{t}(t, t) = E[(x_{t} - \mu_{t})^{2}] = var(x_{t}) $
참고로 백색소음의 자기공분산은 이렇습니다.
$
\gamma_{x}(s, t) = cov(w_s, w_t) =
\begin{cases}
\sigma_{w}^{2} & \quad s=t
0 & \quad s \neq t
\end{cases}
$
위 식의 의미는 백색소음의 자기공분산은 시차가 다를 때는 0이라는 뜻입니다.
자기상관관계(autocorrelation)
자기상관관계 함수(autocorrelation function, ACF)의 정의는 다음과 같습니다.
$ \rho(s,t) = \frac{\gamma(s,t)}{\sqrt{\gamma(s,s)\gamma(t,t)}} $
상관계수와 마찬가지로 ACF도 -1에서 1사이의 값을 가집니다.
교차공분산(cross-covariance), 교차상관관계(cross-correlation)
지금까지는 $x$변수 하나에 대해서 생각했는데요. 시계열분석도 회귀분석과 마찬가지로 두 가지 변수를 비교할 수도 있습니다. 시계열분석에서 서로다른 두 변수에 대한 공분산, 상관계수를 교차상관관계(cross-correlation)라고 하는데요.
$x_t$, $y_t$의 교차공분산의 정의는 아래와 같습니다.
$ \gamma_{xy}(s,t) = cov(x_s, y_t) = E[(x_{s} - \mu_{xs})(y_{t} - \mu_{yt})] $
교차상관관계의 정의는 아래와 같습니다.
$ \rho_{xy}(s,t) = \frac{\gamma_{xy}(s,t)}{\sqrt{\gamma_{x}(s,s)\gamma_{y}(t,t)}} $
정상성(stationary)
정상성(stationary)이란 시계열의 확률적인 성질들이 시간의 흐림에 따라 불변이라는 것을 의미합니다.
강 정상성(strictly stationary)
$ P(x_{t_1} \leq c_{1}, \dots , x_{t_k} \leq c_{k}) = P(x_{t_{1+h}} \leq c_{1}, \dots x_{t_{k+h}} \leq c_{k}) $
강정상성은 시계열자료의 시점을 특정시점 이후로 옮겼을때의 확률이 같은 것을 의미합니다.
약 정상성(weak stationary)
일반적으로 정상성이라고 하면 약정상성을 의미합니다. 약정상성은 강정상성 보다는 다소 약한데요.
- $m_t$는 상수이며, 시점 $t$에 의존하지 않는다.
- 자기공분산함수 $\gamma(s,t)$는 $s$와 $t$의 차이만큼, 즉, $|s-t|$에만 의존한다.
두번째 조건에 대해 조금 더 설명드리면 아래와 같습니다.
$ \gamma(t+h, t) = cov(x_{t+h}, x_t) = cov(x_h, x_0) = \gamma(h, 0)$
즉 자기공분산 함수에서 h만큼 시간차가 난다고 했을때, h만큼의 간격만 유지하면 자기공분산 함수가 그대로 성립한다는 뜻이죠. 정상성을 만족시킬때의 자기공분산(autocovariance) 함수는 다음과 같습니다.
약정상성을 만족시킬때의 자기공분산함수(autocovariance function)
$ \gamma(h) = cov(x_{t+h}, x_t) = E[(x_{t+h}-\mu)(x_{t}-\mu)] $
약정상성을 만족시킬때의 자기상관함수(autocorrelation function, ACF)
$ \rho(h) = \frac{\rho(t+h, t)}{\sqrt{\rho(t+h, t+h)\rho{t,t}}} = \frac{\rho(h)}{\rho(0)} $
시계열분석을 위한 기본적인 연산자 정리