ROC Curve(ROC 커브)란? 머신러닝 모형 평가

머신러닝 성능 평가 - ROC 커브 개념 정리

참고링크

머신러닝

• k-means클러스터링 복습하기
• k-최근접 이웃 알고리즘 복습하기
• 선형회귀분석 복습하기
• 로지스틱 회귀분석 복습하기
• 릿지, 라쏘 회귀분석 북습하기
• 의사결정나무 복습하기
• 서포트벡터머신 복습하기
• 원클래스 SVM 복습하기
• LDA 복습하기
• 가우시안 혼합 모형(GMM) 복습하기
• 딥러닝 기초 복습하기
• 부스팅(boosting) 복습하기
• 사이킷런 실습하기

딥러닝

• 딥러닝 기초(1) 신경망이란
• 딥러닝 기초(2) 성능함수란
• 딥러닝 기초(3) 편미분을 이용한 신경망 학습
• 딥러닝 기초(4) 교차연결
• 딥러닝 기초(5) 합성곱 신경망

모형평가

• ROC 커브 복습하기
• 교차검증(cross validataion)
• 실루엣 스코어

최적화

• 컨벡스 셋(convex set)
• 컨벡스 함수(convex function)
• 라그랑주 듀얼 함수
• Karush-Kuhn-Tucker

1. ROC 커브란 무엇일까요?

여러분이 머신러닝 모델을 만들었다고 가정합시다. 모델을 만들었으면 이 모델이 성능이 좋은지 안좋은지 평가를 해야 하겠죠? ROC 커브는 머신러닝 모델을 평가할 때 쓰입니다.

2. 민감도와 특이도

ROC 커브를 이야기 하기전에 민감도(Sensitivity)와 특이도(Specificity)의 개념을 아셔야 합니다. 흔히 민감도와 특이도를 설명하기 위해 의사의 진단을 예를 듭니다. 의사는 환자를 진단해 병에 걸렸느냐 안 걸렸느냐를 판단합니다. 이때 발생할 수 있는 경우는

모수	실제론 병에 걸림	실제론 정상인
검사결과 양성	양성판정을 내렸는데 실제로 병에 걸린 경우(TP)(1)	양성판정을 내렸는데 실제로는 정상인(FP)(2)
검사결과 음성	음성판정을 내렸는데 실제로 병에 걸린 경우(FN)(3)	음성판정을 내렸는데 실제로는 정상인(TN)(4)

위의 표를 좀 더 간략히 표현하면

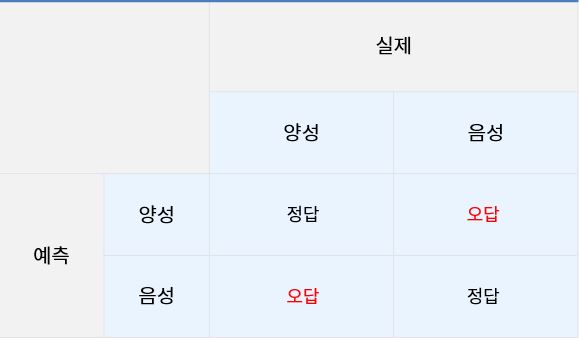
위 그림처럼 크게는 정답과 오답으로 나눌수 있으며 자세히는 아래처럼 나타냅니다.

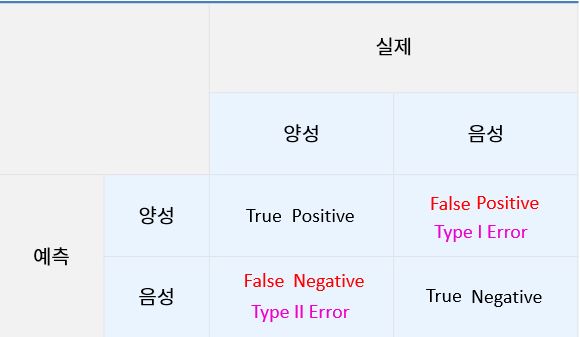
• 민감도(Sensitivity, True positive rate(TPR), Recall): 실제 병에 걸린 사람이 양성(Positive) 판정을 받는 비율입니다.
• 특이도(Specificity, True Negative rate(TNR) ): 정상인이 음성(Negative) 판정을 받는 비율입니다.
• False positive rate(FPR) = 1-specificity
• 정확도(Accuracy): 전체 데이터 중 제대로 분류된 데이터 비율
• 에러율(Error Rate): 전체 데이터 중 제대로 분류되지 않은 데이터 비율
• 정밀도(Precision): Positive로 예측했을 때, 실제로 Positive인 비율

$ \texttt{민감도(Sensitivity, Recall, True Positive Rate)} = \frac{(1)}{(1)+(3)} = \frac{TP}{TP + FN} $

$ \texttt{특이도(Specificity, True Negative rate)} = \frac{(4)}{(2)+(4)} = \frac{TN}{FP + TN}$

$ \texttt{False positive rate(FPR)} = \frac{(2)}{(2)+(4)} = \frac{FP}{FP + TN}$

$ \texttt{정확도(Accuracy)} = \frac{(1)+(4)}{(1)+(2)+(3)+(4)} = \frac{TP + TN}{TP + FP + FN + TN}$

$ \texttt{에러율(Error Rate)} = \frac{(2)+(3)}{(1)+(2)+(3)+(4)} = \frac{FP + FN}{TP + FP + FN + TN} $

$ \texttt{정밀도(Precision)} = \frac{(1)}{(1)+(2)} = \frac{TP}{TP + FP}$

2-1. 정밀도(Precision)와 민감도(Recall)

$ \texttt{정밀도(Precision)} = \frac{TP}{TP + FP}$

$ \texttt{민감도(Recall)} = \frac{TP}{TP + FN} $

Precision과 Recall의 차이는 무엇일까요? 위 식을 보시면 분모는 같습니다. True Positive가 분모의 일부라는 것도 같네요. Precision을 보시면 분모가 TP + FP이므로 Positive 라는 판정을 내렸다는 뜻입니다. 즉, 자신의 ‘양성판정’이 기준이라는 것입니다. 반면 Recall을 보면 분모가 TP + FN 이므로 ‘옳은판정’이 기준입니다. 즉, Precision과 recall은 기준이 다르다는 차이가 있습니다.

3. ROC 커브

결국 모형이 좋다는 말의 뜻을 생각해보면, 모든 환자에게 양성 판정을 내리고, 모든 정상인에게 음성 판정을 내리면 완벽합니다. 만약 모든 진단에 대해 양성 판정을 내리면 어떻게 될까요? 이 경우 병에 걸린 모든 환자를 찾을 수 있습니다. 왜냐면 모든 사람이 양성 판정을 받기 때문이죠. 하지만 정상인도 환자로 판정 받는 다는 단점이 있습니다. 그럼 모든 진단에 대해 음성 판정을 내리면 어떻게 될까요? 이 경우에는 모든 정상인에 대해 올바른 판정이 내려집니다. 하지만 병에 걸린 환자 또한 정상인이라고 판정 받으므로 병을 치료할 수 없습니다.

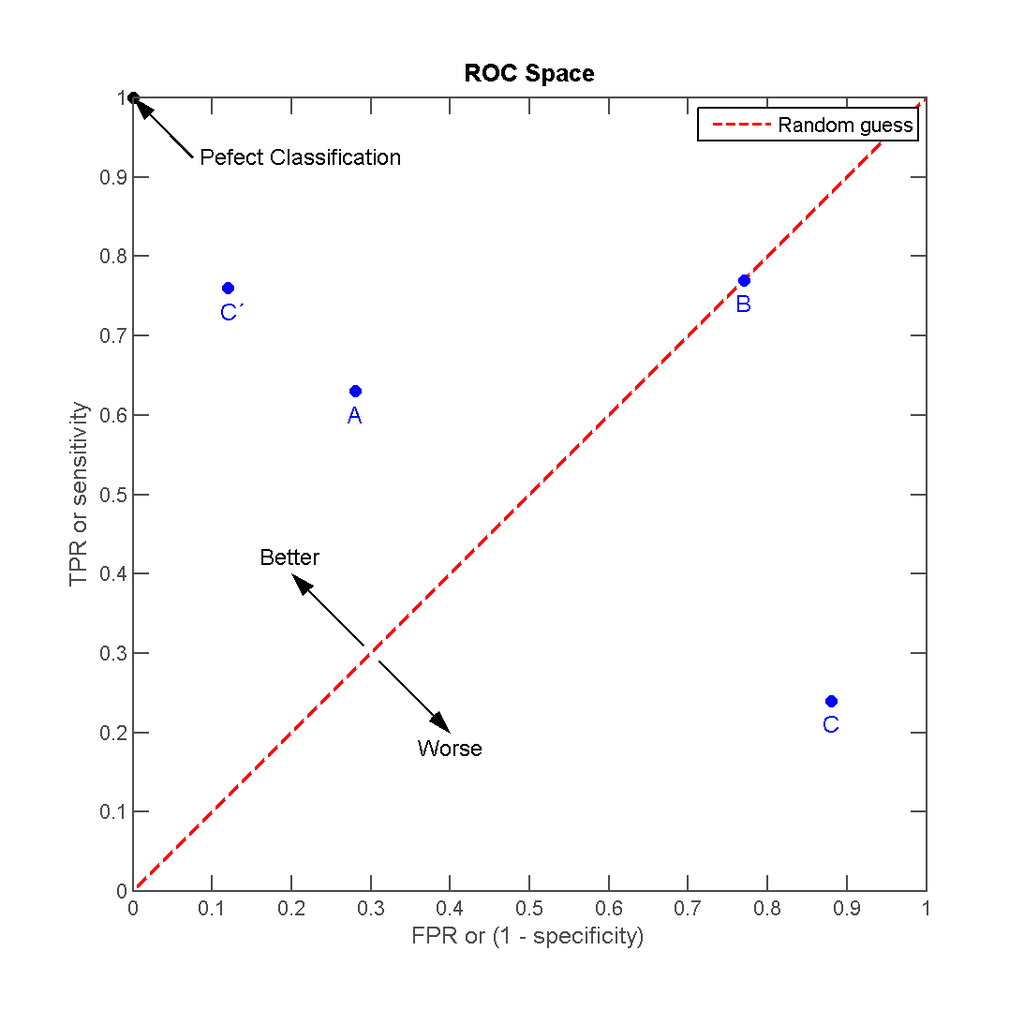
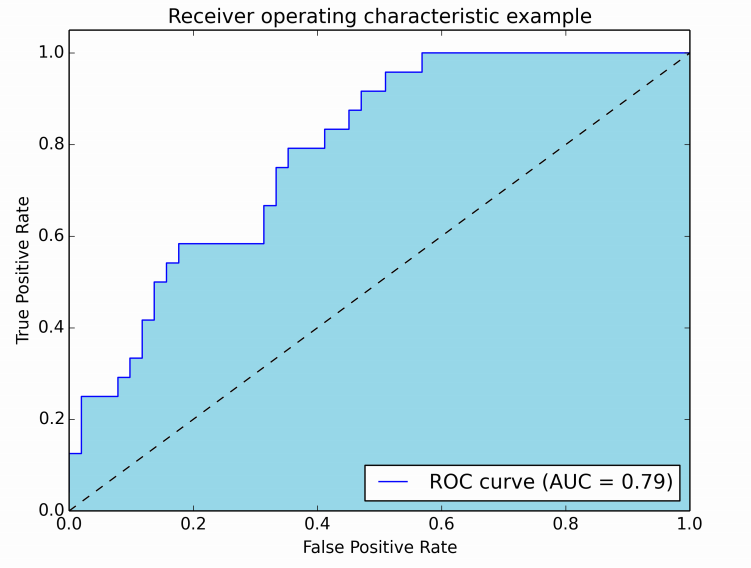
ROC 커브는 이러한 다양한 부분을 한눈에 볼 수 있는 판정법입니다. Figure1에서 보면, 병에 걸린 사람을 양성 판정하고, 정상인을 정상인이라 판정하는 가장 이상적인 판정, 즉, TPR = 1 이고, FPR = 0 인 경우가 가장 이상적입니다.(Perfect Classification)

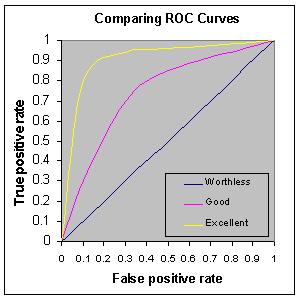
ROC 커브에서 모델의 평가가 좋다는 것은 커브의 밑면적 즉 AUC의 넓이가 넓을 수록 그 모델의 성능이 좋다는 것.