[머신러닝] 가우시안 혼합 모델(Gaussian mixture model) 기초 개념
업데이트:
가우시안 혼합 모델(Gaussian mixture model) 기초 개념
참고링크
가우시안 혼합 모델 정의
혼합 모델은 통계학에서 전체 집단안의 하위 집단의 존재를 나타내기 위한 확률 모델이다.
즉, 가우시안 혼합 모델은 전체 집단의 하위 집단의 확률분포가 가우시안 분포를 따르는 경우를 말합니다. 흔히 정규분포를 가우시안 분포라고도 부르니 혼동 없으시길 바랍니다. 또한 가우시안 혼합 모델은 비지도학습의 한 종류로, 데이터 클러스터링(clustering)에 사용합니다.
가우시안 혼합 모델 예시
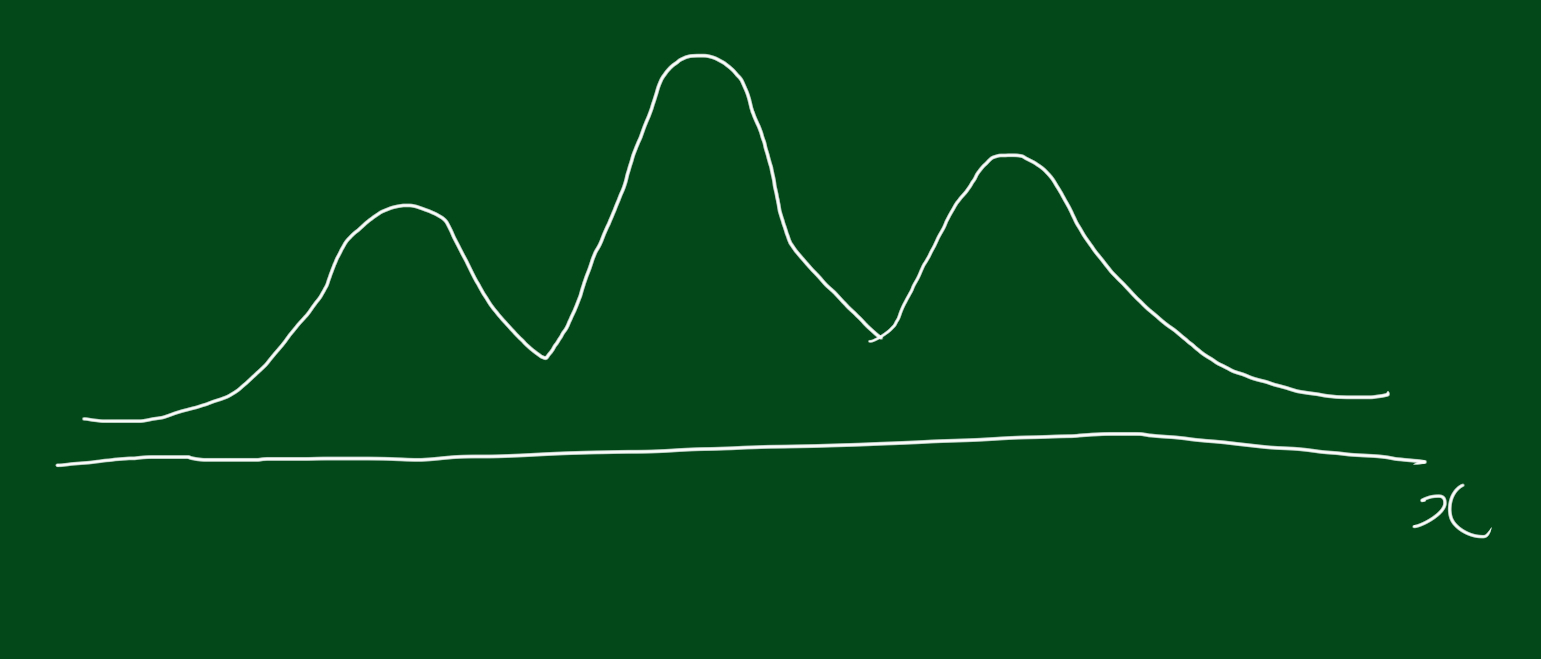
확률분포가 위와 같다고 합시다. 위 분포를 하나의 덩어리라고 생각할 수도 있지만, 아래와 같이 세 가지 가우시안 분포의 결합된 형태라고 생각할 수도 있습니다.
우리가 추정해야할 모수
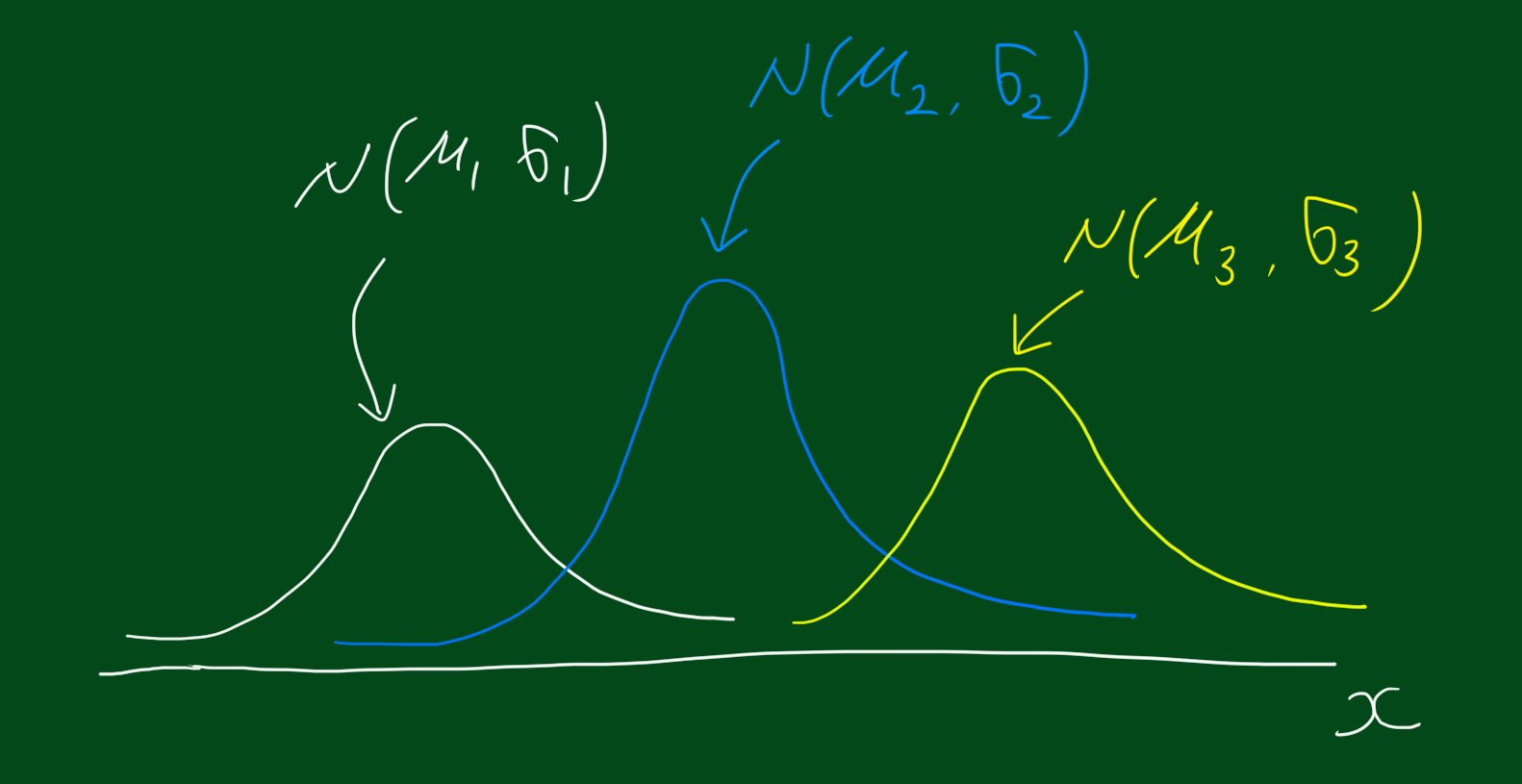
위 그림처럼 전체 집단의 하위 집단이 가우시안 분포 3개라고 가정합니다. 이 경우, 저희가 추정해야 할 모수는 총 9개 입니다. 하나하나 살펴보죠. 먼저 분포가 가우시안 분포를 따르는 하위집단 1개만 살펴봅시다. 가우시안 분포의 경우, 모수는 평균($\mu)$, 분산($\sigma$)입니다. 여기서 하나를 더 추정해야하는데요, 그것은 전체분포에 대한 해당 하위분포의 비율입니다. 이를 $\pi$라고 하겠습니다, 다른 말로하면 해당 데이터가 해당 하위집단에 속할 확률입니다. 그럼 정리해서 첫번째 하위집단의 모수는 $(\mu_1, \sigma_1, \pi_1)$ 입니다. 그럼 자연스럽게 하위집단이 3개이므로, 나머지 두집단의 모수는 $(\mu_2, \sigma_2, \pi_2)$, $(\mu_3, \sigma_3, \pi_3)$가 됩니다.
확률변수 X의 확률밀도함수
그렇다면 위 정보를 토대로 확률변수 X의 확률 밀도 함수를 살펴봅시다.
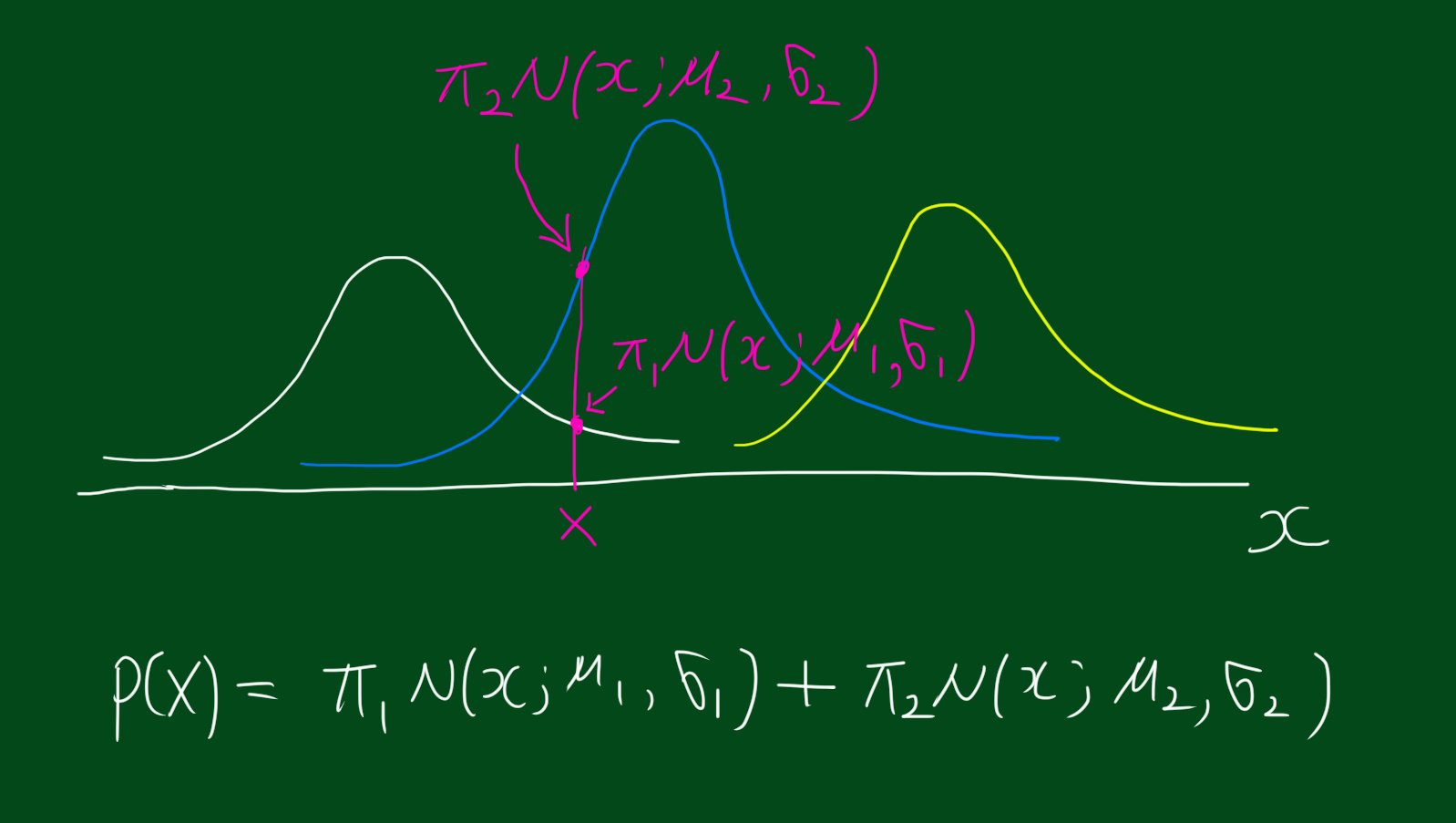
$ p(x) = \sum_{c}\pi_c N(x; \mu_c, \sigma_c)$
위 식에서 $c$는 $c$번째 집단을 의미합니다. $c=1,2,3$. 또한 N은 가우시안 분포라는 뜻이구요, $N(x; \mu_c, \sigma_c)$는 평균이 $\mu_c$, 분산이 $\sigma_c$인 가우시안 분포에서 추출한 데이터라는 뜻입니다. 이를 좀더 풀어쓰면 아래와 같은데요. 아래 식은 참고만 하시고 꼭 외울 필요는 없습니다.
참고: 다변량 가우시안 분포(Multivariate Gaussian models)
$ N(x; \mu, \Sigma) = \frac{1}{(2\pi)^{d/2}}|\Sigma|^{-1/2}exp{-\frac{1}{2}(x-\mu)^{T}\Sigma^{-1}(x-\mu)} $
그리고 위 분포의 MLE(Maximum Likelihood Estimates)는 다음과 같습니다.
$ \hat{\mu} = \frac{1}{m}\sum_{i}x_i $
$ \hat{\Sigma} = \frac{1}{m}\sum(x_i - \hat{\mu})^{T}(x_i - \hat{\mu}) $
위 식의 m은 전체 데이터 갯수 입니다.
잠재변수(latent variable) z 등장
사실 우리가 고려해야하는 확률변수는 하나 더 있습니다. 이것은 데이터가 집단 c에 속하는 경우, 즉 $z$인데요. 수식으로는 아래와 같이 표현합니다.
$ p(z=c)=\pi_c $
위 식은 z가 c일 확률이 $\pi_c$라는 뜻입니다. 이때, 확률변수 z를 관찰할수 없다고 하여(unobservable) 잠재변수(latent variable)이라고 합니다. 잠재변수에 대해 한가지 더 알수있는 조건부확률이 있습니다. 이는 다음과 같은데요.
| $ p(x | z=c) = N(x; \mu_c, \sigma_c) $ |
위 식의 의미는 간단합니다. 하위집단이 c일때 확률변수 x는 평균이 $\mu_c$, 분산이 $\sigma_c$인 가우시안 분포를 따른다는 것입니다. 정리하면, 우리가 알고있는 식은 두가지입니다.
$ p(z=c)=\pi_c $
| $ p(x | z=c) = N(x; \mu_c, \sigma_c) $ |
EM 알고리즘(Expection Maximization Algorithm)
이제 모수를 추정할 것인데요, 전체 과정은 아래와 같이 E-step, M-step 두가지로 구성되어있습니다. 이를 EM 알고리즘이라고 하는데요. 아래와 같이 E-step과 M-step을 반복하여 로그가능도함수를 증가시키는 방법을 EM알고리즘이라고 합니다. 그럼 한단계씩 알아봅시다.
E-Step
먼저 $r_{ic}$를 구합니다. 어떻게 구하냐면요.
$ p(z=c)=\pi_c $
| $ p(x | z=c) = N(x; \mu_c, \sigma_c) $ |
위 두가지 조건과 베이즈정리를 이용하면 i번째 데이터가 그룹 c에 속할 확률($r_{ic}$라고 표현)을 구할 수 있습니다.
\[\begin{align} r_{ic} &= p(z=c|x) \\ &= \frac{p(z=c, X=x)}{p(x)} \\ &= \frac{p(x|z=c)p(z=c)}{\sum_{c}\pi_{c}N(x; \mu_c, \sigma_c)} \\ &= \frac{\pi_{c}N(x; \mu_c, \sigma_c)}{\sum_{c}\pi_{c}N(x; \mu_c, \sigma_c)} \end{align}\]당연하게도, $r_{ic}$는 확률이므로 0과 1사이 값을 가지구요, 그 값이 1에 가까울수록 c집단에 속할 확률이 높다는 의미입니다. 위 E-step을 통해 i번째 데이터가 c에 속할 확률, 즉 $r_{ic}$를 구했는데요. 다음으로 M-step으로 넘어갑시다.
M-Step
M-step에서 저희가 할 일은 처음에 구하고 싶었던 모수 9개를 구할 것입니다. 그 전에 위에서 구한 $r_{ic}$를 고정시키고 시작할께요.
먼저 c집단 데이터의 수는 $m_c$로 표현하고 아래와 같이 추정합니다.
$ m_c = \sum_{i}r_{ic} $
또한 전체 집단에 대한 하위집단 c의 비율은 아래와 같이 추정합니다.
$ \frac{m_c}{m} $
그리고 각 하위집단의 평균($\mu_{c}$)과 분산($\sigma_c$)는 아래와 같이 추정합니다.
$ \mu_c = \frac{1}{m_c}\sum_{i}r_{ic}x_i $
$ \Sigma_c = \frac{1}{m_c}\sum r_{ic}(x_i - \mu_c)^{T}(x_i-\mu_c) $
자 이렇게 각 클러스터의 모수를 업데이트 시켰습니다.
반복
그리고나서 해야 할 일은 각 E-step과 M-step을 반복시키는 것 입니다.
위 과정을 반복하는 이유
위 과정을 반복하는 이유는 무엇일까요? 그것은 각 스텝이 log-likelihood를 증가시키기 때문입니다. log-likelihood는 아래와 같습니다.
$ log p(x) = \sum log[\sum_{c}\pi_{c}N(x_i; \mu_c, \pi_c)] $
위 과정, E-step과 M-step을 반복함에따라 로그 가능도함수가 특정값으로 수렴하는 것이죠.
EM 알고리즘의 장단점
local optimization 문제가 발생할 수 있습니다. 그리고 k-means clustering과 마찬가지로 초기에 그룹 갯수를 정해줘야하는 단점이 있습니다.


