[머신러닝] LDA(Linear Discriminant Analysis) 선형판별분석의 개념
업데이트:
LDA(Linear Discriminant Analysis), QDA(Quadratic discriminant Analysis)의 개념
참고링크
1. LDA(Linear Discriminant Analysis)의 개념
LDA(Linear Discriminant Analysis)는 이름에서도 알 수 있듯, 선형판별분석, 즉, 선형으로 데이터를 분할 하는 방법이라고 할 수 있겠습니다. 선형으로 분할한다했으니까 직선을 이용해 데이터를 분할 한다고 생각할 수 있습니다. 또한 LDA는 라벨링이 되어있는 지도학습에 속하는 방법입니다. LDA는 기본적으로 베이즈 정리를 이용해 선형판별함수를 구하는데요.
$P(G|X)$ : 클래스 사후확률(posterios)
$ f_k(x) $: 클래스 G=k일 때의 확률변수 X의 조건 확률 밀도 함수(class density)
$ \pi_k $: 클래스 k의 사전확률(prior probability)
위 식을 이용해 베이즈 정리를 이용해 클래스 사후확률 $P(G|X)$을 구하면 다음과 같습니다.
\[\begin{align} P(G=k|X=x) &= \frac{P(G=k, X=x)}{P(X=x)} \\ &= \frac{P(X=x|G=k)P(X=x)}{P(X=x)} \\ &= \frac{f_k(x)\pi_k}{\sum_{l=1}^{K}f_l(x)\pi_l} \\ \end{align}\]클래스 확률 밀도 함수 $f_k(x)$가 아래와 같은 다변량 정규분포(Multivariate normal distribution)를 따른다고 합시다.
$ f_k(x) = \frac{1}{(2\pi)^{p/2}|\Sigma_k|^{1/2}}e^{-\frac{1}{2}(x-\mu_k)^{T}\Sigma_{k}^{-1}(x-\mu_k)} $
LDA에서는 모든 클래스 별 확률밀도함수가 모두 같은 공분산을 가지고 있다고 가정합니다.
$ \Sigma_k = \Sigma $
서로다른 클래스 $k, l$를 비교하기위해 log-ratio를 보겠습니다.
\[\begin{align} log\frac{P(G=k|X=x)}{P(G=l|X=x)} &= log\frac{f_k(x)}{f_l(x)} + log\frac{\pi_k}{\pi_l} \\ &= log\frac{\pi_k}{\pi_l} -\frac{1}{2}(\mu_k + \mu_l)^{T}\Sigma^{-1}(\mu_k-\mu_l) + x^{T}\Sigma^{-1}(\mu_k-\mu_l) \end{align}\]위 식을 좀 더 풀어쓰면 다음과 같습니다.

위 식에서 최종 형태를 보시면 $x$에 대한 선형방정식이라는 것을 알 수 있습니다. 저희는 위에서 클래스별 공분산 행렬이 같다고 가정했으므로 약분되는부분이 많아 계산하기는 좀더 쉬워졌네요. 위의 로그-오즈(log-odds) 함수가 의미하는 것은 클래스 $k$ 집단과 클래스 $l$ 집단의 결정 경계(decision boundary)를 알 수 있다는 것인데요. 즉, $P(G=k|X=x)=P(G=l|X=x)$인 부분은 $x$에 대해 선형이며 $p$차원의 초평면(hyperplane)이라는 것을 알 수 있습니다. 따라서 모든 결정경계는 선형(linear)입니다. 만약 우리가 전체 공간 $\mathbb{R}^p$를 클래스별 영역으로 나눈다면, 각 클래스 영역은 초평면에의해 분할 됩니다. 이 때 중요한 것은 결정경계는 중심에 연결된 선분의 수직 이등분선이 아니라는 것입니다. 결정경계가 중심에 연결된 선분의 수직이등분선이 되려면 공분산 행렬이 $\Sigma = \sigma^2 \mathsf{I}$이어야 하고, 클래스 사전분포 $\pi_k$가 같아야 합니다.
다시 한번 클래스 $k$에 대한 선형판별함수(linear discriminant function)을 봅시다.
$ \delta_k(x) = x^{T}\Sigma^{-1}\mu_k - \frac{1}{2}\mu_{k}^{T}\Sigma^{-1}\mu_k + log\pi_k $
즉, 데이터 $x$가 어떤 클래스에 속하는 지는 $G(x) = argmax_{k}\delta_k(x)$를 구하면 알 수 있습니다.
위에서 각 데이터는 다변량 정규분포를 따른다고 했습니다. 하지만 저희는 아직 모수를 모르기떄문에 아래와 같이 모수 추정을 하겠습니다.
$ \hat{\pi}_{k} = \frac{N_k}{N} $
$ \hat{\mu}k = \sum{g_i = k}\frac{x_i}{N_k} $
$ \hat{\Sigma} = \sum_{k=1}^{K}\sum_{g_i = k}\frac{(x_i - \hat{\mu}_k)(x_i - \hat{\mu}_k)^{T}}{(N - K)}$
예를 들어 두개의 클래스1, 2가 있다고 하고 LDA에 의해 어떤 데이터가 클래스2에 속하려면 아래와 같은 조건을 만족해야합니다.
$ x^{T}\hat{\Sigma}^{-1}(\hat{\mu}_2 - \hat{\mu}_1) - \frac{1}{2}(\hat{\mu}_2 + \hat{\mu}_1)^{T}\hat{\Sigma}^{-1}(\hat{\mu}_2 - \hat{\mu}_1) + log\frac{N_2}{N_1}> 0 $
위 식을 조금 바꾸면 아래와 같습니다.
$ x^{T}\hat{\Sigma}^{-1}(\hat{\mu}_2 - \hat{\mu}_1) > \frac{1}{2}(\hat{\mu}_2 + \hat{\mu}_1)^{T}\hat{\Sigma}^{-1}(\hat{\mu}_2 - \hat{\mu}_1) - log\frac{N_2}{N_1}$
위에서 데이터가 다변량 정규분포를 따른다고 가정했지만, 꼭 다변량 정규분포여야지만 LDA를 쓸 수 있는 것은 아닙니다.
2. QDA(Quadratic discriminant Analysis)의 개념
앞선 LDA에서는 클래스 집단 별 공분산 행렬 $\Sigma_k$가 모두 동일하다고 했습니다. 이걸 조금 더 일반화시켜서 클래스 집단 별 공분산 행렬이 같다는 가정이 없다고 하겠습니다. 그러면 클래스별 로그-비율에서 약분되는 부분이 없어지고 이차판별함수(quadratic discriminant function)은 아래와 같게 됩니다.
$ \delta_{k}(x) = -\frac{1}{2}log\vert \Sigma_k \vert - \frac{1}{2}(x-\mu_k)^{T}\Sigma_{k}^{-1}(x-\mu_k) + log(\pi_k) $
위 판별식에서 볼 수 있듯 클래스 $k$와 클래스 $l$의 결정경계(decision boundary)는 $\delta_{k}(x)=\delta_{l}(x)$이고, 이차식(quadratic equation)을 따릅니다. 위에서 LDA에서는 판별함수가 선형(linear)이었던 것에 반대로, QDA에서는 이차식을 따르네요.
2.1 LDA 결정 경계는 항상 직선?
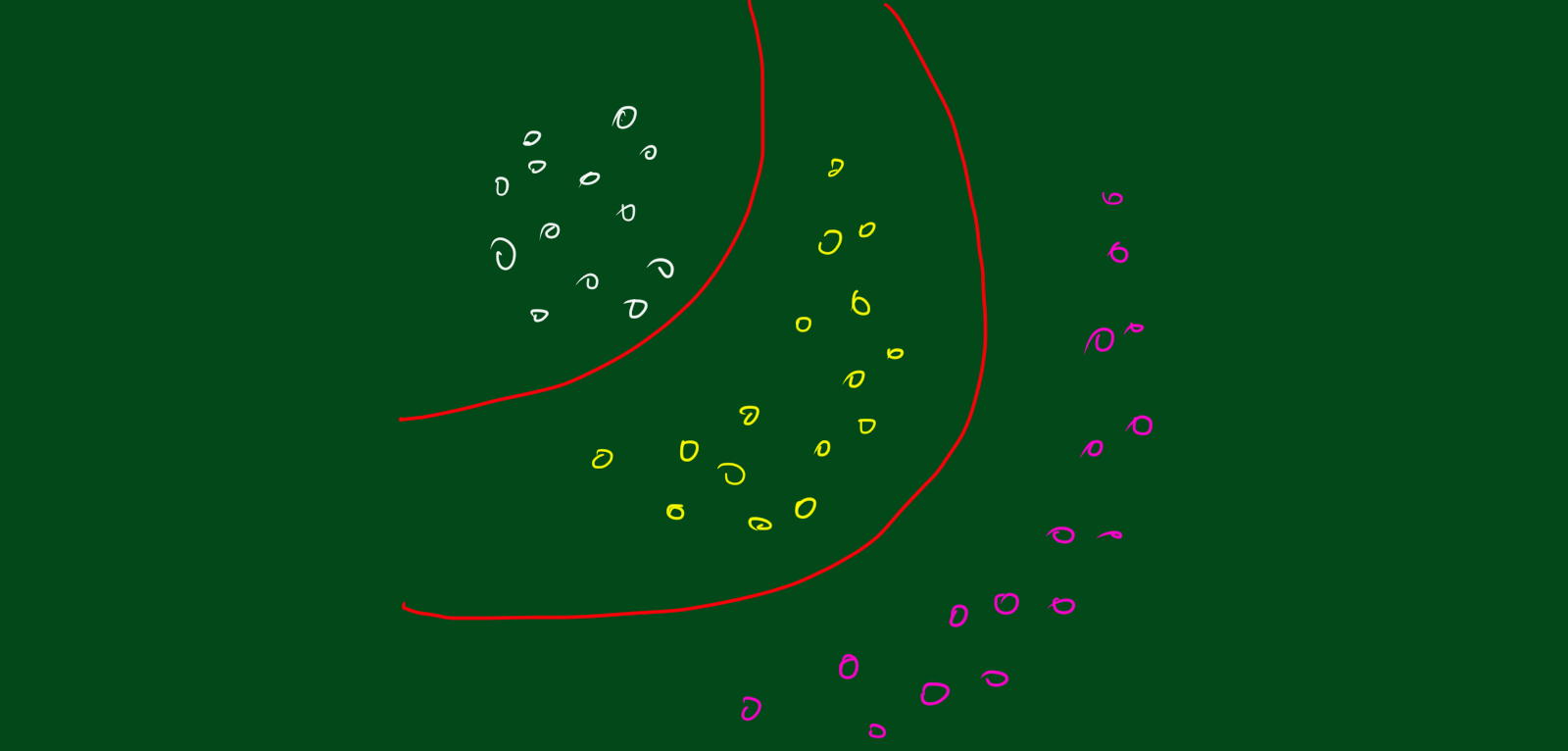
LDA의 판별함수는 선형을 따르니까 LDA를 이용하면 항상 직선만 그려질까요? 그렇지 않습니다. LDA를 이용해서도 곡선의 형태로 판별식을 그릴 수 있는데요. 방법은 바로 데이터 $x$의 공간을 좀 더 높은 차원으로 선형변환 한 후, 확장된 공간에서 LDA를 하는 거죠. 무슨 말이냐면 예를들어 데이터 $x$가 이차원이라고 해봅시다. 그러면 $x = (x_1, x_2)$라고 할 수 있는데, 이 2차원 데이터를 5차원으로 확장시켜봅시다. 예를들어, $x^{*} = (x_1, x_2, x_1 x_2, x_{1}^{2},x_{2}^{2})$로 확장시킨 후 확장된 공간에서 LDA를 하는 거죠. 그러면 결정경계가 곡선의 형태로 나타납니다.
2.2 QDA vs LDA 모수 추정 개수
우리가 사용하는 결정경계는 결국 데이터의 확률밀도함수의 모수에 대한 함수이므로, 우리가 추정해야하는 모수 개수를 구하면 우리가 계산해야할 양을 어느정도 알 수 있습니다. LDA의 경우, $(K-1)\times(p+1)$개의 모수를 추정해야합니다. QDA의 경우에는 $(K-1)\times(p(p+3)/2 + 1)$개의 모수를 추정해야합니다.
2.3 LDA, QDA가 성능 좋은 이유
LDA나 QDA가 좋은 성능을 보이는 이유는 정규분포를 가정했을 때의 모수 추정치가 안정적(stable)이기 때문입니다. 여기서 안정적이라는 말은 bias-variance tradeoff를 의미하는데요, LDA나 QDA를 사용하면 다른 방법에 비해 어느정도 bias는 감수해야하는데, 이유는 bias가 어느정도 있는 대신 분산이 작기 때문입니다.
3. RDA(Regularized Discriminant Analysis)
이번에는 LDA와 QDA를 합친 형태인 RDA(Regularized Discriminant Analysis)에 대해 알아보겠습니다. LDA와 QDA의 차이점은 클래스별 공분산행렬을 같다고 가정하느냐, 아니냐의 차이였습니다. 그렇다면 두 방법을 합치면 클래스별 공분산행렬이 같을 수도 있고, 다를 수도 있다는 것이겠네요. 이를 수식으로 나타내면 아래와 같습니다.
$ \hat{\Sigma}_k(\alpha) = \alpha\hat{\Sigma}_k + (1-\alpha)\hat{\Sigma} $
위 식에서 $\hat{Sigma}$는 LDA에서 쓰이는 공통 공분산 행렬(pooled covariance matrix)입니다. 그리고 위 식에서 알파의 값에 따라 공분산행렬이 달라지는 건데요, 알파값이 0이라면 LDA가 되고, 알파값이 1이라면 QDA가 됩니다. 알파값은 0과 1사이 이며, 크로스밸리데이션을 통해 결정됩니다.
4. LDA 계산
위에서 LDA, QDA의 개념을 알아보았는데요, 그렇다면 실제로 계산은 어떻게 할까요? LDA나 QDA 계산의 핵심은 공분산행렬을 대각화하는 것입니다. QDA의 경우 각 $\hat{\Sigma_k}$ 에 대해 $\hat{\Sigma}{k} = U_k D_k U{k}^{T}$로 고유값 분해를 하는 것입니다. 이 때, $U_k$는 $p\times p$ orthonormal 행렬이며, $D_k$는 양수인 고유값 d_{kl}의 대각행렬입니다. 이렇게 되면, 판별함수 $\delta_{k}(x)$는 아래와 같이 바뀌게 됩니다.
$ (x-\hat{\mu}k)^{T}\hat{\Sigma}{k}^{-1}(x-\hat{\mu}{k}) = [U{k}^{T}(x-\hat{\mu}k)]^{T}D{k}^{-1}[U_{k}^{T}(x-\hat{\mu}_k)] $
$ log\vert \hat{\Sigma}k \vert = \sum{l}log(d_{kl})$
위 식을 바탕으로 LDA를 생각해보면 아래와 같습니다.
-
공통분산 $\hat{\Sigma} = UDU^{T}$을 고유값 분해하고, 기존의 데이터 $X$를 $X^{\ast} = D^{\frac{1}{2}}U^{T}X$로 변형시키면, 변형한 데이터 $X^{\ast}$의 공분산행렬은 단위행렬(identity matrix)가 됩니다.
-
변형된 데이터에 대해 가장 가까운 집단으로의 분류는 사전 확률 $\pi_k$에 근거합니다.
5. Reduced-Rank Linear Discriminant Analysis
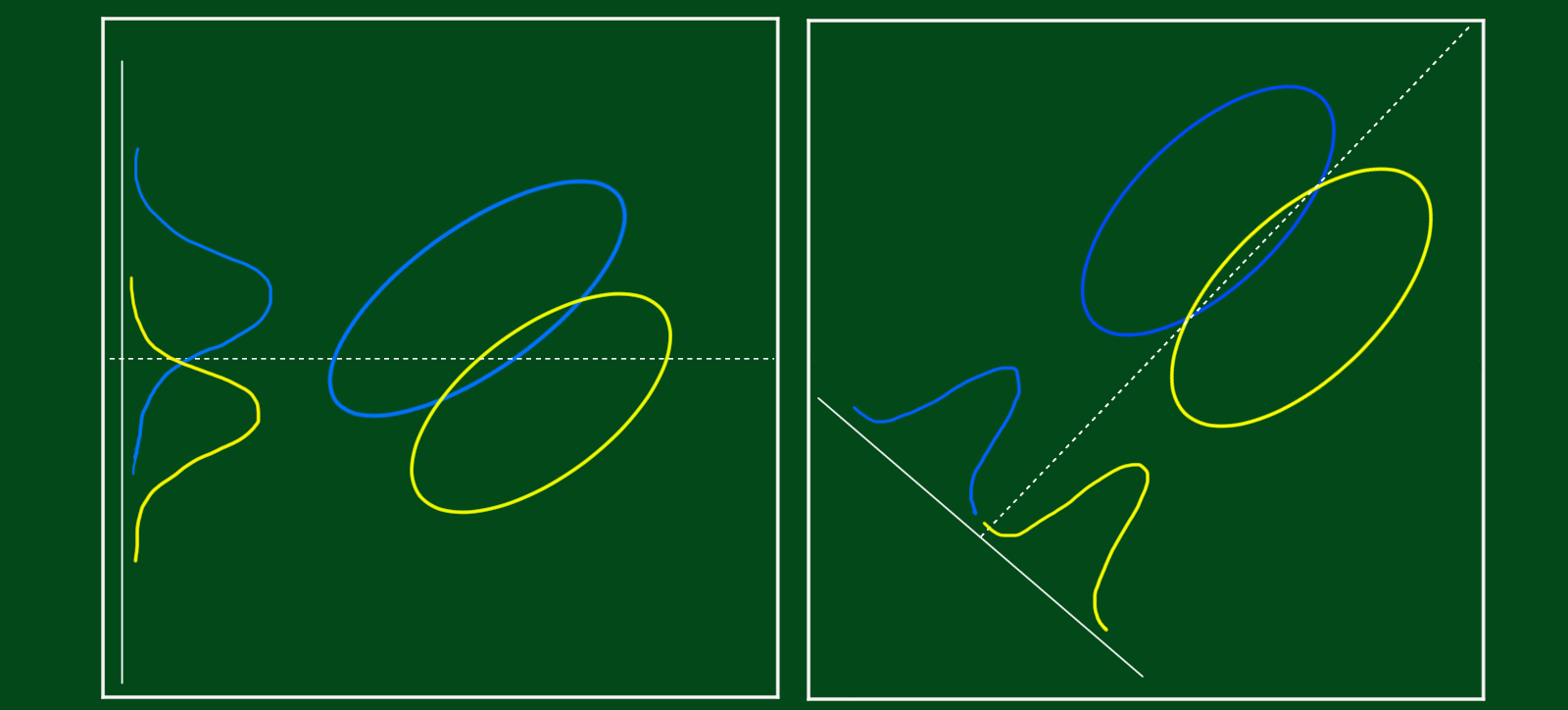
LDA에서의 차원축소란, 최대 $K-1$ 차원인 부분공간에서의 데이터를 고려하는 것입니다. 예를 들어, $K=3$인 경우, 데이터를 2차원 플랏으로 나타내고 클래스를 색깔로 구분하는 것입니다. 이 경우 데이터를 클래스별로 분류하는데 있어, 어떠한 정보손실도 없습니다. 그렇다면 $K>3$이면 어떨까요? $K>3$인 경우에는 $L<K-1$인 최적의(optimal) 부분공간을 찾아야합니다. 여기서 ‘최적의’이라는 말의 의미는 새로운 부분공간에 집단의 중심을 투영(project)했을 때, 집단 별 평균값이 최대한 멀리 떨어져있어야하고, 집단별 분산이 작아야합니다. 무슨말이냐면 투영된 집단별 평균값이 최대한 멀리 떨어져있고, 투영된 집단별 분산이 작아야 투영된 집단별 겹치는 부분이 작아집니다. 집단별 데이터가 겹치는 부분이 작아야 잘 분류되겠죠. 이때 쓰이는 값은 적절한 주성분(Principal Component)으로 구성된 부분공간을 찾는데 사용됩니다. LDA와 관련된 최적의(optimal) 부분공간을 찾는 과정은 아래와 같습니다.
-
클래스 중심(class centroid) $M$의 $K\times p$행렬 및 집단 내(within class) 공분산행렬 $W$ 계산.
-
공분산행렬 $W$를 고유값분해한 후 $M^{\ast} = MW^{-\frac{1}{2}}$ 계산
-
2에서 $M^{\ast}$의 공분산행렬을 계산한다. 이 때 구한 공분산행렬 $B$는 집단 간(between class) 공분산행렬입니다.
-
3에서 구한 공분산행렬 $B$를 고유값 분해해서 새로운 공분산행렬 $B^{\ast} = V^{\ast}D_{B}V^{\ast T}$를 계산합니다.
-
4에서 구한 $V^{\ast T}$의 각 열이 새로운 부분공간의 축이 됩니다.
위 과정을 종합하면 $l$번째 판별변수(discriminant variable)은 $Z_l = v_{l}^{T}X$입니다. 이 때, $v_l = W^{-\frac{1}{2}}v_{l}^{\ast}$ 입니다. 즉, 집단 간 분산은 최대화 시키고, 집단 내 분산을 최소화 시키는 선형조합(linear combination) $Z=a^{T}Z$을 찾는 문제라고 할 수 있겠습니다. 즉, 기존 데이터 $X$를 새로운 공간에 투영해서 새로운 데이터 $Z$가 되는 것입니다.
이 때, “집단 간” 분산이라는 말의 의미는 $Z$행렬의 클래스 평균의 분산을 의미합니다. 또한 “집단 내” 분산은 각 집단별 평균에 대한 해당 집단의 데이터의 합동분산(pooled variance)을 의미합니다.
자, 그러면 집단 간 분산을 구해보겠습니다. 변환된 데이터 $Z$의 집단 간 분산은 아래와 같습니다.
$ cov(a^{T}X) = a^{T}B a$
또한 변환된 데이터 $Z$의 집단 내 분산은 아래와 같습니다.
$ cov(a^{T}X) = a^{T}W a $
따라서 위 두 식을 종합하면, 클래스 구분없는 전체 데이터 $X$의 공분산은 집단간분산과 집단내분산의 합과 같습니다.
집단간분산을 최대화하고, 집단내분산을 최소화 시킨다는 말을 수식으로 나태내면 아래와 같습니다.
$ max_{a} \frac{a^{T}B a}{a^{T}W a}$
즉, 이 문제에서 첫번째 축은 $W^{-1}B$행렬의 가장큰 고유값을 찾는 문제와 같습니다. 두번째축은 두번째로 큰 고유값을 찾는 문제와 같죠. 이 때 구한 $a_l$은 판별좌표(discriminant coordinates)입니다. 여기서 헷갈리지 말아야할 점은 판별함수(discriminant function)과 혼동하면 안된다는 것입니다.


