[머신러닝] K-최근접 이웃 알고리즘의 개념
업데이트:
K-최근접 이웃 알고리즘의 개념
참고링크
학습(learning)의 분류
본 포스팅은 MIT 6.034 Artificial Intelligence 수업을 참고하여 작성하였습니다.
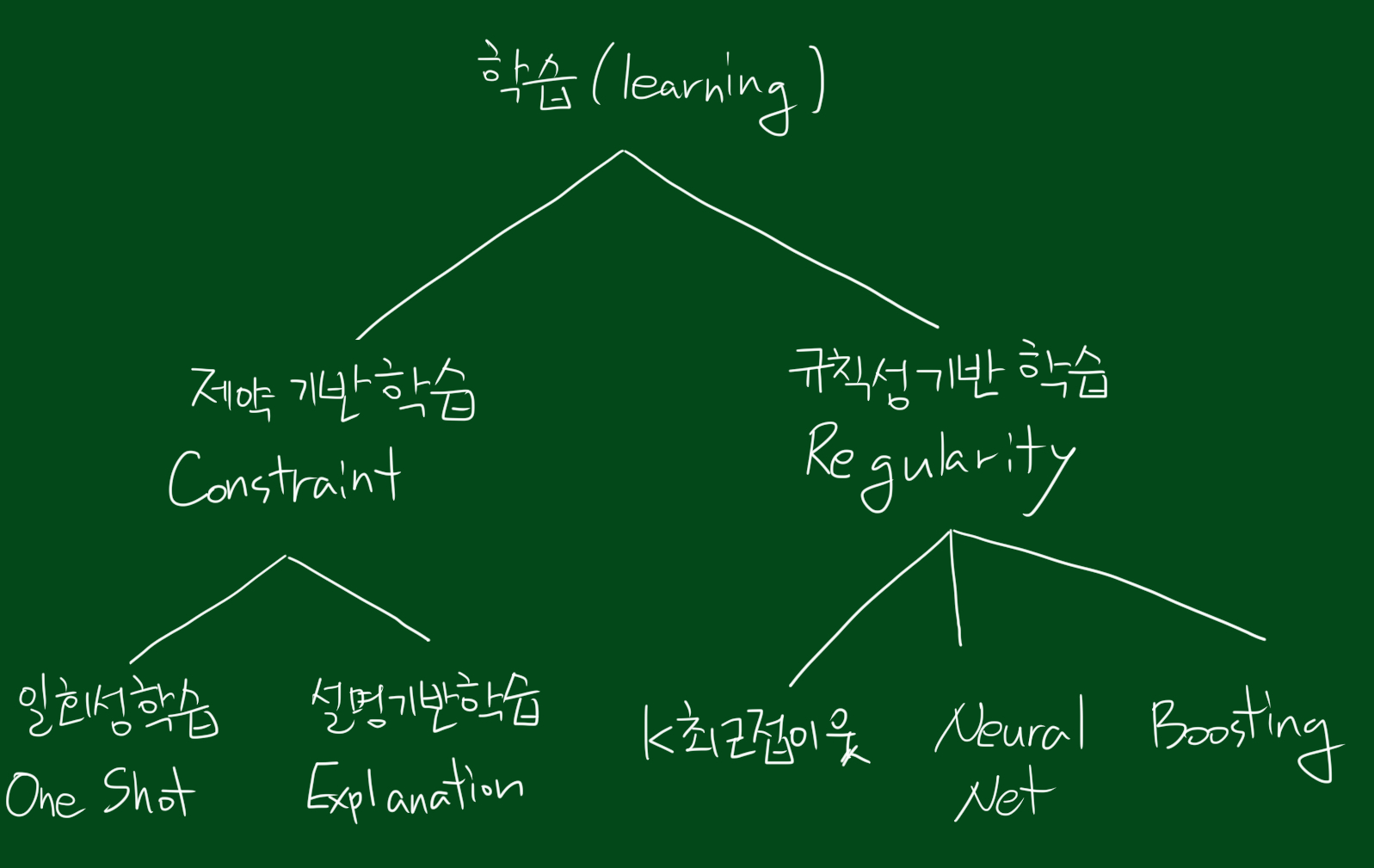
우리가 학습이라고 부르는 개념은 크게 두 갈래고 나눠집니다. 하나는 제약기반학습, 하나는 규칙성기반학습인데요, 흔히 제약기반학습은 인간과 유사한(humanlike) 학습이고, 규칙성기반학습은 마치 불도저가 자갈을 처리하듯 정보를 처리한다고해서 불도저 컴퓨팅이라고도 불립니다.
제약기반학습은 다시 일회성학습과 설명기반학습으로 나눠지는데요. 일회성학습은 오직 경험으로만 학습되는 것을 의미합니다.
규칙성기반학습은 K최근접이웃, 신경망, 부스팅으로 나눠집니다. K최근접이웃 알고리즘의 경우 패턴인식분야 학술지에서 아주 많이 사용되는 방법입니다. 또한 여러학습중 가장 간단하기 때문에 가장 먼저 시도되는 방법이기도합니다.
이에반해 신경망은 생명화학을 모방하려는 경향이 있고, 부스팅은 이론적인 경향이 있습니다.
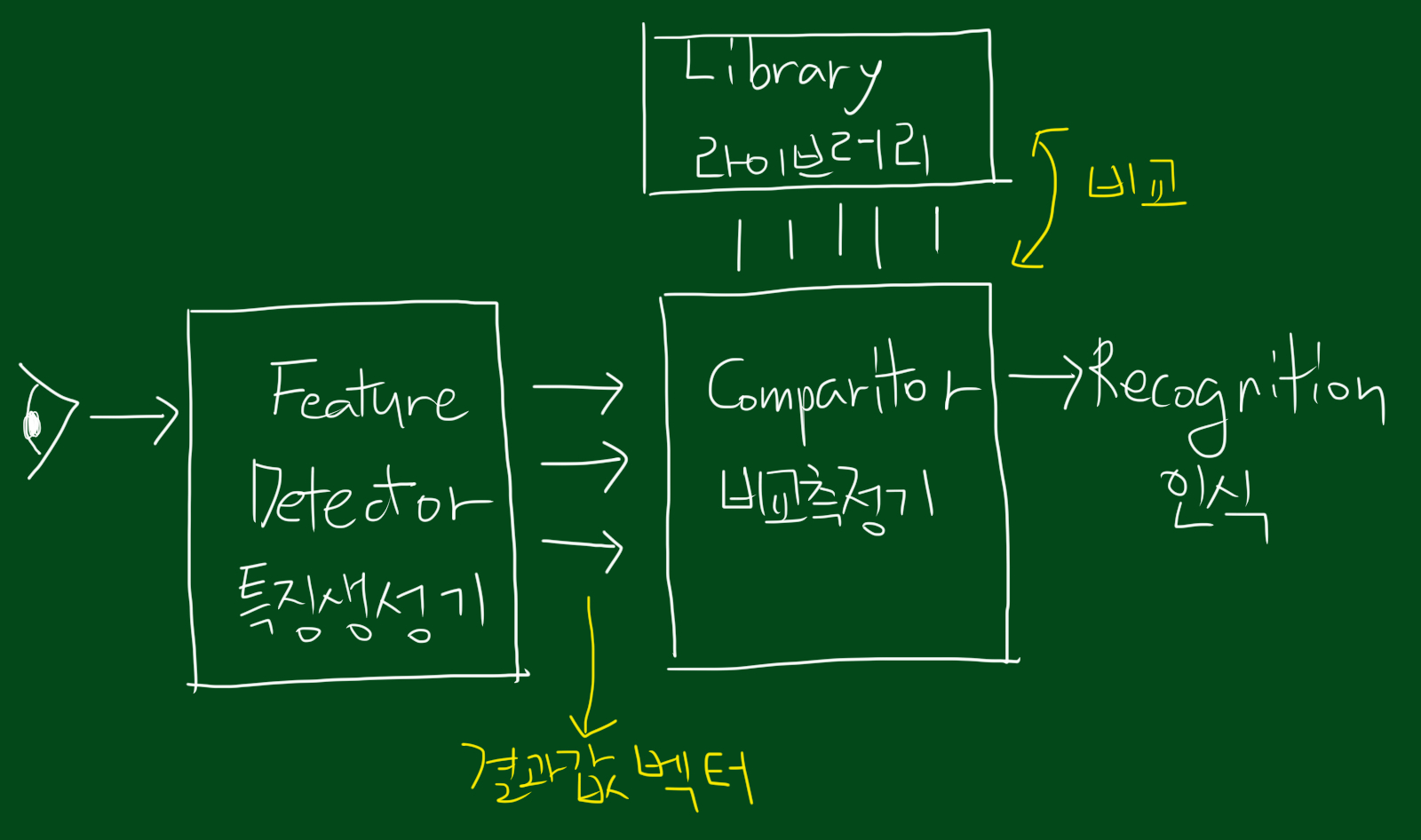
패턴인식이라는 말에 대해 잠시 살펴보면, 우리가 어떠한 것을 관측했을 때, 여러가지 특징 벡터가 특쟁생성기(feature detector)로 들어갑니다. 그리고 그 결과값 벡터들이 비교측정기로 들어가 라이브러리와 비교합니다. 그래서 어떤 것인지 인식하게 되는 것이죠.
K-최근접 이웃 알고리즘의 정의
패턴인식에서, k-최근접 이웃 알고리즘(knn)은 분류나 회귀에 사용되는 비모수 방식이다. 두 경우 모두 입력이 특징 공간 내 k개의 가장 가까운 훈련 데이터로 구성되어있다. 출력은 k-NN이 분류로 사용되었는지 회귀로 사용되었는지에 따라 다르다.
k-NN 분류에서 출력은 소속된 항목이다. 객체는 k개의 최근접 이웃 사이에서 가장 공통적인 항목에 할당되는 객체로 과반수 의결에 의해 분류된다. 만약 k=1이라면 객체는 단순히 하나의 최근접 이웃의 항목에 할당된다.
k-NN 회귀에서 출력은 객체의 특성 값이다. 이 값은 k개의 최근접 이웃이 가잔 값의 평균이다.
K-최근접 이웃 알고리즘의 기본 개념
아래와 같은 데이터를 분류한다고 생각해봅시다. 동그라미, 세모, 네모 그룹이 있을 때, 새로운 데이터인 별모양이 어느 그룹에 속하는지를 결정하는 문제입니다.
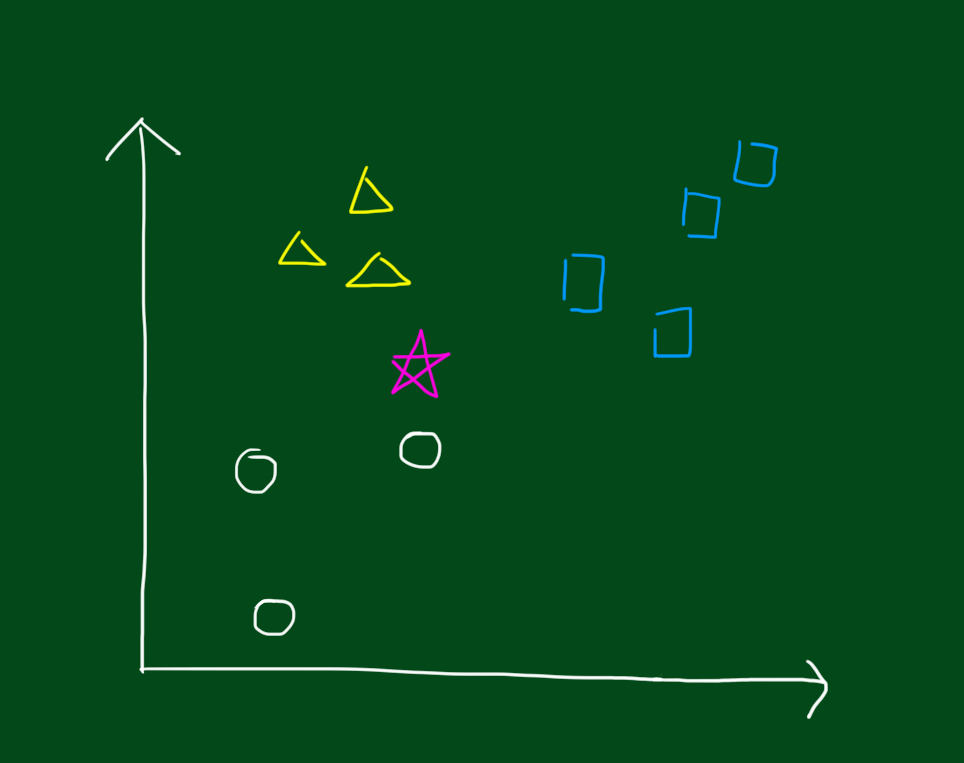
K 최근접 알고리즘은 데이터가 어느그룹에 속할지를 보기 위해 이름 그대로 k개의 최근접 데이터를 참고하는 것입니다.
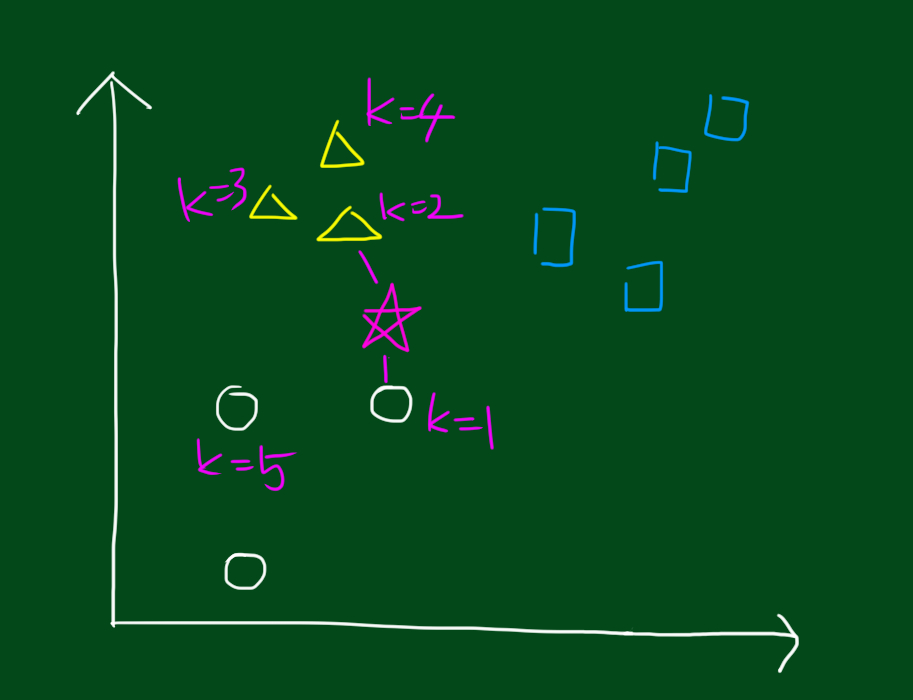
우선 1-최근접 데이터를 보면 가장 가까운 것은 위 그림대로 k=1, 즉 동그라미 입니다. 따라서 k=1로 설정하고 분석한다면 1-최근접 알고리즘에 의해 별모양은 동그라미 집단이 됩니다. 그렇다면 k=2로 하면 어떨까요? 이 경우 별모양 데이터의 2-최근접 알고리즘에 의해 세모 혹은 동그라미 집단이 됩니다. 마찬가지로 k=3일 때는 세모가 2개, 동그라미가 1개이므로 세모그룹에 속하게 되겠네요. 이것이 K-최근접 이웃 알고리즘의 기본 개념입니다.
예제1
예를 들어보겠습니다. 아래와 같이 데이터가 분포해있다고 생각해봅시다.
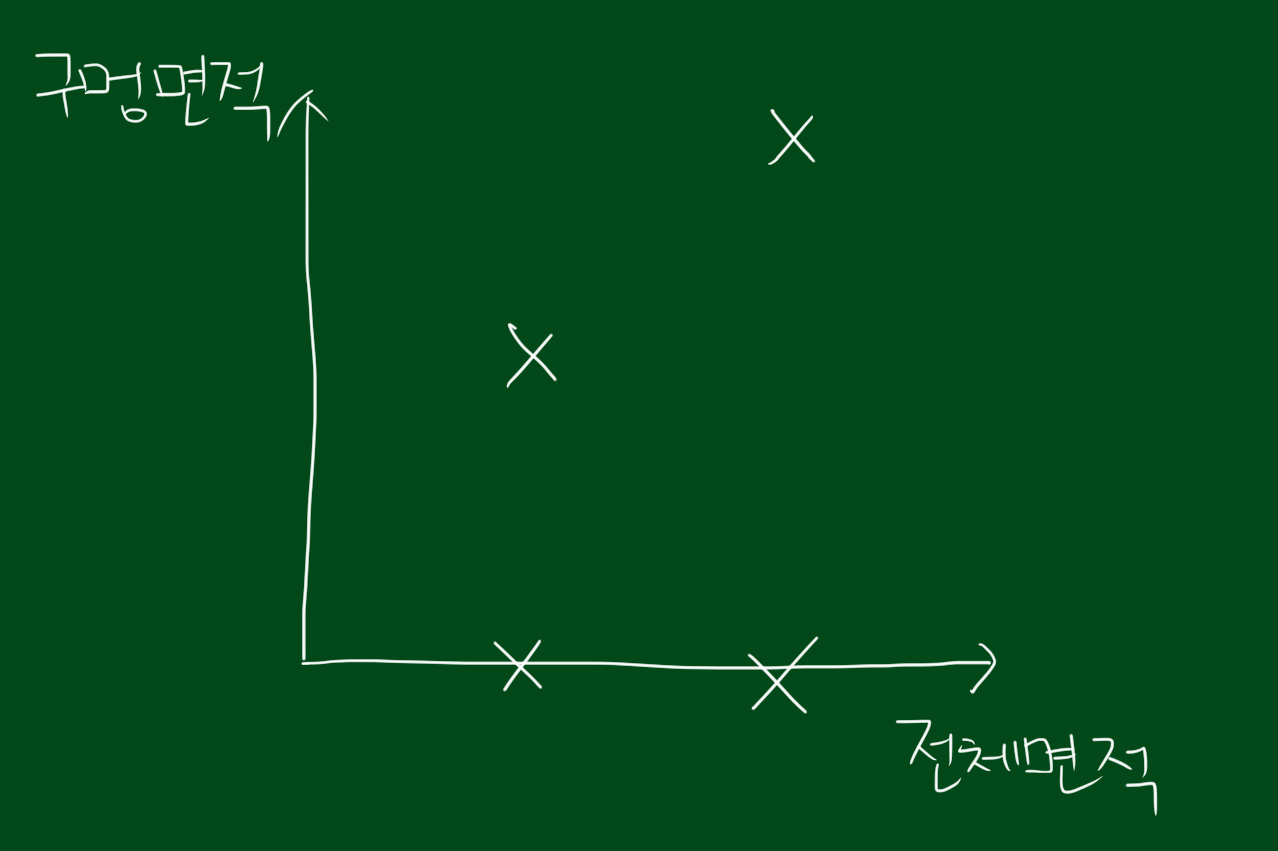
위와 같은 데이터를 어떻게 분류하면 좋을까요?
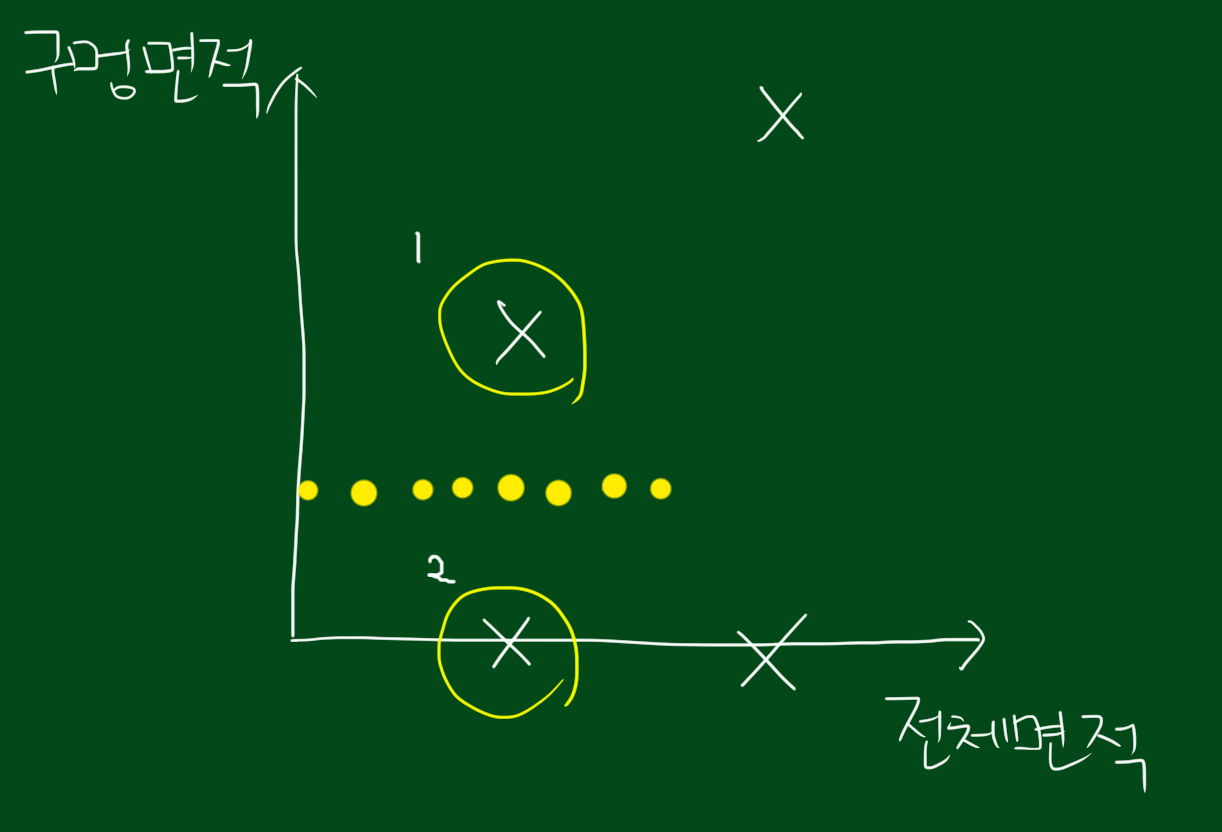
우선 1, 2데이터’만’ 고려합시다. 이 둘만 분류한다고 하면 둘 사이에 수직이등분선을 그으면 분류할 수 있을 것입니다.
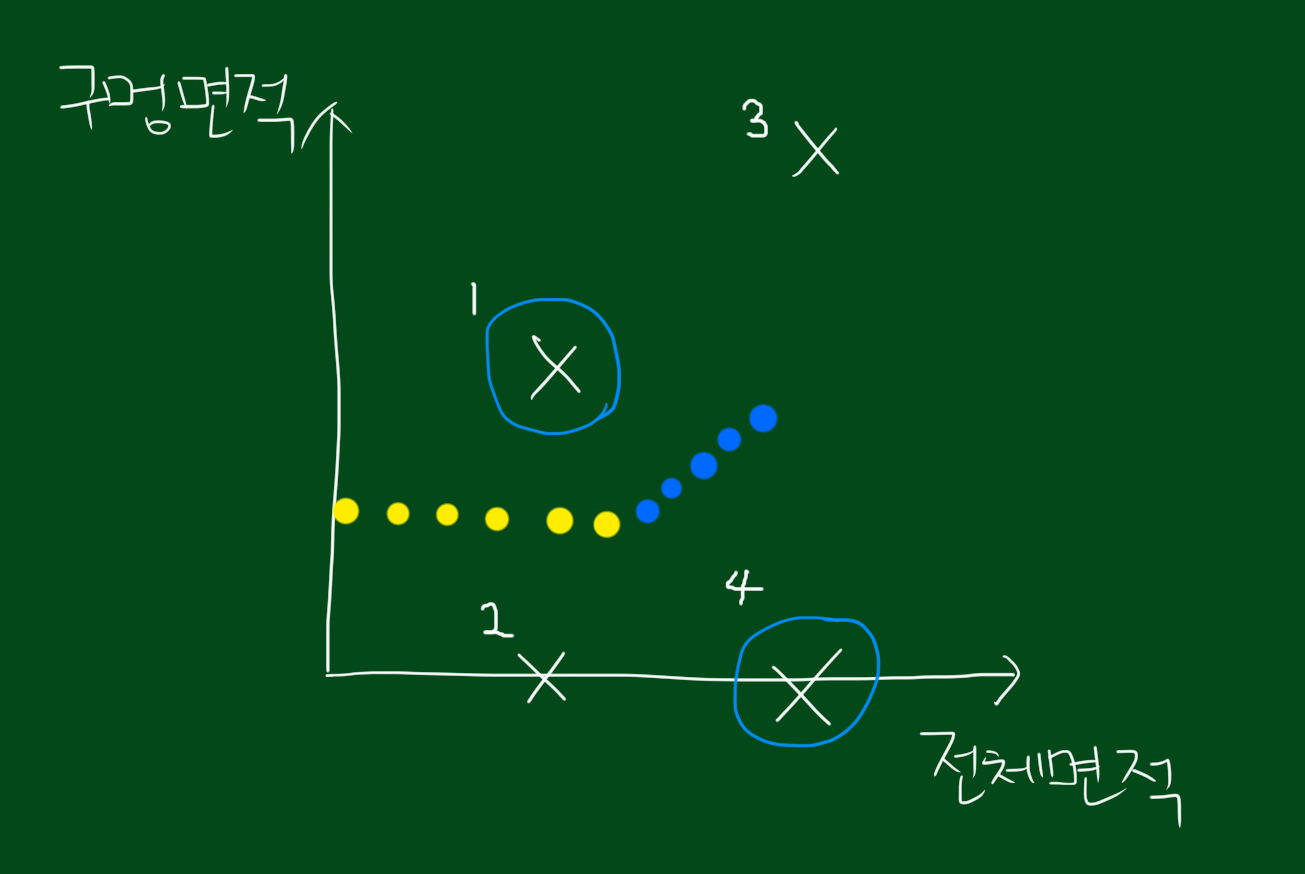
또한 1, 4데이터’만’고려하면 위와 같이 파란색 선을 그울 수 있습니다.
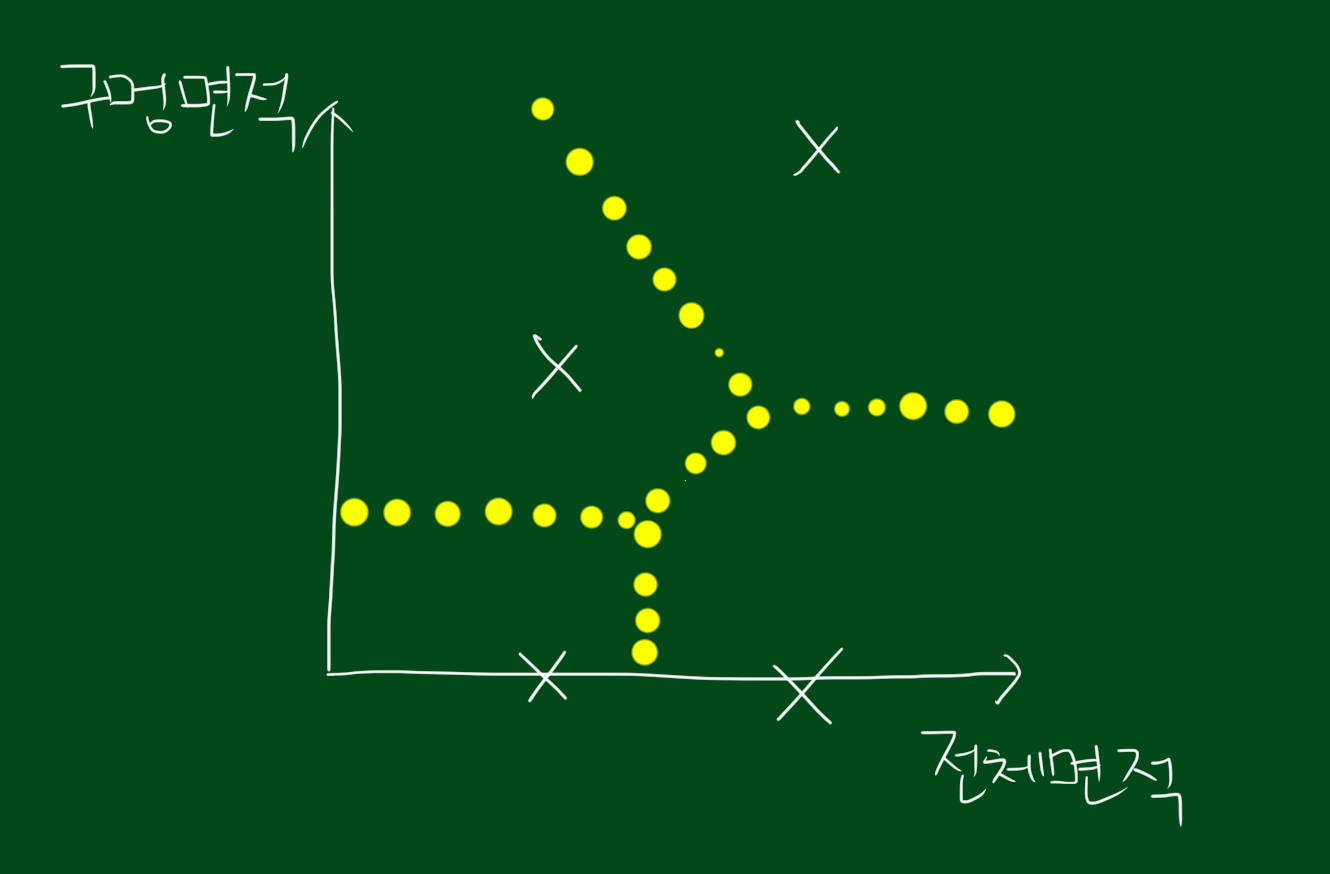
이 과정을 점들마다 반복하면 위와 같이 분류됩니다. 그럼 아래와 같이 새로운 데이터가 추가되었을 때, 이 데이터는 어느 집단에 속할까요?
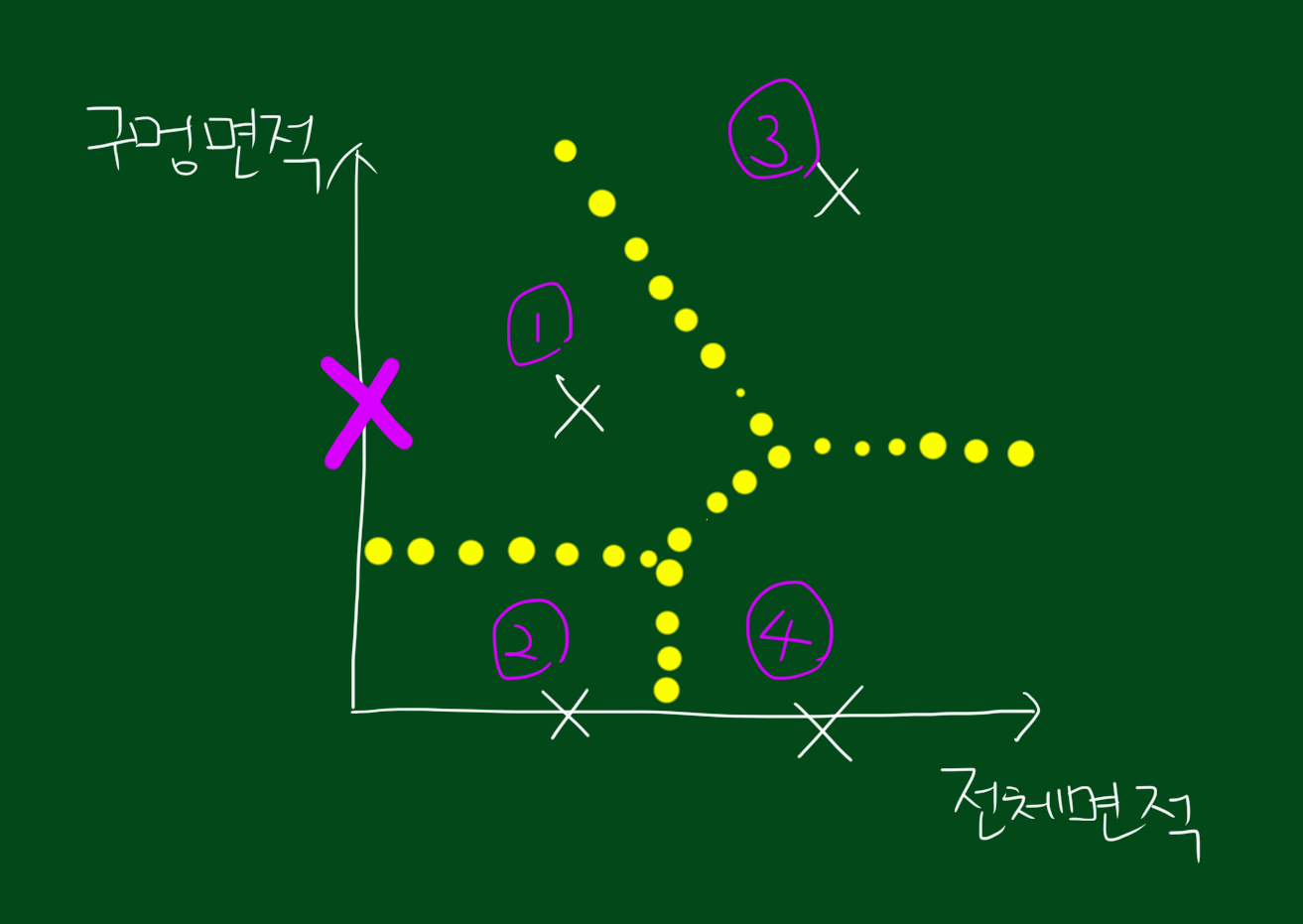
답은 1번 집단입니다. 왜냐하면 우리가 알수있는건 새로운데이터와 1데이터의 구멍면적이 비슷하다는 것을 알 수 있는데요. 어떤 면의 특징이 유사하다면 다른 면에서도 유사할 것이라는 것이 근거입니다. 이 원리는 대부분의 교육 원칙에 적용됩니다.
예제2
또다른 예제를 생각해봅시다. 여러분은 잡지기사 여러개를 가지고 있습니다. 그리고 특정문제를 다루는 방식을 배우고자 합니다. 여러분은 자신의 질문과 관련있는 기사를 어떻게 찾으시겠습니까? 이 문제는 정보검색에 관심있는 사람들이 수십년간 연구해온 문제입니다.
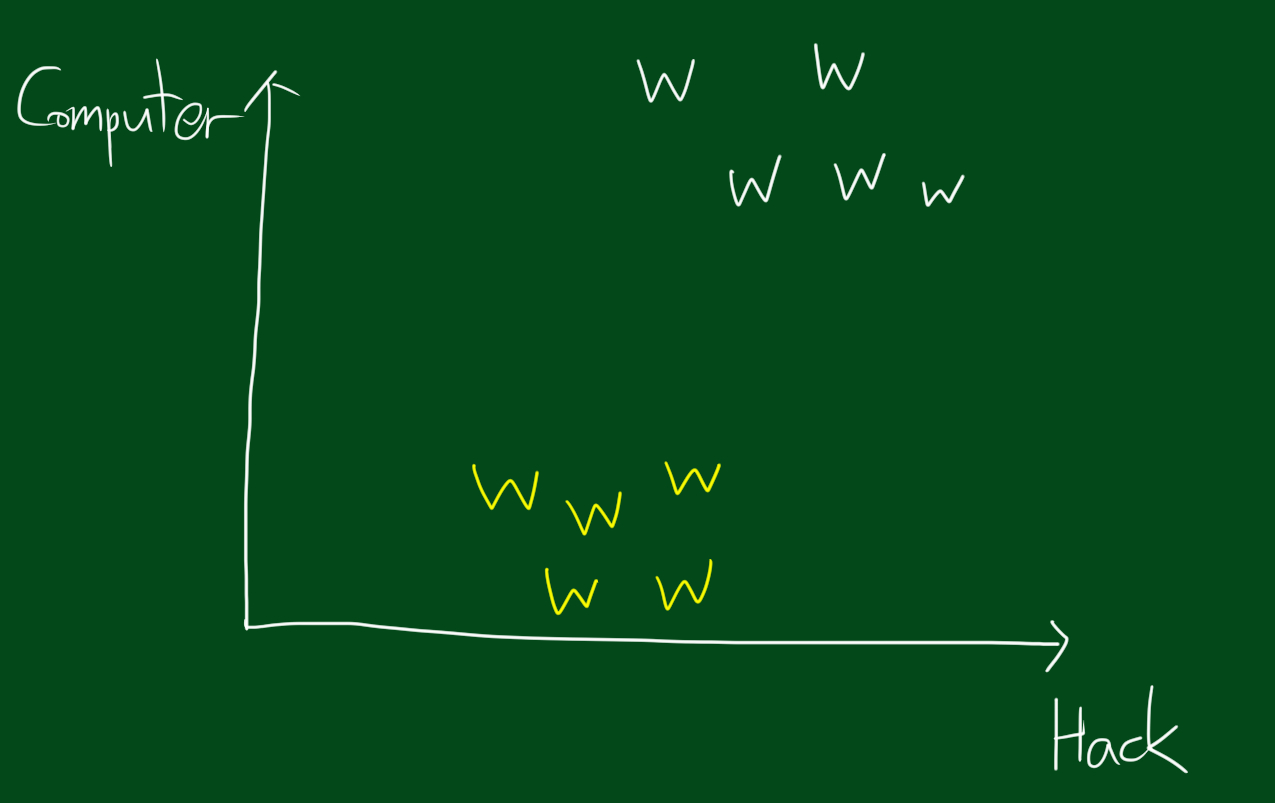
문제를 간단히 하기 위해 잡지는 두개만 고려하겠습니다. 하나는 컴퓨터공학잡지(흰색), 다른 하나는 도시와시골잡지(노란색) 입니다. 가로축은 hack이고 세로축은 computer입니다. 이때 여러분이 단어 100개에 관심있다고 했을때, 각 잡지기사의 단어수를 센 다음 그 단어수를 해결하고자 하는 질문의 단어수와 비교하면 됩니다.
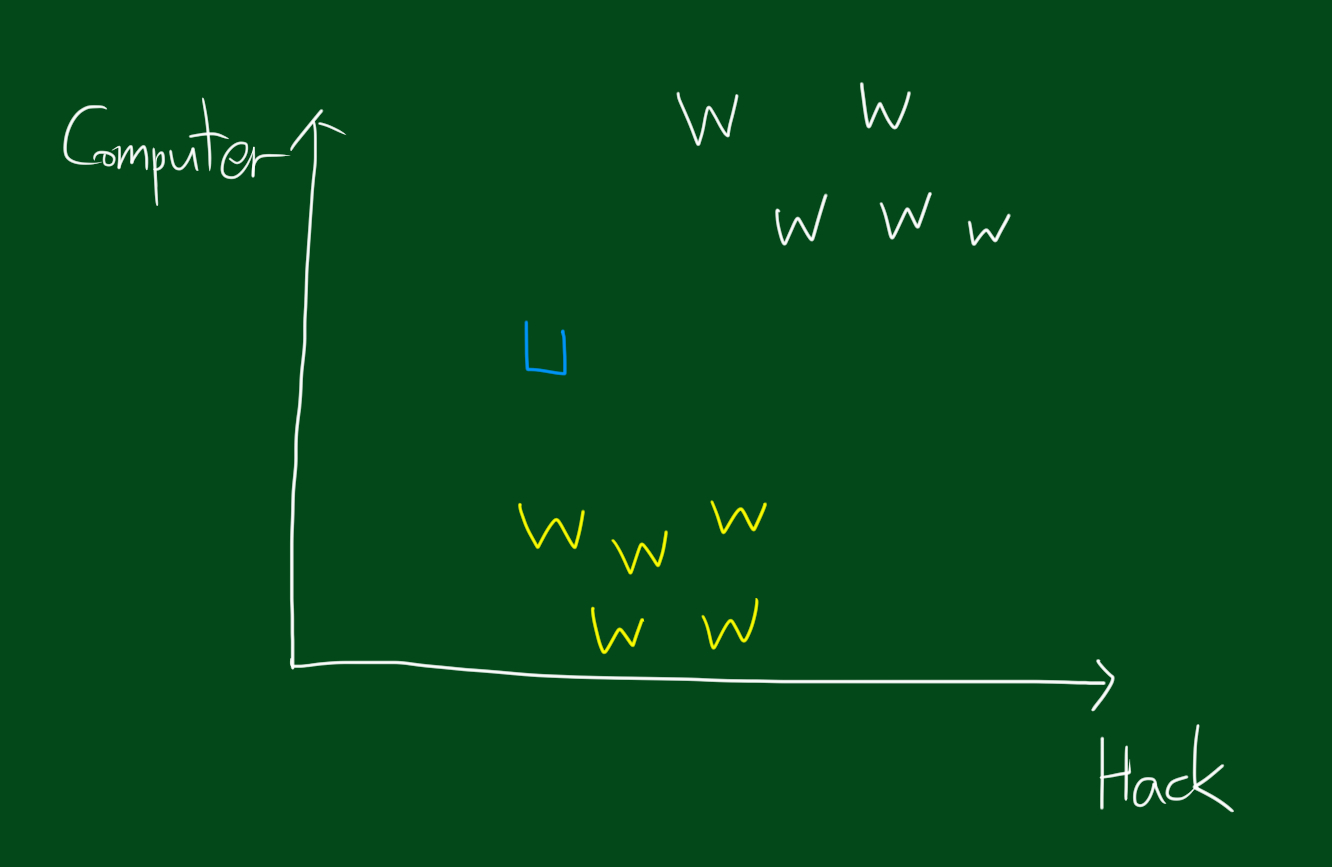
위 그림에서 여러분의 탐색질문데이터는 U(파란색) 입니다. 질문데이터는 어디와 가장 가까울까요? 그림상 보면 가장 가까운건 도시와 시골 잡지인데요, 그렇다면 k-최근접 이웃 알고리즘은 못쓰는 것일까요?
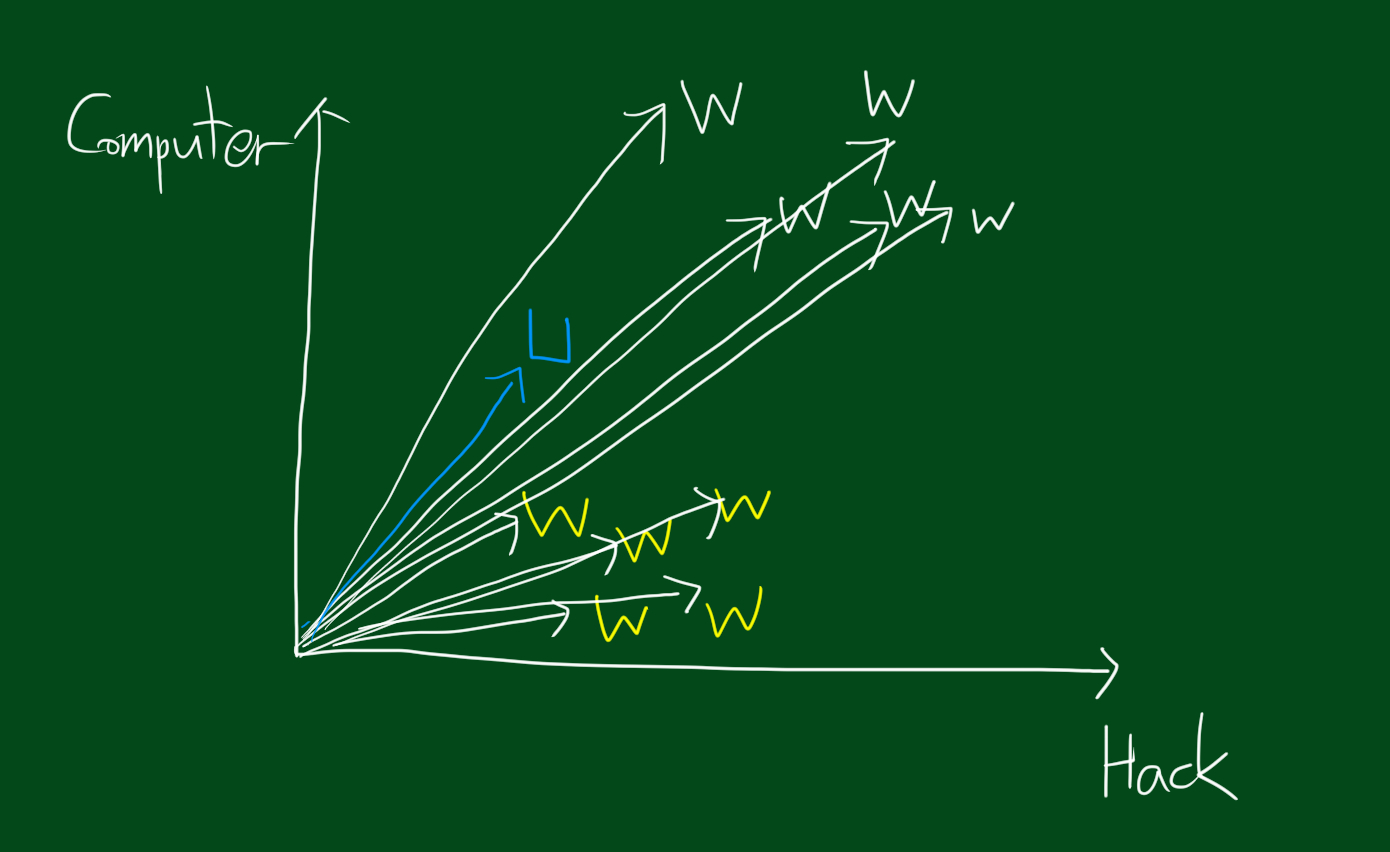
아닙니다. 이 경우에는 각 데이터들의 벡터를 고려하면 됩니다. 위 그림처럼 각 데이터를 벡터로 표시하면 U벡터가 어느 벡터와 유사한지 볼 수 있습니다. 위 그림을 보시면 탐색질문데이터는 컴퓨터공학잡지 벡터둘 사이에 있다는 것을 볼 수있는데요. 이 경우 두 개의 컴퓨터 공학잡지 벡터사이의 각도를 고려하면 됩니다. 이 부분을 좀 더 확대해보겠습니다.
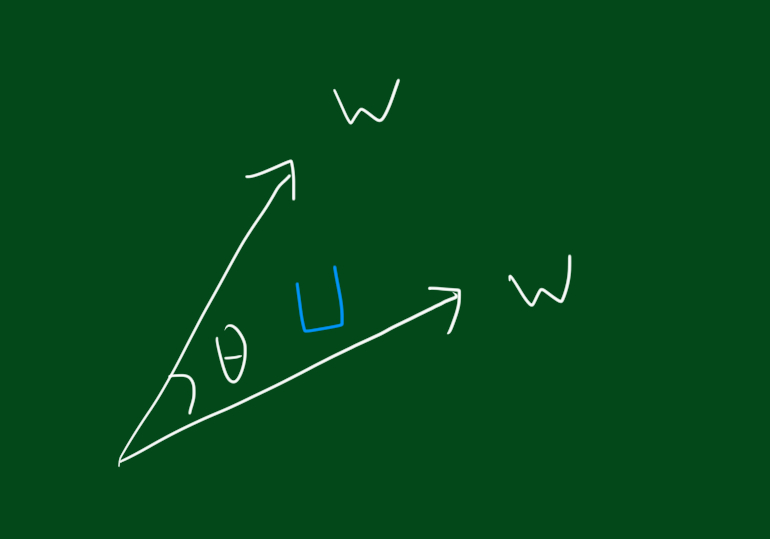
두 벡터사이의 각도로 계산하기 위해선 아래 공식을 사용합니다.
\[cos\theta = \sum \frac{U_i \times A_i}{\|U\|\|A\|}\]위 식에서 A는 기사(article) 벡터라고 보시면 됩니다. 그리고 위 식에 의해 U벡터가 다른 기사의 벡터와 같다면 코사인값은 1이 됩니다.


