[선형대수] 기저(basis)의 의미
업데이트:
기저(basis)의 의미
참고링크
기저(basis)란 무엇일까요. 위키백과를 찾아보면 아래와 같은 설명이 나옵니다.
선형대수학에서, 어떤 벡터 공간의 기저(basis)는 그 벡터 공간을 선형생성하는 선형독립인 벡터들이다. 달리 말해, 벡터 공간의 임의의 벡터에게 선형결합으로서 유일한 표현을 부여하는 벡터들이다.
지금부터 위 설명이 무엇을 뜻하는지 알아봅시다.
1.집 주소에 대한 비유
흔히 자신의 집 주소를 이야기할 때 아래와 같이 말하는 사람이 있다고 가정해 봅시다.
- 경기도 부천시 무슨동
- 수원시 청주시 과천시
우리는 보통 1과 같이 이야기하지, 2처럼 말하는 사람은 아직까지 한 번도 본적이 없습니다. 그렇다면 1과 2는 무슨 차이가 있을까요? 주소 1을 들었을 때는 본인이 지구상에 어디에 위치하는지에 대한 정보를 얻을 수 있습니다. 반면 주소 2를 들었을 때는 저 사람이 어디에 사는지 알 수 없습니다. 왜냐면 애초에 수원시와 청주시가 동시에 표현되는 것 자체가 불능이기 때문입니다. (주소가 여러 개인 경우는 제외하겠습니다.) 주소 1을 다시 보시면 경기도와 부천시는 동시에 표현할 수 있습니다. 왜냐면 ‘도’라는 기저를 이용해서 표현한 좌표가 경기도이고 ‘도시’라는 기저를 사용해 나타낸 좌표가 부천시이기 때문입니다. 따라서 주소 2에서 ‘도시’라는 기저를 사용해 나타낸 수원시, 과천시의 경우는 말이 안되는 것을 알 수 있습니다. 왜냐면 어느 한 사람의 주소가 수원시이자 과천시 일 수는 없거든요. 요약하면 집 주소를 구성하는 기저는 ‘도’, ‘시’, ‘동’이라고 할 수 있습니다. (이해를 돕기 위해, 특별시, 광역시, 구의 개념은 생략했습니다 ^^;)
2. 좌표평면에서의 기저
2차원 좌표평면을 생각해봅시다. 이 좌표평면을 구성하는 기저는 무엇일까요?
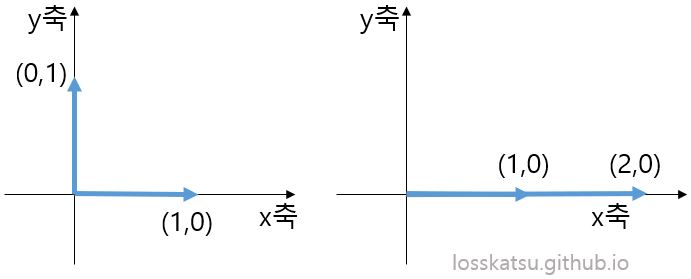
좌측, 우측의 벡터쌍을 행렬(matrix)로 표현하면 아래와 같습니다.
\[(1) \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, (2) \begin{bmatrix} 1 & 2 \\ 0 & 0 \end{bmatrix}\]이 두 행렬은 좌표평면을 나타내는 기저가 될 수 있을까요? (1)의 경우는 기저가 될 수 있지만, (2)는 기저가 될 수 없습니다. 위 그림을 보고 설명 드리자면, (1)을 구성하는 벡터조합을 이용하면 좌표평면 내의 모든 점을 나타낼 수 있습니다. 예를 들어 $(5,3)$이라는 점을 표현하고 싶다면, $5(1,0) + 3(0,1) = (5,3)$으로 표현 가능합니다. 하지만 (2)를 이용하면 벡터는 두 개지만 표현할 수 있는 건 $x$축이 전부 입니다. 벡터는 두 개지만 $(2,0)$벡터는 $2(1,0)$처럼 첫번째 벡터로 표현할 수 있으므로, 실상은 기저벡터가 하나있는 것과 다름 없습니다. 따라서 (2)를 구성하는 벡터조합을 이용하면 $(5,3)$을 표현할 수 없습니다.
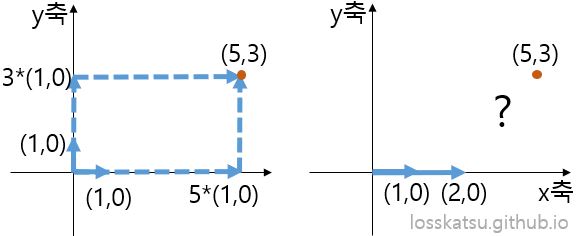
3. 기저는 유일(unique)한가요?
그렇다면 좌표평면을 구성하는 기저는 아래 행렬이 유일할까요?
\[\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\]그렇지 않습니다.
$(1,0),(0,1)$ 뿐만 아니라, $(2,0),(0,2)$ 등 $(x,0),(0,y)$ 꼴이라면 모두 기저가 될 수 있습니다. 하지만 기저를 구성하는 벡터의 수는 유일합니다. 좌표평면을 구성하는 기저벡터는 2개가 입니다. 이는 차원(dimension)과 관련있는데 이는 다음 포스팅에서 다루겠습니다.
마지막으로 기저의 정의를 다시 보면서 포스팅 마치겠습니다.
선형대수학에서, 어떤 벡터 공간의 기저(basis)는 그 벡터 공간을 선형생성하는 선형독립인 벡터들이다. 달리 말해, 벡터 공간의 임의의 벡터에게 선형결합으로서 유일한 표현을 부여하는 벡터들이다.


