[기초통계] 포아송분포 의미 및 개념 정리

포아송분포 의미 및 개념 정리

참고링크

머신러닝	딥러닝	선형대수	기초통계	최적화
k-means	신경망이란	고유값,고유벡터	확률변수	컨벡스 셋
k-최근접이웃	성능함수	행렬식	확률분포	컨벡스 함수
선형회귀	신경망 학습	내적	모집단과 표본	라그랑주 듀얼
로지스틱회귀	교차연결	기저	평균과 분산	KKT 조건
릿지,라쏘회귀	합성곱 신경망	랭크, 차원	공분산, 상관계수	ROC 커브
의사결정나무	배치, 에포크 차이	선형변환	최대가능도추정	크로스 밸리데이션
서포트벡터머신	텐서플로기초(1)	직교행렬	베르누이,이항분포	실루엣 스코어
원클래스 SVM	텐서플로기초(2)	고유값분해	기하,음이항분포
LDA	seq2seq	특이값분해	초기하분포
GMM	opencv기초		포아송분포
부스팅	resnet		정규분포
사이킷런 실습	다각형내부판별		감마분포
	엣지판별		지수분포
			카이제곱분포
			베타분포
			균일분포

1. 포아송분포 정의

포아송분포(poisson distribution)는 확률론에서 단위 시간 안에 어떤 사건이 몇 번 발생할 것인지를 표현하는 이산확률분포이다.

2. 포아송분포의 확률밀도함수, 평균, 분산

포아송분포의 확률밀도함수, 평균, 분산은 다음과 같습니다.

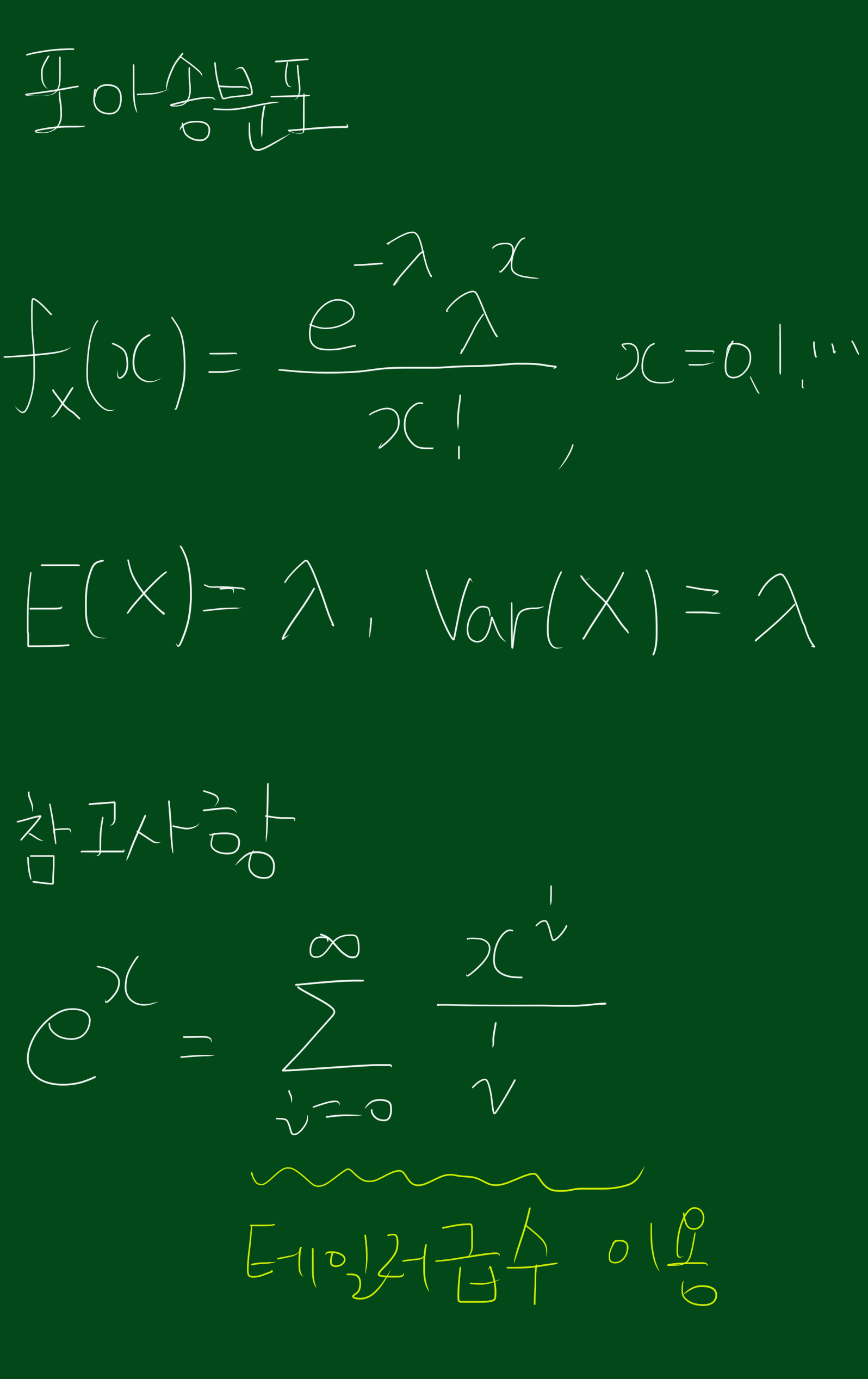
3. 포아송분포의 예

• 10시에서 11시 사이에 xx은행에 방문한 고객의 수
• 남부고속도로에서 2시에서 3시 사이에 톨게이트를 통과하는 차량의 수
• 1년 동안 특정 진도 이상의 지진 발생 횟수

4. 포아송분포 vs 이항분포

이항분포를 따르는 분포에서 시행횟수 n이 아주 커지고, p가 아주 작을 경우, 이항분포는 포아송분포로 근사시킬 수 있습니다. 따라서 처음에 이항분포를 써야하는 가정에서 n이 아주 크고 p가 아주 작다면 포아송분포를 사용하는 것이 좋습니다.

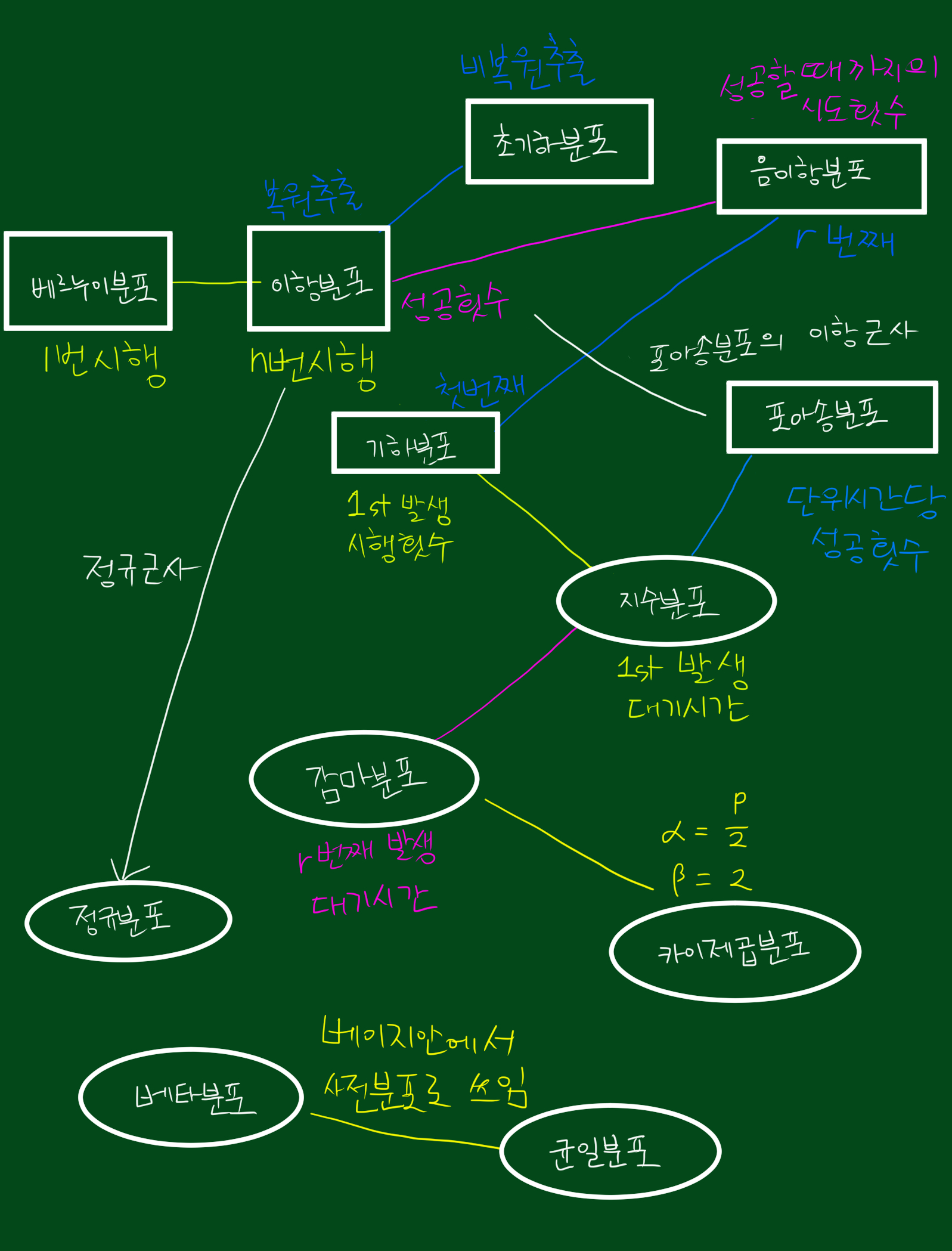
참고. 확률분포간 관계도