[선형대수] 고유값(eigenvalue) 고유벡터(eigenvector)의 의미
업데이트:
고유값(eigenvalue) 고유벡터(eigenvector)
참고링크
저는 선형대수에서 가장 중요한 부분으로 고유값, 고유벡터를 꼽겠습니다. 고유값, 고유벡터는 선형대수 전체를 아우르는 중요한 개념이라고 생각합니다. 일반적인 선형대수 책에서 고유값, 고유벡터를 찾으면 다음과 같은 정의을 아주 쉽게 찾아 보실 수 있습니다.
$ Ax = \lambda x$
$\lambda$가 실수 공간에 속할때($\lambda \in R$), 정방행렬(square matrix) $A$의 고유벡터는 영벡터가 아닌 벡터(nonzero vector) $x$이다. 또한, $\lambda$는 $A$의 고유값이다.
이 정의가 의미하는 바는 무엇일까요? 아마 교과서 정의 만으로는 이해하기 어려울 수 있습니다.
지금부터 저와함께 차근차근 그 의미를 알아봅시다.
먼저 정방행렬 $A$의 의미를 알아봅시다.
정방행렬 A의 의미
우리가 알고 있는 행렬에는 여러가지 의미가 포함되어 있지만, 고유값, 고유벡터를 논할 때, 정방행렬은 선형변환을 의미합니다. 그렇다면 선형변환은 무엇일까요?
선형변환의 의미
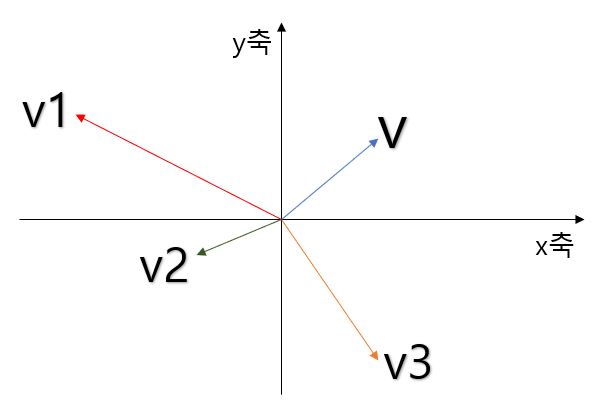
선형변환은 쉽게 말해서 좌표공간 내에서 일어날 수 있는 모든 변환이라고 생각하시면 편합니다. 예를 들어, 좌표평면에 벡터 하나가 있다고 가정하면, 그 벡터를 확대하거나, 축소하거나, 회전시키거나, 반사시키는 것은 모두 변환이라고 생각할 수 있습니다. 물론 엄밀하게 말하면 이는 틀린 설명이라고 할수도 있으나, 처음 접하실때는 이렇게 이해해도 문제 없다고 생각합니다. 아래 그림에서 원본 벡터 v는 다양한 선형변환을 통해 v1, v2, v3로 변환될 수 있습니다.
Ax의 의미
결국 Ax 는 x라는 벡터에 선형변환(A)을 취한 것을 의미합니다. 벡터 x를 늘리거나 줄이거나 회전시키거나 하는 등 어떤 ‘변환’을 취한 것이지요.
‘고유’, ‘벡터’의 의미
벡터라는 단어는 많이 들어보셨을 거라 생각합니다. 벡터를 구성하는 요소에는 두 가지가 있습니다. 여러분도 잘 알다시피 ‘방향(direction)’과 ‘크기(magnitude)’ 가 그것입니다.
고유, 즉 eigen은 어떤 뜻일까요? eigen은 독일어 인데, “own”, “peculiar to”, “characteristic”, “individual”이라는 뜻입니다. 여러분은 이 단어들 중 어떤 단어가 끌리시나요? 저는 characteristic 이라는 단어가 끌립니다. 만약 여러분이 책을 보다가 characteristic 이라는 단어가 나온다면 집중하실 필요가 있습니다. characteristic은 여러 분야에서 중요한 뜻으로 쓰이더라구요. characteristic은 무슨 뜻일까요? 네이버 영어사전을 찾아보니 “특유의”, “특징” 이라는 뜻이 나오네요. 따라서 고유벡터란 어떤 특징을 가지고 있는 벡터라는 것으로 추측할 수 있습니다. 여기서 말하는 특징은 방향(direction)은 변하지 않고, 크기(magnitude)만 변하는 특징을 말합니다. 즉, 고유벡터란 어떤 선형변환을 취했을 때, 방향은 변하지 않고 크기만 변하는 벡터를 의미 합니다.
고유값의 의미
앞서 고유벡터의 크기가 변한다고 했는데, 얼마나 변할까요? 바로 그 변한 크기가 고유값을 뜻합니다. 만약 고유값이 2라면 기존벡터 크기의 2배만큼 길어진 것이고, 고유값이 1/3 이라면 기존 벡터 크기의 1/3 만큼 줄어든 것이지요.
고유값, 고유벡터의 의미
마지막 정리입니다. 고유벡터란 어떤 벡터에 선형변환을 취했을때, 방향은 변하지 않고 크기만 변환되는 벡터를 의미하고, 고유값이란 고유벡터가 변환되는 ‘크기’를 의미합니다.