[선형대수] 행렬식(determinant)의 의미
업데이트:
행렬식(determinant)의 의미
참고링크
위키백과에서 행렬식을 검색하면 아래와 같은 결과가 나옵니다.
선형대수학에서, 행렬식(determinant)은 정사각행렬에 수를 대응시키는 함수의 하나이다. 대략, 정사각행렬이 나타내는 선형변환이 부피를 확대시키는 정도를 나타낸다.
1. determinant
행렬식은 영어로 determinant라고 합니다. 영어사전에서 determinant를 찾아보면, ‘결정요인’ 이라는 뜻이 나옵니다. 잘은 모르겠지만 뭔가 ‘결정적인 역할을 하는’ 느낌이 듭니다. 행렬식은 과연 무엇을 결정할까요?
2. 2 by 2 행렬
먼저 간단하게 $2 \times 2$ 행렬을 살펴봅시다.
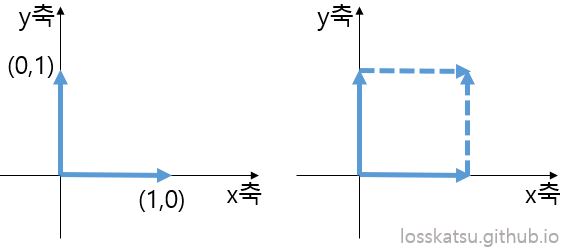
\[\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\]첫 행렬로 (1, 0), (0, 1) 두 벡터로 구성된 행렬을 봅시다.
이 두 벡터를 좌표공간에 표현하면 아래 그림의 좌측과 같은 형태로 그릴 수 있습니다.
그리고 두 벡터를 이용해 만들 수 있는 우측 도형의 면적이 해당 행렬의 행렬식의 절대값 입니다.
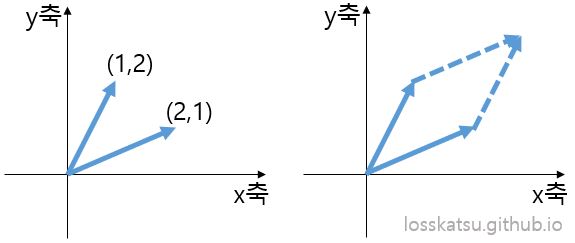
예를 하나만 더 들어볼께요. (2, 1), (1, 2) 두 벡터로 구성된 행렬을 봅시다.
\[\begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}\]이 벡터로 구성된 도형은 평행사변형이네요.
마찬가지로 행렬식의 절대값은 이 도형의 면적을 의미합니다.
3. 3 by 3 행렬
위 섹션의 개념을 한 차원 확장시키면 바로 $3 \times 3$ 행렬식의 의미를 파악하실 수 있습니다. 네, $3 \times 3$ 행렬식의 의미는 3차원 공간에서 해당 행렬 속 벡터들로 구성된 3차원 도형의 부피를 의미합니다.
4. n by n 행렬
따라서 $n \times n$ 행렬의 행렬식은 n차원 공간의 벡터들로 구성된 도형의 부피라는 것을 알 수 있습니다.
5. 행렬식(determinant)의 의미
앞서 말한 내용을 정리하면 행렬식의 절대값은 ‘부피’라고 생각할 수 있습니다.
이 사실로부터 개념을 조금 확장시켜보면, 행렬식이 0이라는 것은 어떤 의미일까요?
행렬을 구성하는 벡터가 영벡터가 아닌데 각 벡터로 구성된 도형의 부피가 0이라는 사실은
행렬을 구성하는 벡터가 서로 동일선상(colinear)에 있다는 것을 의미합니다.
이는 행렬의 구성하는 벡터가 해당 공간의 기저가 아님을 의미하는데
이는 나중에 기저와 차원을 다룰 때 자세히 설명하도록 하겠습니다.
이 개념을 생각하면 행렬식의 여러가지 특징을 이해할 수 있습니다.
예를 들어 행렬을 구성하는 행이나 열의 순서를 바꾸어도 행렬식의 절대값은 바뀌지 않습니다.
이는 벡터의 순서를 바꾸어도 공간을 구성하는 벡터의 순서만 바뀔뿐 벡터가 구성하는 도형의 부피는 바뀌지 않기 때문입니다.
또한 $det(AB) = det(A)det(B)$ 라는 성질의 의미는 다음과 같습니다.
행렬 $A$를 선형변환이라고 생각하고 행렬 $B$를 기존의 도형이라고 생각하면
행렬 $B$를 선형변환했을때의 부피를 $det(AB)$라고 생각할 수 있다고 생각합니다(좌변).
그럼 우변은 어떨까요? $det(A)$는 선형변환 기저의 부피라고 생각할 수 있고 $det(B)$를 곱함으로써
선형변환 이후의 부피, 즉 좌변과 같아진다고 볼 수도 있을 것 같습니다.
마지막으로 위키백과 정의를 다시 보면서 이 글을 마치도록 하겠습니다.
선형대수학에서, 행렬식(determinant)은 정사각행렬에 수를 대응시키는 함수의 하나이다. 대략, 정사각행렬이 나타내는 선형변환이 부피를 확대시키는 정도를 나타낸다.


