[딥러닝] ResNet의 개념
업데이트:
딥러닝 - ResNet의 개념
참고링크
설치 링크
- 윈도우에 아나콘다를 사용해 파이썬 가상환경 설치하기
- 맥북에 파이썬 가상환경(pyenv) 설치하기
- 우분투에 파이썬 가상환경(pyenv) 설치하기
- CentOS에 파이썬 가상환경(pyenv) 설치하기
- 아나콘다 32비트 가상환경 설치하고, 키움 api 연동
1. 기존 신경망의 문제점
인공지능 부야에서 뉴럴 네트워크 신경망은 정확도를 향상시키는데 큰 도움이 되었습니다. 신경망에는 여러 종류가 있는데 이미지 처리를 할떄는 CNN(Convolutional Neural network)이 주로 사용되고, 자연어 처리를 할때는 RNN(Recurrent Neural network)가 주로 사용됩니다. 이들 신경망으로 학습을 시키면 훌륭한 결과를 보여주지만 단점이 전혀 없는 것은 아닙니다. 그것은 바로 신경망의 레이어가 커지면 데이터를 학습시키기 어렵다는 단점이 있습니다. 그 이유는 신경망의 레이어가 깊어지면 vanishing gradient problem 때문에 error가 증가하기 때문입니다.
2. vanishing gradient problem
오차역전파(backpropagation), 그래디언트(gradient)기반의 학습 방법은 모두 이런 문제를 가지고 있습니다. 왜냐면 오차역전파나 그래디언트 방법을 쓰게 되면 신경망의 가중치(weight)를 업데이트하게 되는데, 업데이트 하게 되는 과정에서 gradient 자체가 매우 작아지는 vanishing 문제가 생깁니다. 이러한 문제를 해결하기위해 만들어진 것이 ResNet(Residual neural network) 입니다.
3. ResNet
3.1. 입력값과 출력값의 차원이 동일한 경우
그렇다면 ResNet이란 무엇일까요? ResNet은 Residual neural network의 줄임말인데, 이름을 보면 잔차(residual)과 관련이 있다는 것을 알 수 있습니다. ResNet을 사용하면 레이어의 인풋이 다른 레이어로 곧바로 건너 뛰어 버립니다. 즉, 인풋 값들이 중간의 특정 레이어들을 모두 거치지 않고 한번에 건너 뛴다는 의미입니다. 이를 그림으로 나타내면 다음과 같습니다.
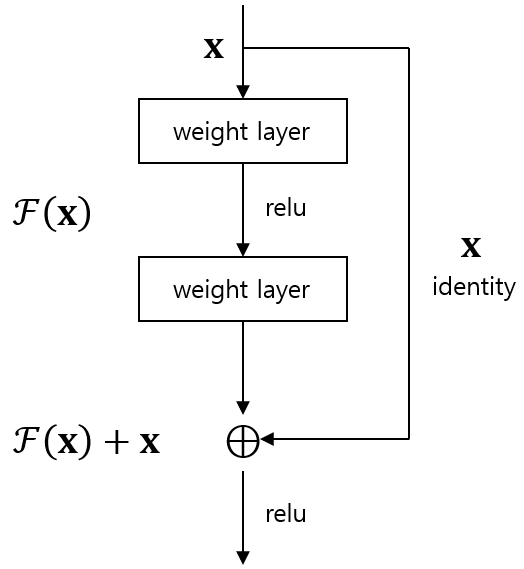
위 그림이 ResNet을 가장 잘 나타내는 그림입니다. 그림을 잘보면 신경망의 입력값은 x인데 이 입력값 x가 가중치 레이어를 거쳐서 만들어지는 값이 F(x)입니다. 그리고 오른쪽을보면 그냥 입력값 x자체가 레이어를 거치지 않고 그대로 건너 뛰는데 이를 identity mapping이라고 합니다. identity mapping은 입력값과 출력값이 같은 매핑을 의미합니다. identity mapping은 skip connection 또는 identity shortcut connection이라고도 부릅니다. 따라서 x라는 입력값이 신경망을 거치고 난 결과는 가중치를 거친 값 F(x)와 identity mapping을 거쳐 만들어진 x 더한 F(x)+x가 됩니다. 따라서 최종 출력값이 y라고 하면 y는 다음과 같이 쓸수 있습니다.
y = F(x)+x
이것이 가장 간단한 형태의 ResNet입니다.
3.2. 입력값과 출력값이 동일하지 않은 경우
위와 같은 경우는 입력값과 출력값이 동일한 차원일 때 해당하는 기본적인 ResNet 입니다. 이번에는 가중치 레이어를 거친 결과와 identity mapping의 차원이 다를 경우를 생각해보겠습니다. 예를 들어 CNN의 경우 입력값을 가중치 레이어에 넣고 합성곱을 하게 되면 입력 이미지 크기가 줄어들게 되는데 이렇게 되면 줄어든 이미지 결과(F(x))와 기존 이미지 x의 행렬 크기가 달라서 덧셈을 할 수 없습니다. 따라서 이런 경우에는 줄어든 행렬 F(x)에 맞추기 위해 identity mapping을 한 x에도 후처리를 해줘야합니다. 이를 수식으로 나타내면 다음과 같ㅅ흡니다.
y = F(x,Wi)+Ws*x
위 식에서 Wi는 CNN 레이어에 속한 가중치이고, Ws는 identity mapping을 행렬 덧셈 가능하도록 곱해주는 기능을 한다고 보면 됩니다.


