[선형대수] 특이값 분해(Singular Value Decomposition)의 의미
업데이트:
특이값 분해(Singular Value Decompostion)의 개념과 의미
참고링크
1. 특이값 분해?
안녕하세요. 오늘 다룰 내용은 특이값 분해(Singular Value Decomposition) 입니다. ‘특이값’이라는 단어는 4차 산업혁명을 맞이하여 여러 분야에서 자주 쓰이는데요. ‘특이값’이라는 단어는 분야마다 다른 뜻을 나타내기도 하지만, 딥러닝, 머신러닝, 데이터분석을 하시는 분들은 ‘특이값’ 이라는 단어를 ‘특이값 분해’를 통해 많이 들어보셨을 것 같아요. 하지만 특이값 분해는 자주 쓰이는 것 만큼 이해하는게 간단하지는 않습니다. 자주 활용하시는 분들이라도 그 의미를 모르고 쓰시는 분들도 계시더라구요. 그럼, 특이값 분해란 무엇을 의미하는 것일까요? 오늘 저와 함께 특이값 분해에 대해서 알아보시겠습니다.(조금 어려움 주의)
2. 특이값 분해의 위키백과 정의
선형대수에서, 특이값 분해(Singular Value Decomposition, SVD)란 행렬분해(Matrix Factorization) 방식 중 하나이다. 이 방법은 \(m \times n\) 행렬의 고유값과 고유벡터를 이용한 고유분해(eigen decomposition)의 일반화 된 방식이다.
3. 특이값 분해의 간단한 설명
사실 특이값 분해는 단순하게 생각하면 이전 시간에 다루었던, 고유값 분해의 일반화 버전이라고 생각하시면 편합니다. 여기서 말하는 일반화란, 고유값 분해가 $ m \times m $ 정사각 대칭행렬에서 성립되었다면 특이값 분해는 반드시 정사각행렬일 필요도, 대칭행렬일 필요가 없는 것이죠. 임의의 행렬 $ n \times p $에 대해서도 성립하는 것이 특이값 분해입니다. 즉, 제약이 없어진다는 뜻이죠. 특이값 분해를 이용하면 어떤 종류의 행렬이라도 분해할 수 있습니다. 여기까지만 간단히 알아도 특이값 분해를 사용하시는데 지장은 없으실 겁니다. 만약 특이값 분해에 대해 더 자세히 알고 싶으시면 다음 단락으로 가시겠습니다.
4. 고유값 분해 복습
특이값 분해는 고유값 분해의 일반화 버전이므로, 고유값 분해를 간단히 복습하고 가겠습니다. 모든 대칭행렬 A는 아래와 같이 표현 가능합니다.
$ A = PDP^{T} $
$P$: $A$의 고유벡터로 이루어진 $n \times n$ 직교행렬 $P$
$D$: $A$의 각 고유벡터에 해당하는 고유값을 대각원소로 하는 대각행렬 $D$
고유값 분해를 더 자세히 알고 싶으신 분은 링크를 클릭해주세요.

5. 특이값 분해의 목적
특이값 분해는 행렬을 분해하는 방법 중 하나입니다. 그렇다면 멀쩡한 행렬을 대체 왜 분해하는 것일까요? 이해를 돕기 위해 다른 유명한 분해를 예로 들어보겠습니다. 제가 아는 가장 유명한 분해는 중학교때 배운 인수분해인데요. 인수분해의 목적은 무엇일까요? 인수분해는 이차방정식의 해를 구하기 위한 도구로 쓰이는데요. 이차방정식 자체만 보고 해를 바로 구하는건 꽤 어렵다고 생각합니다. 따라서 수학자들은 인수분해라는 방법을 통해 이차방정식의 해를 좀 더 쉽게 구할 수 있었습니다. 그렇다면 특이값 분해는 어떨까요? 인수분해가 이차방정식의 해를 구하기 위한 도구로 쓰이는 것처럼 특이값 분해도 행렬을 차원축소 하기위한 도구로 쓰입니다. 실제로 주성분분석(PCA, principle component analysis)와 같은 차원축소 분야에서는 특이값 분해가 흔하게 쓰입니다.
6. 특이값 분해의 활용
앞서 특이값 분해는 차원축소를 하는데 사용된다고 말씀드렸는데, 좀 더 구체적으로 알아보겠습니다. 데이터를 나타내는 행렬 A가 존재한다고 합시다. 차원축소는 말그대로 차원을 축소시키는 것인데요, 즉, 데이터 전체 공간의 차원보다 낮은 차원으로 근사시켜 적합(fit)시킬 수 있는 차원이 낮은 공간을 찾는 것입니다. 만약 A가 d차원이라고 했을때, A를 k차원(d>k)으로 축소시킨 행렬을 B라고 하면 결국 특이값 분해는 차원축소 행렬 B를 찾는 데 사용되는 것입니다. 이 때, 저희가 k를 정할 수 있는데요, 말그대로 1차원으로 줄일수도 있고, 2차원으로 줄일 수도 있는 것이죠. 아래 그림은 3차원공간의 데이터들을 2차원 공간으로 적합시킨 예 입니다.
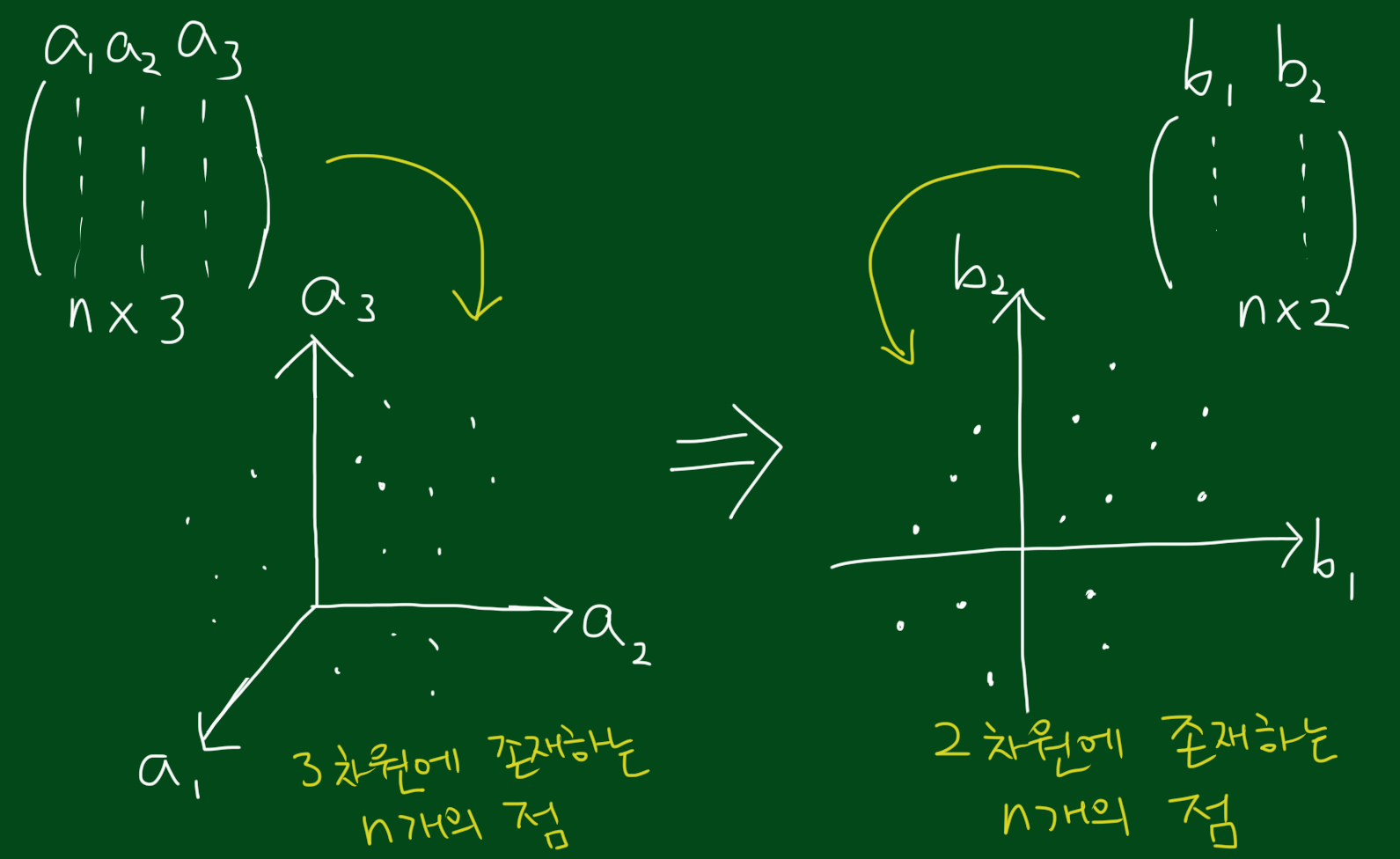
7. 특이값 분해의 기준행렬
행렬 A의 크기가 $n \times d$이라는 말은 d차원에서 n개의 점이 있다고 생각하실 수 있습니다. 따라서 A에 대한 차원축소란 n개의 점을 표현할 수 있는 p보다 작은 차원인 d차원-부분공간을 찾는 문제라고 볼 수 있습니다. 그렇다면 해당 부분공간은 어떻게 구할까요? 그것은 데이터와 부분 공간으로부터의 수직거리를 최소화 시키는 것이라고 볼 수 있습니다. 이때 직선거리의 최소화는 회귀분석에 나오는 제곱합(sum of squre)를 최소화 시키는 것이죠. 제곱합이라고 했으니 $ A^{T}A, AA^{T}$ 를 사용하는 것이고, 따라서 특이값 분해에서는 원본행렬 A 자체를 다루기보다는 $ A^{T}A, AA^{T}$ 를 다루는 것입니다.
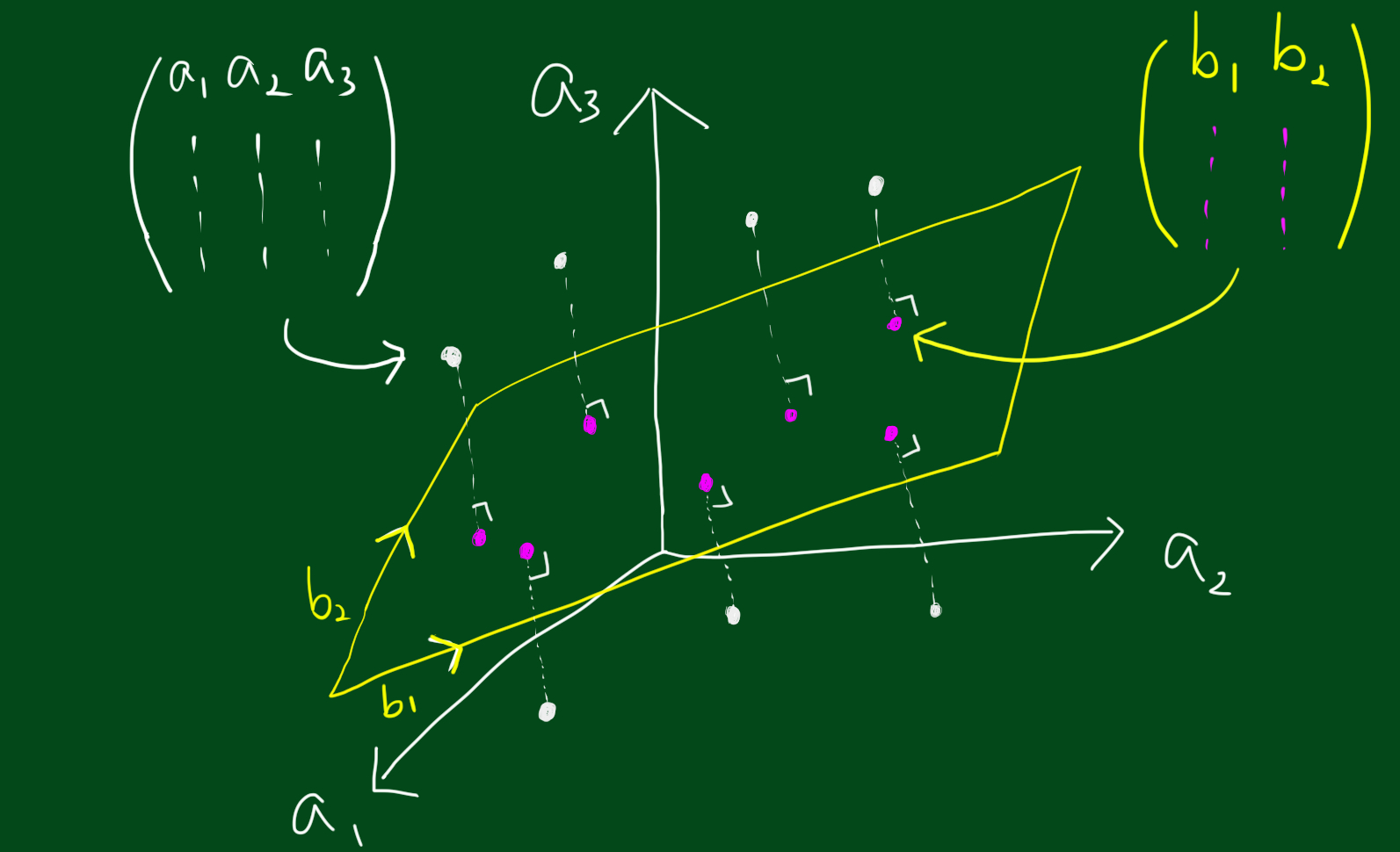
또한 $AA^{T}$는 A의 행의 내적이라고 볼 수 있고 이는 A의 행과 원점과의 거리를 나타내는 것입니다. 또한 $A^{T}A$는 A의 열의 내적이라고 볼 수 있고 이는 A의 열과 원점과의 거리라고 볼 수 있습니다. 아래 그림을 참고해주시고, 내적에 대해서 복습하고 싶으신 분은 링크를 클릭해주세요.
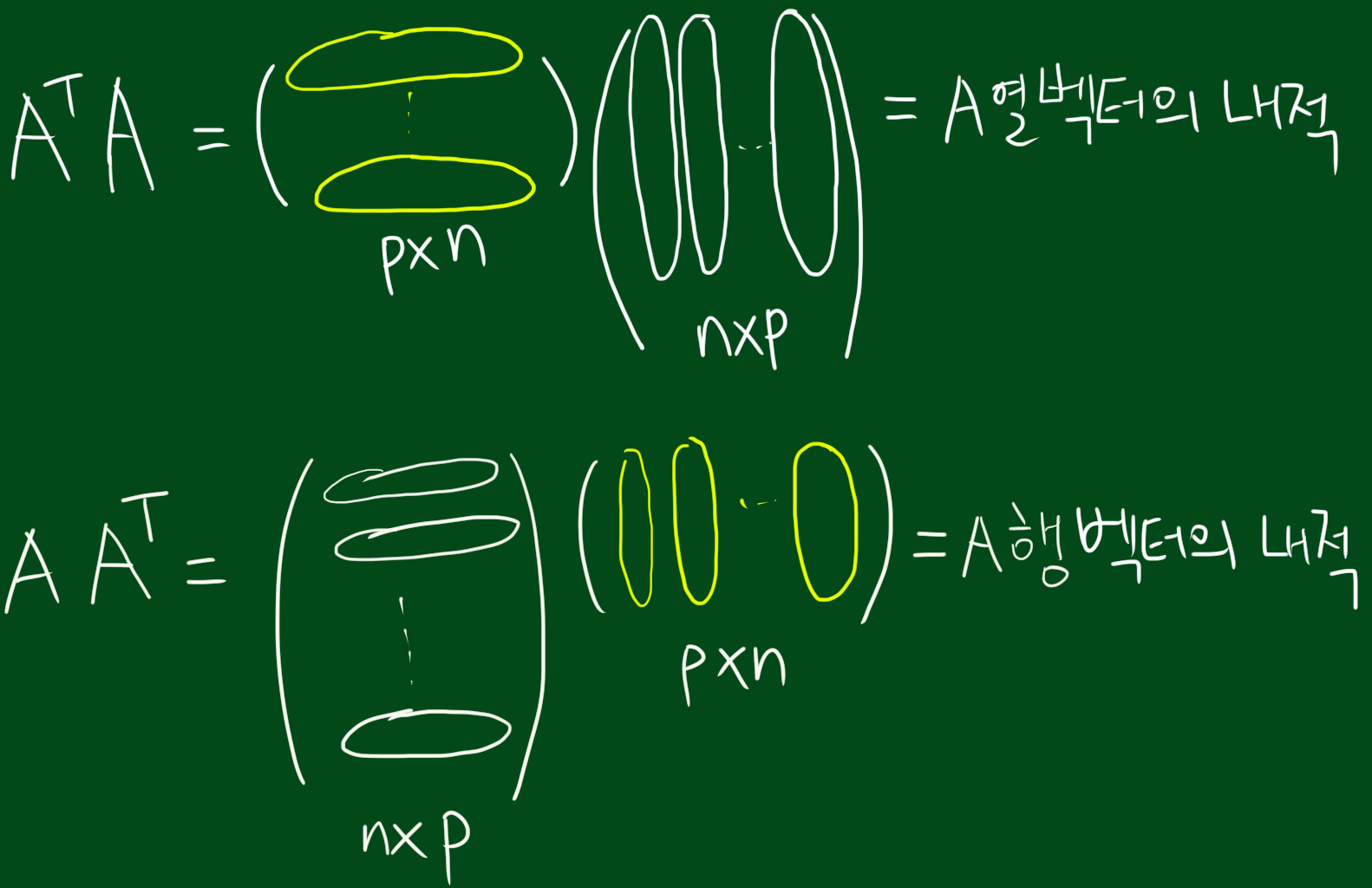
8. 특이값이란 무엇인가, 특이값의 정의
자 그럼 이제 특이값 분해에서 말하는 ‘특이값’이라는 단어의 뜻을 알아보겠습니다. 특이값의 정의는 아래와 같습니다.
$ n \times p $ 행렬 A에 대해 $ A^{T}A $의 고유값을 $ \lambda_{1}, …, \lambda_{p} $ 라고 할 때, $ \sigma_{1} = \sqrt{\lambda_{1}}, \sigma_{2} = \sqrt{\lambda_{2}}, … ,\sigma_{p} = \sqrt{\lambda_{p}}$ 를 A의 특이값(sigular value)라고 합니다.
간단히 설명드리면 A를 제곱한 행렬의 고유값이니 루트(root)를 씌운다고 생각하시면 될 것 같습니다. 비유가 정확한지는 모르겠으나, 분산과 표준편차의 관계라고 생각하면 조금 이해가 되실지 모르겠습니다.
9. 특이값 분해란?
자 그러면 특이값 분해란 무엇일까요. 특이값 분해는 고유값 분해의 일반화 버전이라고 말씀드렸듯이, 분해의 전체적인 형태는 고유값 분해와 같습니다.
고유값분해는 $A = PDP^{T} $의 형태로 나타냈지만, 특이값분해는 $A = U \sum V^{T}$로 나타냅니다. 이 때, U 는 $AA^{T}$의 고유벡터를 열로 구성 하고 left singular vector라고 부르고, V 는 $A^{T}A$의 고유벡터를 열로 구성하고 right sigular vector라고 부릅니다. 또한 $\sum $ 의 각 대각원소는 행렬 A의 특이값입니다.
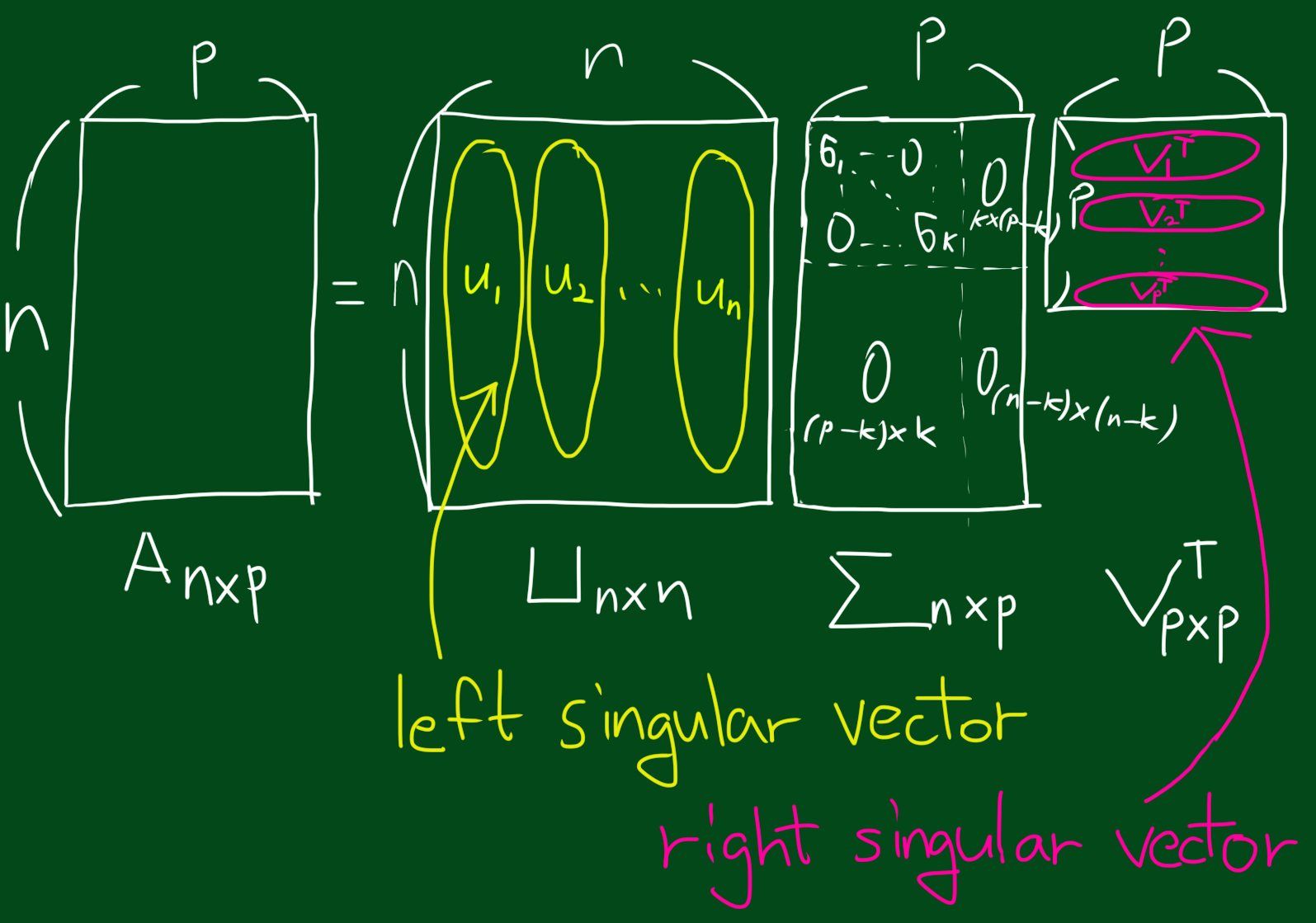
11. 정리
고유값 분해는 대칭행렬 A에 대해 A를 고유값, 고유벡터를 이용해 분해하는 것이었는데요. 이를 일반화 시킨 특이값 분해는 임의의 행렬 A에 대해 $A^{T}A, AA^{T}$의 고유값, 고유벡터를 이용해 분해하는 것 입니다. 끝으로 위키백과 정의를 다시 한 번 보고 오늘 포스팅을 마치겠습니다.
선형대수에서, 특이값 분해(Singular Value Decomposition, SVD)란 행렬 분해(matrix factorizaition) 방식 중하나이다. 이 방법은 $m \times n$ 행렬의 고유값과 고유벡터를 이용한 고유분해(eigendecomposition)의 일반화된 방식이다.


