[기초통계] 감마분포 의미 및 개념 정리
업데이트:
감마분포 의미 및 개념 정리
참고링크
- 확률변수 복습하기
- 확률분포 복습하기
- 모집단과 표본 복습하기
- 평균과 분산 복습하기
- 공분산, 상관계수 복습하기
- 최대가능도추정 복습하기
이산확률분포
- 베르누이분포, 이항분포
- 기하분포, 음이항분포
- 초기하분포
- 포아송분포
연속확률분포
- 정규분포
- 감마분포
- 지수분포
- 카이제곱분포
- 베타분포
- 균일분포
1. 감마분포의 정의
감마분포는 연속확률분포로, 두개의 매개변수를 받으며 양의 실수를 가질 수 있다.
위 정의는 위키백과에서 가지고 온 것인데요. 자세하게 나와있지는 않아서 보충설명해 드리면, 감마분포는 $\alpha$번째 사건이 발생할때까지의 대기시간의 분포라고 생각하시면 될 것 같습니다.
2. 감마함수의 정의
감마분포를 이야기하기 전에 감마함수를 먼저 아셔야하는데요. 감마함수를 알아보도록 하겠습니다. 감마합수는 아래와 같은데요. 뭔가 복잡해보이지만 하나의 표현식이라고 생각하시면 편하실 것 같습니다.
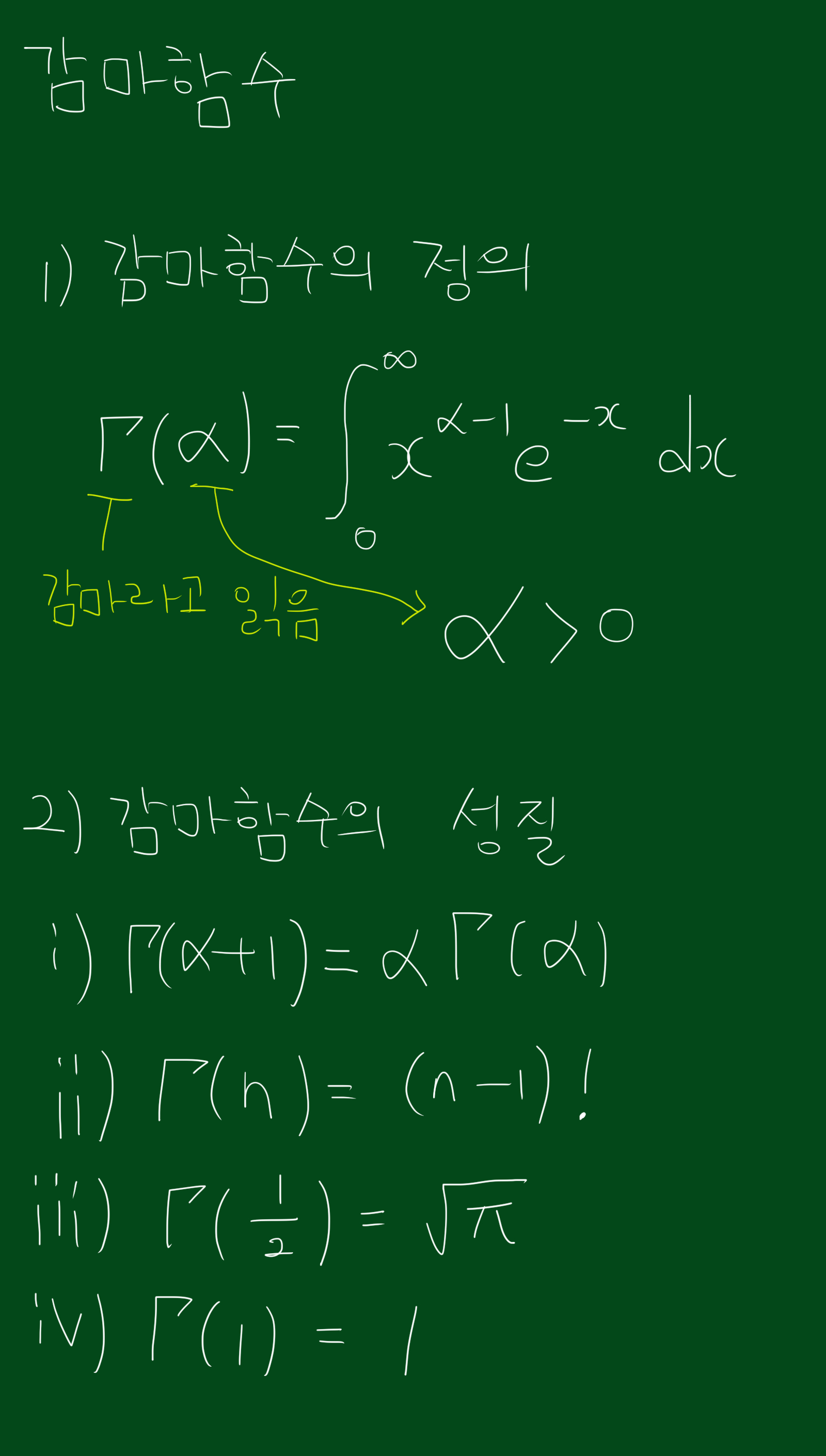
3. 감마분포의 확률밀도함수, 평균, 분산
감마분포의 확률밀도함수, 평균, 분산은 다음과 같습니다.
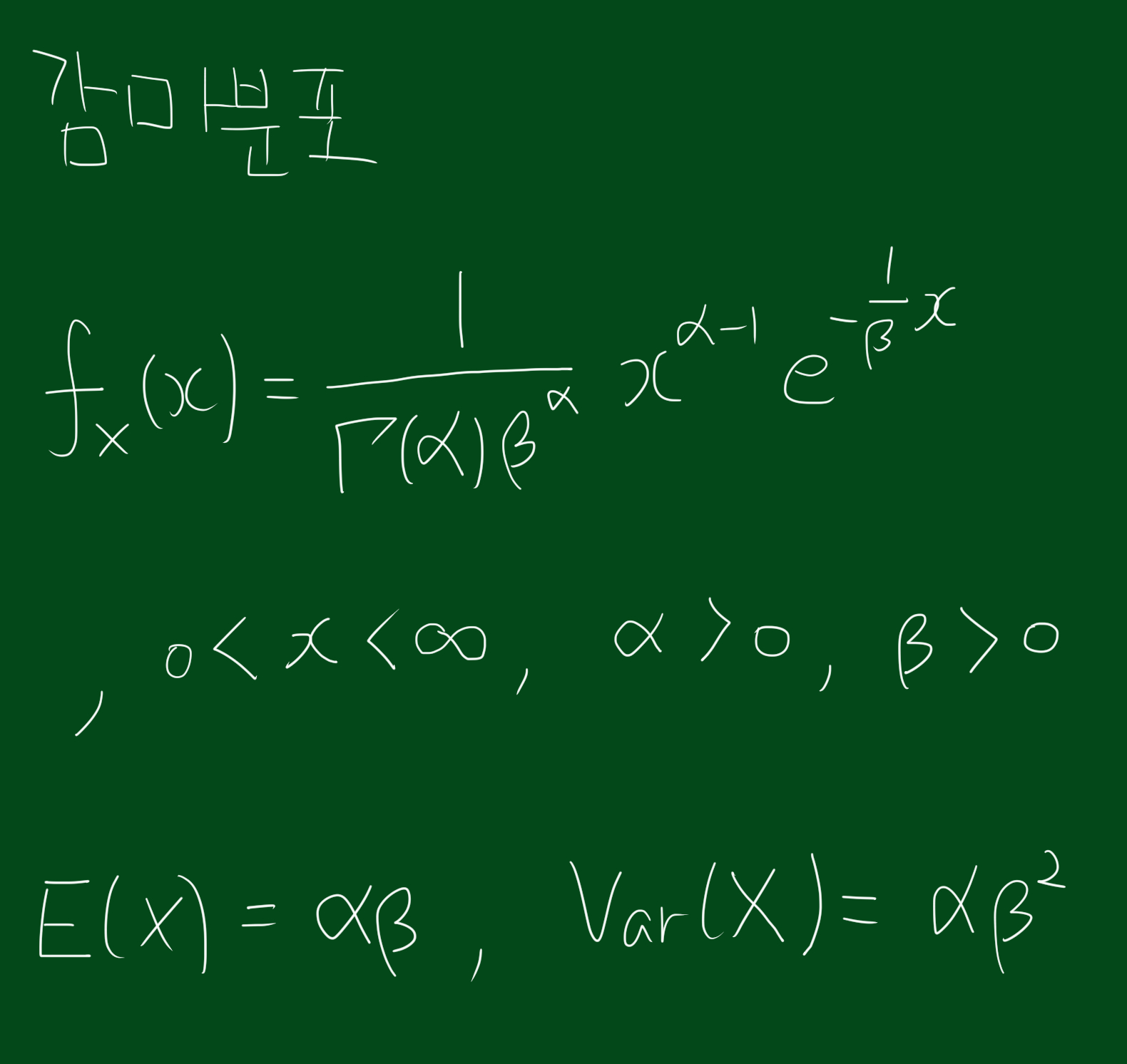
4. 감마분포 vs 지수분포
감마분포는 지수분포와 관련이 있는데요. 지수분포는 첫번째 사건이 발생할 때 까지의 대기시간의 분포인 반면, 감마분포는 $\alpha$번째 사건이 발생할 때 까지의 대기사간의 분포라고 보시면 됩니다. 즉, 지수분포는 감마분포의 특수한 경우라고 생각하시면 되겠습니다.
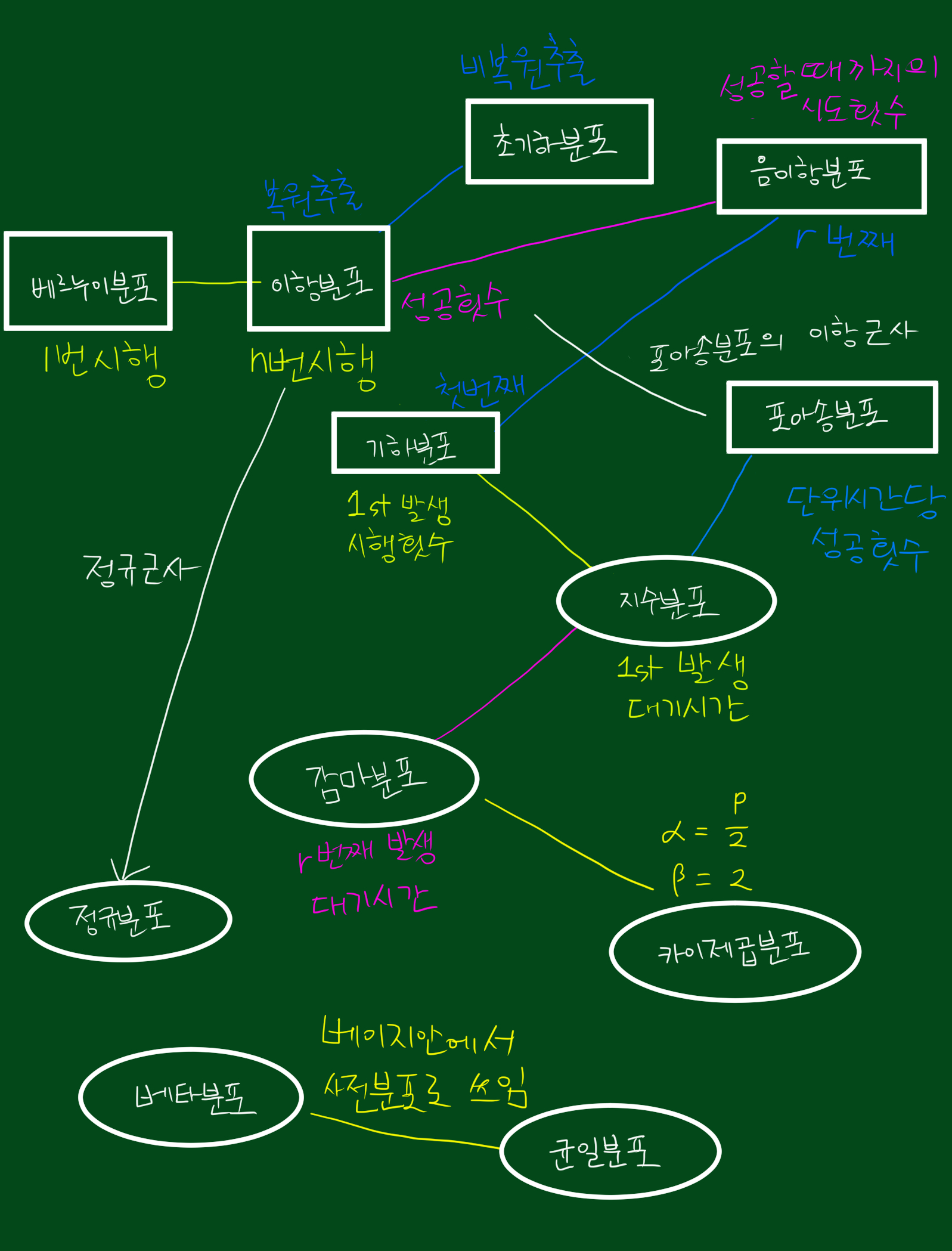
참고. 확률분포간 관계도
