[기초통계] 베타분포 의미 및 개념 정리

베타분포 의미 및 개념 정리

참고링크

머신러닝	딥러닝	선형대수	기초통계	최적화
k-means	신경망이란	고유값,고유벡터	확률변수	컨벡스 셋
k-최근접이웃	성능함수	행렬식	확률분포	컨벡스 함수
선형회귀	신경망 학습	내적	모집단과 표본	라그랑주 듀얼
로지스틱회귀	교차연결	기저	평균과 분산	KKT 조건
릿지,라쏘회귀	합성곱 신경망	랭크, 차원	공분산, 상관계수	ROC 커브
의사결정나무	배치, 에포크 차이	선형변환	최대가능도추정	크로스 밸리데이션
서포트벡터머신	텐서플로기초(1)	직교행렬	베르누이,이항분포	실루엣 스코어
원클래스 SVM	텐서플로기초(2)	고유값분해	기하,음이항분포
LDA	seq2seq	특이값분해	초기하분포
GMM	opencv기초		포아송분포
부스팅	resnet		정규분포
사이킷런 실습	다각형내부판별		감마분포
	엣지판별		지수분포
			카이제곱분포
			베타분포
			균일분포

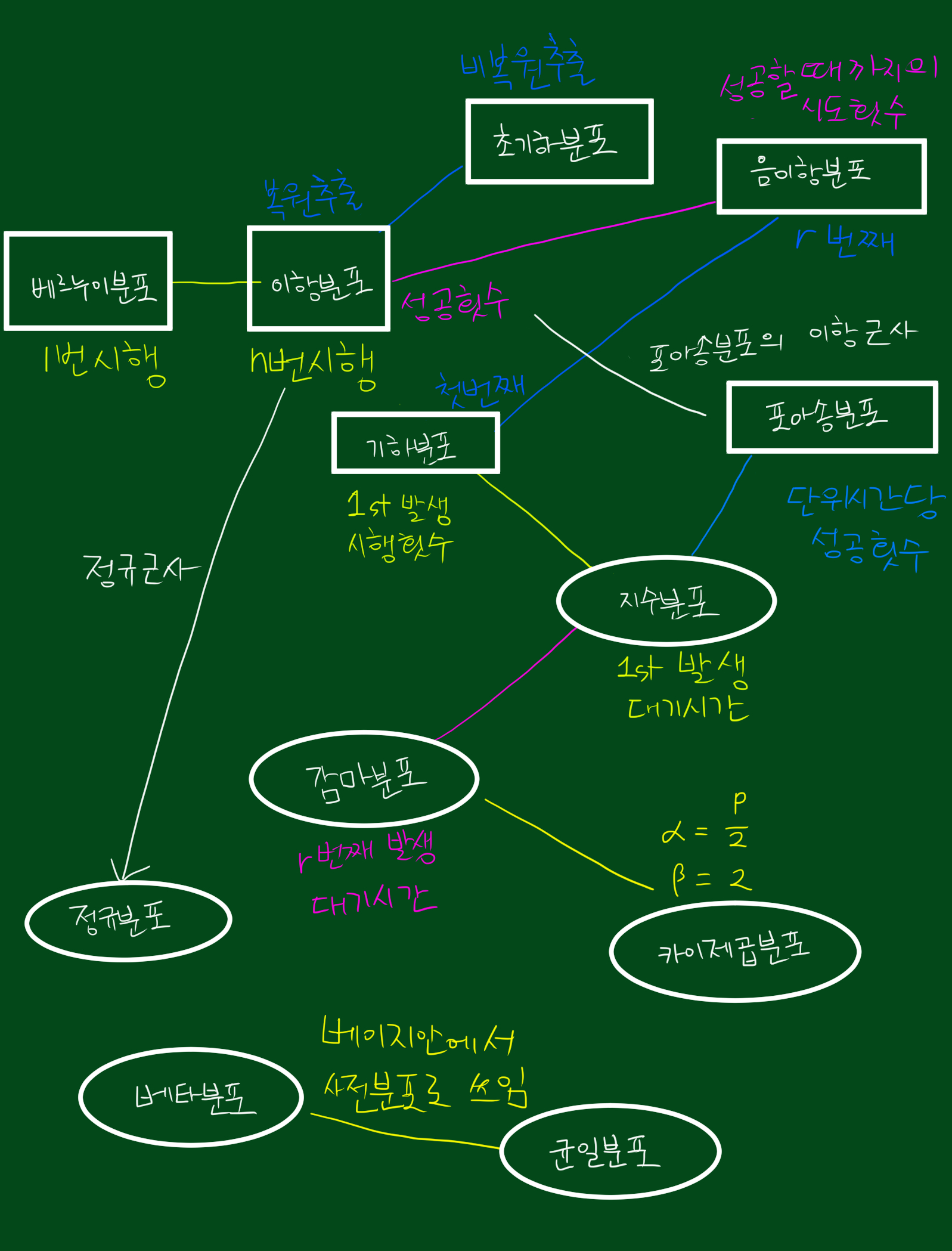
1. 베타분포의 정의

베타분포(beta distribution)는 두 매개변수 $\alpha$와 $\beta$에 따라 [0, 1] 구간에서 정의 되는 연속확률분포이다.

위 정의에서 매개변수란 분포의 형태를 결정짓는 모수라고 생각하시면 되겠습니다. 또한 같은 0과 1사이에서 정의 되는 부분은 균일분포와 비슷한 연속확률분포라고 할 수 있겠습니다.

2. 베타분포의 쓰임새

흔히 베이지안에서 사후확률을 가정할때 베타분포를 가정하곤 합니다. 왜냐하면 모수에 따라 다양한 형태로 변형 가능하기 때문입니다.

3. 베타함수 정의

베타분포를 알기 위해서는 베타함수를 먼저 아시는 것이 좋습니다. 참고로 베타함수를 알기 전에 감마함수를 먼저 아시는 것이 좋은데요. 감마함수에 대해서는 링크 참고 부탁드립니다. 베타함수는 아래와 같이 정의 됩니다.

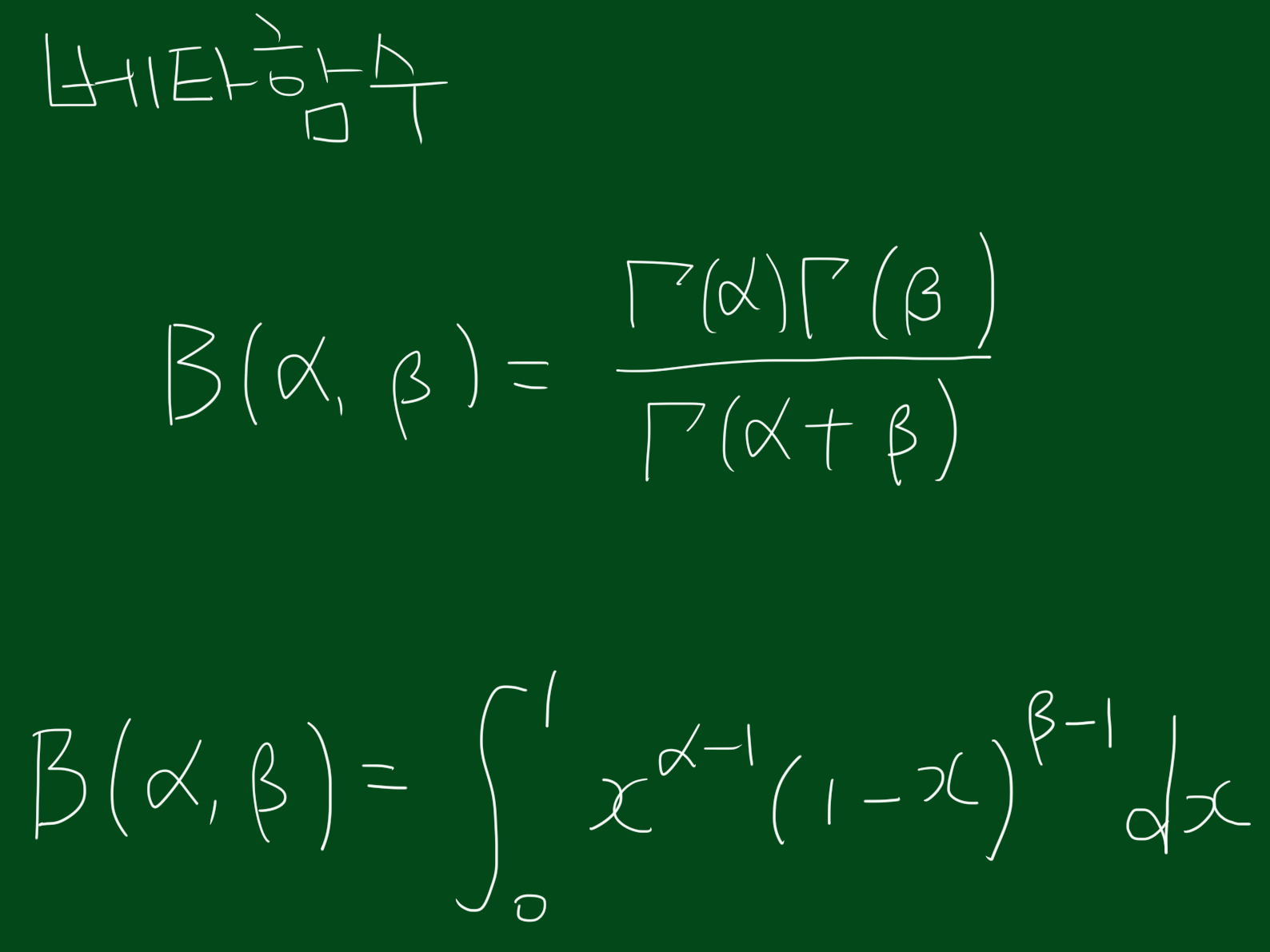
4. 베타분포의 확률밀도함수, 평균, 분산

베타분포의 확률밀도함수, 평균, 분산은 다음과 같습니다.

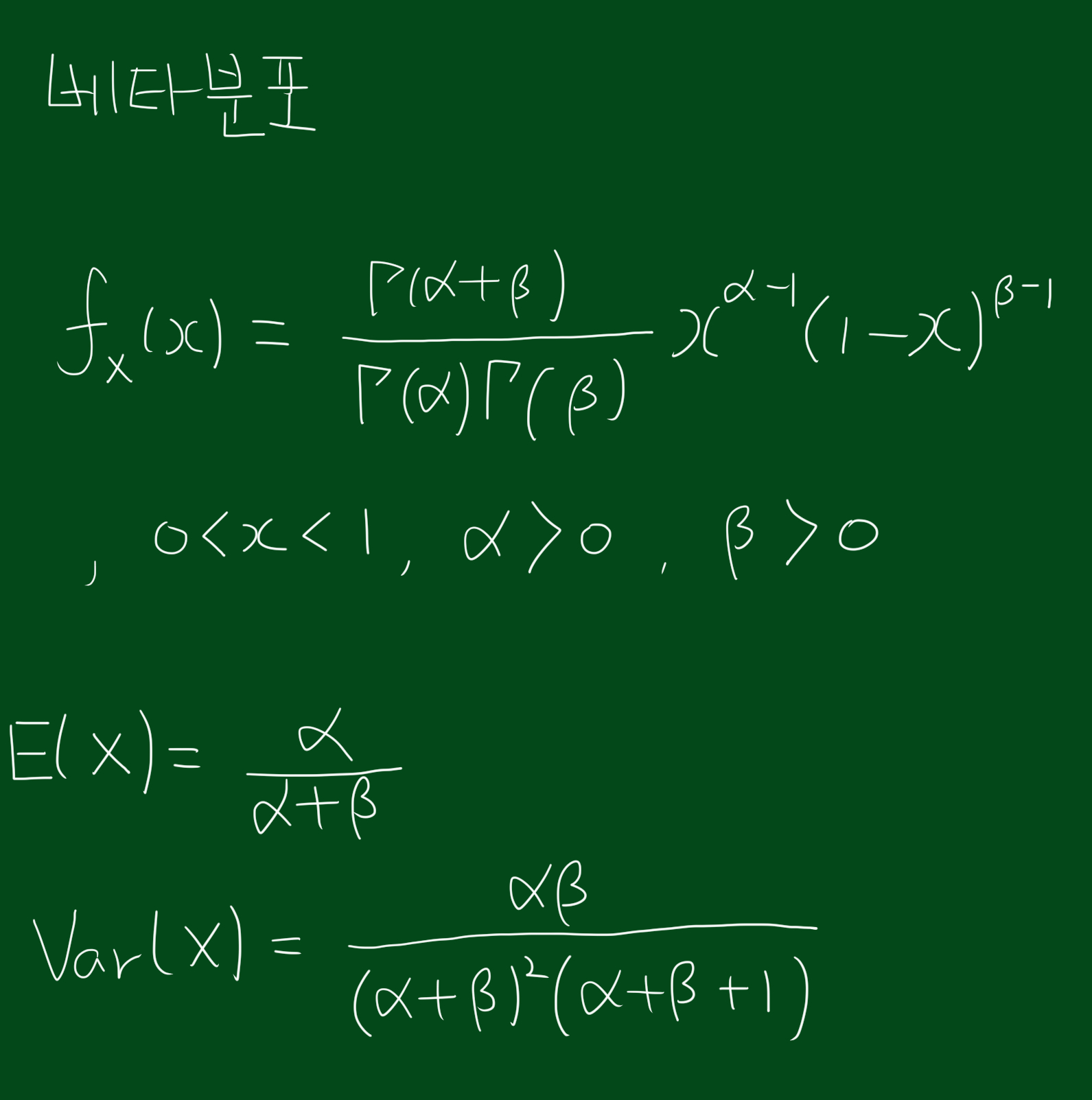
참고. 확률분포간 관계도