[선형대수] 랭크(rank), 차원(dimension)의 의미

랭크(rank), 차원(dimension)의 의미

참고링크

머신러닝	딥러닝	선형대수	기초통계	최적화
k-means	신경망이란	고유값,고유벡터	확률변수	컨벡스 셋
k-최근접이웃	성능함수	행렬식	확률분포	컨벡스 함수
선형회귀	신경망 학습	내적	모집단과 표본	라그랑주 듀얼
로지스틱회귀	교차연결	기저	평균과 분산	KKT 조건
릿지,라쏘회귀	합성곱 신경망	랭크, 차원	공분산, 상관계수	ROC 커브
의사결정나무	배치, 에포크 차이	선형변환	최대가능도추정	크로스 밸리데이션
서포트벡터머신	텐서플로기초(1)	직교행렬	베르누이,이항분포	실루엣 스코어
원클래스 SVM	텐서플로기초(2)	고유값분해	기하,음이항분포
LDA	seq2seq	특이값분해	초기하분포
GMM	opencv기초		포아송분포
부스팅	resnet		정규분포
사이킷런 실습	다각형내부판별		감마분포
	엣지판별		지수분포
			카이제곱분포
			베타분포
			균일분포

안녕하세요, 오늘은 선형대수에서 아주 중요한 개념인 랭크(Rank)와 차원(Dimension)에 대해 알아보겠습니다. 그 전에 우선 벡터공간, 부분공간의 설명이 선행되어야 하므로 벡터공간에 대한 설명으로 시작하겠습니다.

벡터공간(Vector Spaces)

지난 시간에 설명드렸던 기저(basis)에서 알 수 있듯, 기저는 벡터 공간을 생성하는 선형독립인 벡터들이라고 했습니다. 반대로 말하면 벡터공간은 기저 벡터로 생성 가능한 공간 이라고 생각할 수 있겠네요. 좀 더 간단히 말하면 어떤 벡터 집합이 있을때, 그 벡터들로 구성할 수 있는 공간을 벡터 공간이라고 하면 이해하기 쉬우실 것 같아요. 혹시 지금까지 설명이 어려우시다면 기저(basis)를 참고해주세요.

부분공간(Subspaces)

부분공간은 이름 그대로 전체 공간의 일부분을 의미합니다. 즉, 어떤 벡터집합의 일부분으로 만든 공간을 전체 공간의 부분 공간이라고 합니다. 예를들어 기저벡터 3개가 있다고 하면, 그 3개의 벡터로 만들수 있는 공간을 전체 벡터공간이라고 하며, 기저벡터 3개 중 일부인 2개나 1개만 사용해서 만들수 있는 공간이 부분공간입니다. 예를 들어, 전체 공간을 3차원 공간이라 했을때 전체 공간의 일부인 선(line)이나 면(plane)은 3차원 공간의 부분공간이라고 할 수 있죠.

Span

편의상 전체 벡터공간 V가 10차원이고, 2개의 기저 벡터 집합을 S라고 하고, 집합 S에 속하는 기저 벡터들로 구성되는 2차원 부분 공간을 W라고 했을 때 S는 부분 공간 W를 span한다고 말하고 W = span(S) 라고 표현합니다. 위의 예에서는 전체가 10차원 공간이지만 기저벡터가 2차원까지만 표현 가능하므로, span되는 공간은 2차원이라고 할 수 있죠. span은 자주 쓰이기도 하고 중요한 개념이므로 확실히 알아두시면 좋습니다.

열공간(column spaces), 행공간(row spaces)

행렬을 바라보는 방식에는 두 가지가 있습니다.

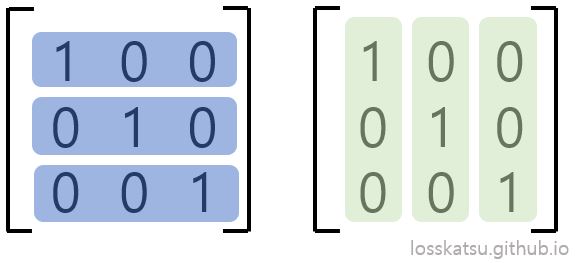
전자와 같이 행기준으로 표현했을때는 행렬의 행벡터라고 부르고, 후자와 같이 표현했을때는 열벡터라고 부릅니다. 마찬가지로 벡터가 주어졌을때, 그들로 행렬을 구성하는 방식에도 두가지가 있습니다.

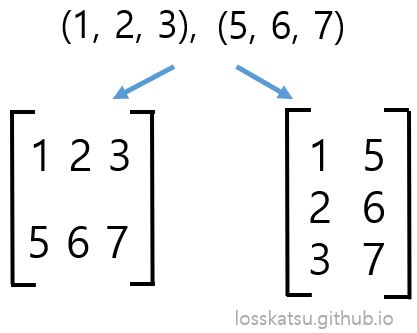
벡터공간의 정의를 응용하면 행벡터로 span 할 수 있는 공간을 행공간이라고 부르고, 열벡터로 span 할 수 있는 공간을 열공간이라고 부릅니다. 다른 말로는 어떤 행렬의 행(열)벡터들이 나타낼 수 있는 선형결합의 집합이라고 할 수 있습니다.

영공간(null spaces)

영공간은 Ax = 0 을 만족시키는 벡터 x의 모임을 뜻합니다. 앞서 내적의 정의를 연관지어 생각하면, x를 기저벡터라고 놓고 Ax를 행렬 A를 기저 x에 정사영 시킨다고 생각해 봅시다. 그러면 Ax=0이라고 했으니 A와 x의 내적의 결과가 영벡터라는 것을 알 수 있습니다. 이해가 잘 안되신다면 아무 것도 없는 공간이라고 생각하실 수 있을 거같아요. 정리하면 주어진 행렬 A가 있을때 행렬 A는 열공간, 행공간, 영공간으로 구성 됩니다.

차원(dimension)

차원을 설명하기 위해선 기저(basis)에 대한 이해가 선행 되어야 하는데요. 기저 포스팅에서 알 수 있듯, 기저는 한 공간을 구성 할 수 있는 벡터 집합입니다. 그리고 기저 벡터의 갯수를 차원(dimension)이라고 부르는데요. 쉽게 말해서 3차원 공간을 구성하는데는 3개의 기저벡터가 필요하다는 뜻이지요. 그럼 10차원 공간을 구성하는데는 몇개의 기저벡터가 필요할까요? 네, 10개가 필요합니다. 참고로 영공간의 차원은 nullity라고 부릅니다.

열공간과 행공간의 차원

그렇다면 열공간의 차원과 행공간의 차원은 같을까요, 다를까요? 직관적으로 생각해본다면, 행공간이나 열공간이나 결국 같은 행렬을 바라보는 관점의 차이일 뿐이므로 행공간의 차원과 열공간의 차원은 같습니다.

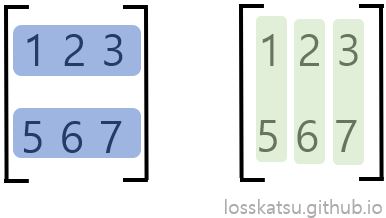
위 행렬을 전자와 같이 보았을땐 행렬 2개로 만드는 공간이라고 볼 수 있죠. 반면 후자와 같이 바라본다면 행렬 3개로 만드는 공간이라고 볼 수 있습니다. 이런 경우 행공간의 차원과 열공간의 차원을 무엇일까요? 얼핏 보면 행공간은 벡터 2개이니 2차원, 열공간은 벡터 3개이니 3차원이라고 생각할 수 있지만, 열공간의 차원 사실 2입니다. 벡터는 3개이지만 3개 모두 선형 독립은 아니거든요. 기저 <- 참고

랭크(Rank)

자, 드디어 랭크까지 왔습니다. 위에서 여러가지 설명을 했던건 다 지금부터 설명할 랭크를 설명하기 위함이었습니다. 아마 지금까지 잘 따라오셨다면 랭크도 이해하실 수 있을 것입니다.
사실 이 부분은 수식없이 설명하기 좀 어려운 부분이 있지만…음…우선 위키백과 정의부터 보겠습니다.

In linear algebra, the rank of a matrix A is the dimension of the vector space generated (or spanned) by its columns.

위키백과 정의에 의하면 어떤 행렬 A의 랭크는 해당 행렬의 열벡터에 의해 span된 벡터공간의 차원 이라고 합니다.

따라서 위 행렬의 랭크는 2 입니다.

랭크의 성질

앞에서 행공간과 열공간의 차원은 같다고 했죠. 이와 연관된 랭크의 중요한 성질 중 하나는 아래와 같습니다.

$ rank(A) = rank(A^{T}) $

즉, 어떤 행렬 A의 랭크와 A의 전치행렬의 랭크는 같다는 것입니다. 또한 A가 m by n 행렬이라고 했을 때, 앞서 말한 차원을 랭크의 개념을 이용해서 설명하면 아래와 같이 표현할 수 있습니다.

$ n = rank(A) + nullity(A) $

$ m = rank(A^{T}) + nullity(A^{T}) $

여기서 n은 열수, m은 행수를 의미합니다. 또한, $n = rank(A)$, 혹은 $m = rank(A^{T})$일때 풀 랭크(full rank)라고 합니다.