[기초통계] 지수분포 의미 및 개념 정리

지수분포 의미 및 개념 정리

참고링크

머신러닝	딥러닝	선형대수	기초통계	최적화
k-means	신경망이란	고유값,고유벡터	확률변수	컨벡스 셋
k-최근접이웃	성능함수	행렬식	확률분포	컨벡스 함수
선형회귀	신경망 학습	내적	모집단과 표본	라그랑주 듀얼
로지스틱회귀	교차연결	기저	평균과 분산	KKT 조건
릿지,라쏘회귀	합성곱 신경망	랭크, 차원	공분산, 상관계수	ROC 커브
의사결정나무	배치, 에포크 차이	선형변환	최대가능도추정	크로스 밸리데이션
서포트벡터머신	텐서플로기초(1)	직교행렬	베르누이,이항분포	실루엣 스코어
원클래스 SVM	텐서플로기초(2)	고유값분해	기하,음이항분포
LDA	seq2seq	특이값분해	초기하분포
GMM	opencv기초		포아송분포
부스팅	resnet		정규분포
사이킷런 실습	다각형내부판별		감마분포
	엣지판별		지수분포
			카이제곱분포
			베타분포
			균일분포

1. 지수분포의 정의

지수분포(exponential distribution)은 연속확률분포의 일정이다. 사건이 서로 독립적일 때, 일정 시간 동안 발생하는 사건의 횟수가 포아송분포를 따른다면, 다음 사건이 일어날 때까지의 대기 시간은 지수분포를 따른다. 이는 기하분포와 유사한 측면이 있다.

2. 지수분포의 확률밀도함수, 평균, 분산

지수분포의 확률밀도함수, 평균, 분산은 아래와 같습니다.

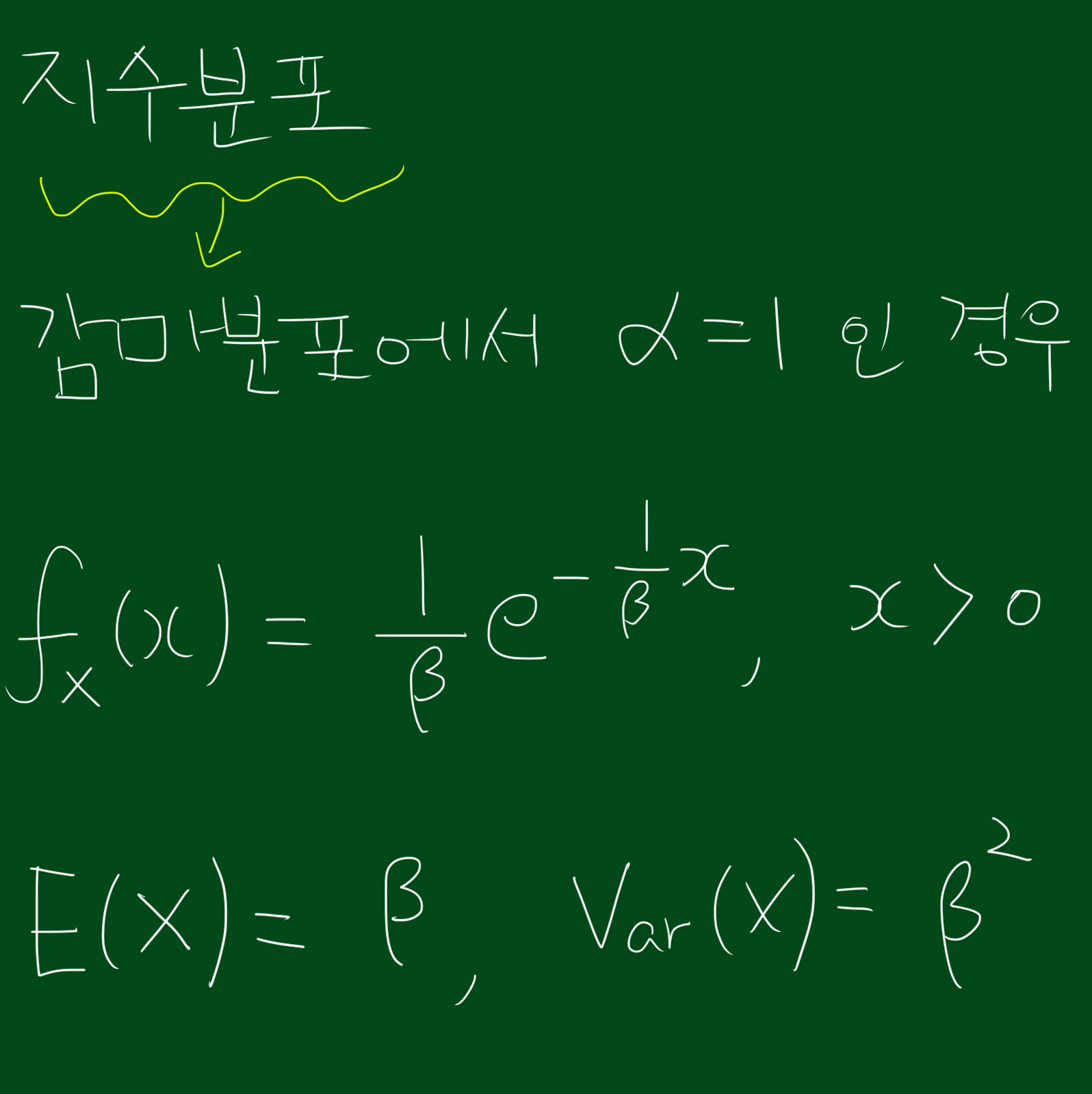
3. 지수분포 vs 포아송분포

지수분포의 정의에서도 언급되었듯이 지수분포는 여러가지 분포와 연관지어 생각할 수 있습니다. 먼저 알아볼 것은 포아송분포와의 관계인데요. 포아송분포와 지수분포는 사건을 바라보는 관점이 다릅니다. 어떤 단위 시간 동안 발생하는 사건을 관찰한다고 했을때, 포아송분포는 단위 시간 당 발생하는 사건의 횟수를 관측합니다. 반면 지수분포는 사건이 일어날때까지의 대기 시간을 관측합니다. 즉, 지수분포는 대기시간, 포아송분포는 횟수 입니다.

4. 지수분포 vs 기하분포

지수분포는 또한 기하분포와도 관련이 있는데요. 지수분포는 사건이 발생할때가지의 대기시간 인 반면, 기하분포는 사건이 발생할때까지의 시도횟수 입니다. 이러한 차이는 결국 지수분포는 연속형 확률분포이고 기하분포는 이산형 확률분포라는 것을 알 수 있습니다.

5. 지수분포 vs 감마분포

지수분포는 감마분포의 특별한 형태입니다. 2.에서 지수분포의 확률밀도함수를 보시면 지수분포는 감마분포에서 $\alpha$가 1인 경우라는 것을 알 수 있습니다.

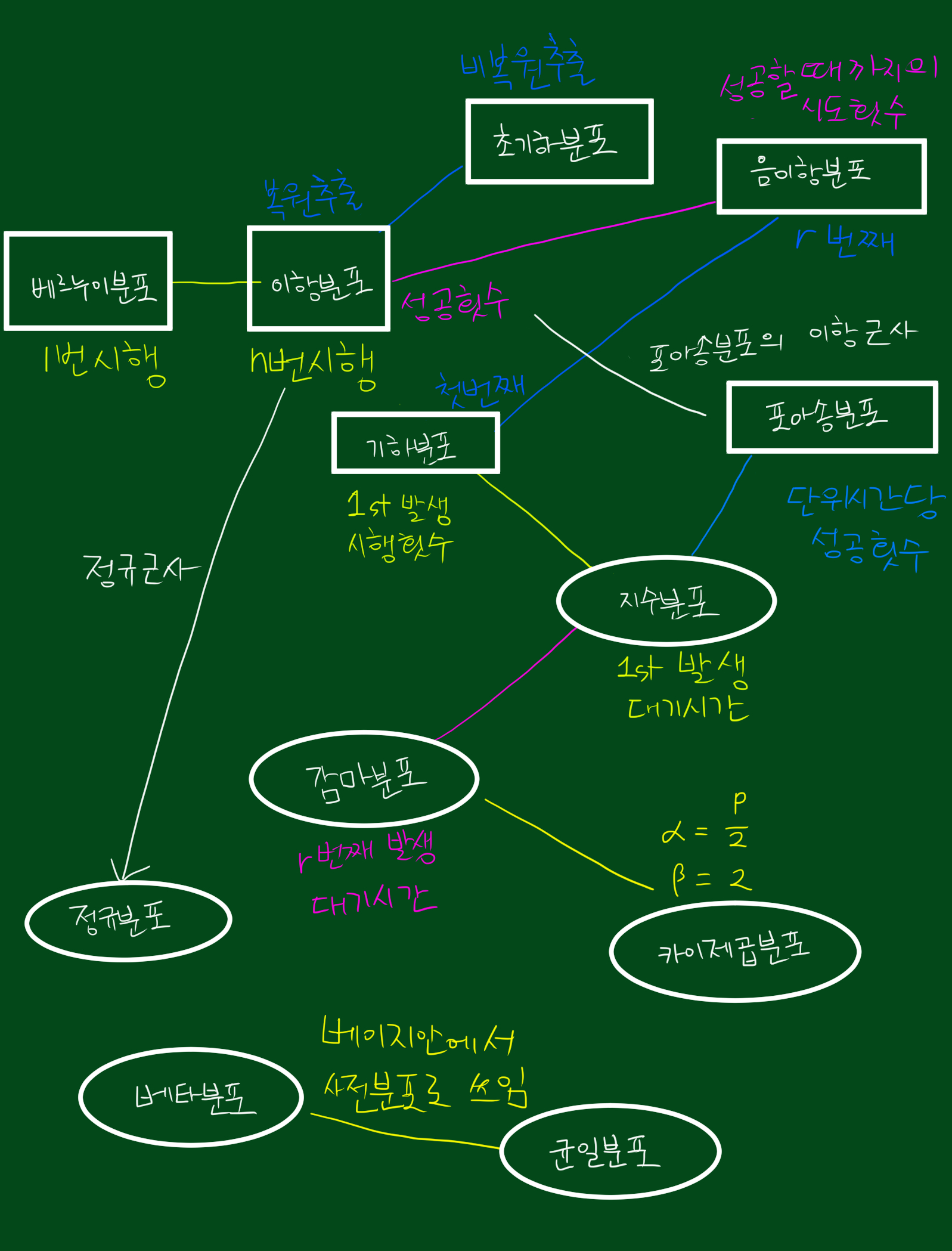
참고. 확률분포간 관계도