[선형대수] 내적(inner product) 의미
업데이트:
내적(inner product)의 의미
참고링크
내적은 여러가지 연산 중 하나 입니다.
우리가 흔히 생각할 수 있는 연산이라고 하면 더하기, 빼기, 곱하기, 나누기 정도가 있는데,
내적도 이러한 연산 중 하나라고 생각하시면 편합니다.
특이한 점은 내적은 벡터와 벡터의 연산인데 결과가 스칼라라는 점입니다.
대개의 경우, ‘벡터+벡터=벡터’, ‘스칼라+스칼라=스칼라’와 같은 형태처럼 인풋과 아웃풋의 형태가 같지만,
이 내적이라는 연산은 신기하게도 벡터와 벡터를 연산 하는데 스칼라라는 아웃풋이 나옵니다.
그럼 내적은 어떤 연산이고 어떤 의미가 있을까요?
1.내적의 정의
앞서 내적은 연산이라고 말씀드렸습니다. 그럼 간단히 내적이 어떤 연산인지 확인해 봅시다.
$ \langle \mathbf{u}, \mathbf{v} \rangle = \mathbf{u} \cdot \mathbf{v} = u_{1}v_{1} + u_{2}v_{2} + \dots + u_{n}v_{n} $
위와 같은 연산을 쉽게 생각하면 벡터의 element들끼리 곱한 후 더한다라고 생각할 수도 있지만, 벡터곱으로 생각할 수 있습니다. 예를 들어 $\mathbf{u}, \mathbf{v}$를 아래와 같이 열벡터의 형태라고 생각해봅시다.
$ \mathbf{u} =
\begin{pmatrix}
u_{1}
u_{2}
\vdots
u_{n}
\end{pmatrix}
, \mathbf{v} =
\begin{pmatrix}
v_{1}
v_{2}
\vdots
v_{n}
\end{pmatrix} $
위와 같은 두 열벡터의 내적은 아래와 같이 표현할 수 있습니다.
$ \mathbf{u} \cdot \mathbf{v} = \mathbf{u}^{T}\mathbf{v} $
즉, 두 열 벡터의 내적을 구하려고 할 경우 둘 중 하나의 벡터를 transpose 시켜 행 벡터의 형태로 바꾼 후, 나머지 벡터와 벡터곱을 시키는 것입니다..
이 내적이라는 연산을 사용하면, 우리가 흔히 알고있는 한 벡터의 norm을 구한다던가, 두 벡터 사이의 거리를 측정하는데 이용할 수 있습니다.
벡터 $\mathbf{v}$의 norm, norm은 벡터의 길이(length)라고도 표현합니다. 그리고 norm이 1인 벡터는 unit vector라고 부릅니다.
$ \parallel \mathbf{v} \parallel = \sqrt{\langle \mathbf{v}, \mathbf{v} \rangle} $
벡터 $\mathbf{u}$, $\mathbf{v}$ 사이의 거리
$ d(\mathbf{u}, \mathbf{v}) = \parallel \mathbf{\mathbf{u} - \mathbf{v}} \parallel = \sqrt{\langle \mathbf{u} - \mathbf{v}, \mathbf{u} - \mathbf{v} \rangle} $
즉, 우리가 알고 있는 norm, distance 의 개념은 내적을 이용해서 표현 가능합니다.
2.내적의 성질
위와 같은 내적의 정의를 이용하면 아래와 같은 성질을 생각할 수 있습니다.
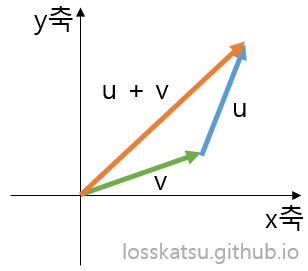
$ \parallel \mathbf{u} + \mathbf{v} \parallel \leq \parallel \mathbf{u} \parallel + \parallel \mathbf{v} \parallel $
즉 어떤 두 벡터의 합의 길이는 각각의 길이의 합보다 작거나 같다는 뜻이며, 아래와 같이 그림으로 생각하면 좀 더 이해하기 편합니다.
3.물리학 관점으로 보는 내적
내적은 기하학 관점 뿐 만 아니라, 물리학 관점으로도 볼 수 있습니다. 먼저 원점으로부터 시작되는 두 벡터가 존재한다고 하면 두 벡터 사이에는 반드시 각도 $\theta$ 가 존재 할 것입니다.
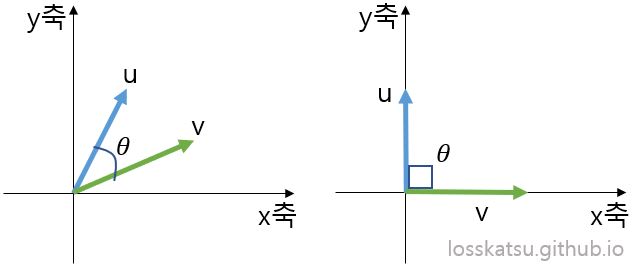
위 그림에서 좌측과 같이 두 벡터의 사이 각도가 90도보다 작을 수도 있고, 우측 처럼 두 벡터가 서로 수직인 경우도 존재합니다. (그림으로 표현하진 않았지만 각도가 90도 보다 큰 경우도 존재합니다.) 그리고 위에서 정의했던 내적을 아래와 같은 식으로 표현할 수 있습니다.
$ \mathbf{u} \cdot \mathbf{v} = \parallel \mathbf{u} \parallel \parallel \mathbf{v} \parallel cos\theta $
위 식을 이용하면 내적과 각도 $\theta$와의 관계를 알 수 있습니다.
- 내적 > 0 이면, $ \theta < 90 $
- 내적 < 0 이면, $ \theta > 90 $
- 내적 = 0 이면, $ \theta = 90 $
위 관계를 이용하면 두 벡터간의 위치관계를 알 수 있습니다. 예를 들어, 기준이 되는 벡터(A)에 다른 벡터(B)를 정사영 시킨다고 했을 때, 즉 내적했을 때 양수라면, 두 벡터 사이의 각도 $ \theta < 90 $ 이므로 벡터 B는 벡터 A 보다 각도 $ \theta < 90 $에 위치해 있다는 사실을 알 수 있겠죠. 특히 마지막 세번째관계에 주목할 필요가 있습니다. 만약 두 벡터를 내적했는데 값이 0이라면 두 벡터는 서로 수직임을 의미합니다. 따라서 내적은 두 벡터간의 수직 여부를 판단하는데 유용하게 쓰일 수 있습니다.
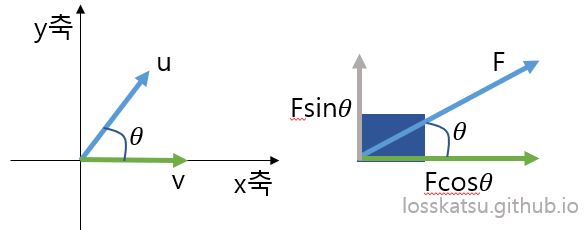
이를 물리학에서 말하는 일(Work), 힘(Force)의 관점에서 어떤 물체를 각도 $\theta$인 상태의 줄을 잡아당긴다고 하면, 위 관계가 조금 더 쉽게 이해 될 수 있습니다. 각도 $\theta$가 작을 수록 낭비되는 힘이 적으므로, 더 쉽게 물체를 움직일 수 있고, 같은 힘으로 물체를 더 멀리까지 이동시킬 수 있습니다. 반면 각도가 90도 보다 크다면 원래 움직이고자 하는 방향과 반대방향으로 움직이므로 내적은 음수가 됩니다. 그리고 90도 방향으로 줄을 잡아 당긴다면 물체는 움직이지 않겠죠. 내적의 공식이 각 성분 요소끼리 곱한 후 모두 더하는데요. 이것은 각 성분에 작용하는 모든 힘을 적용한 후 성분별 결과를 모두 더하는 것과 같습니다. 즉 이름그대로 Force를 구하는거죠. 어떤 물건에 힘을 작용했을 때 x1, x2, x3, …성분별로 힘(w1, w2, w3,…)을 적용시키고(곱하고), 성분별 힘 적용후 얼마나 움직였을 때를 모두 더하면 그 물체가 얼마나 움직였는지 알수 있습니다.(내적의 결과)
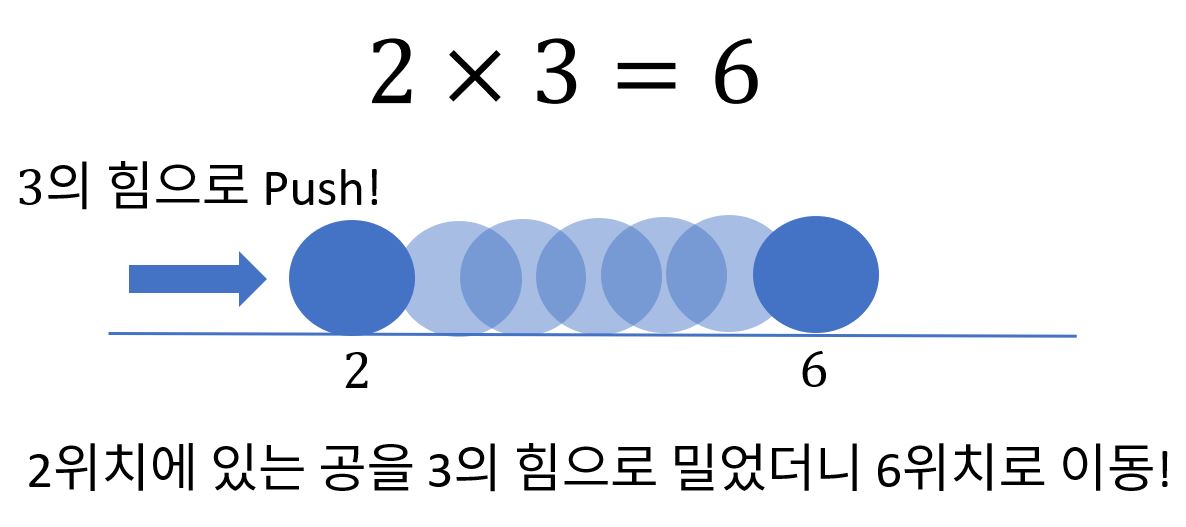
위 그림은 1차원 직선을 고려했을 때 내적의 설명이구요,
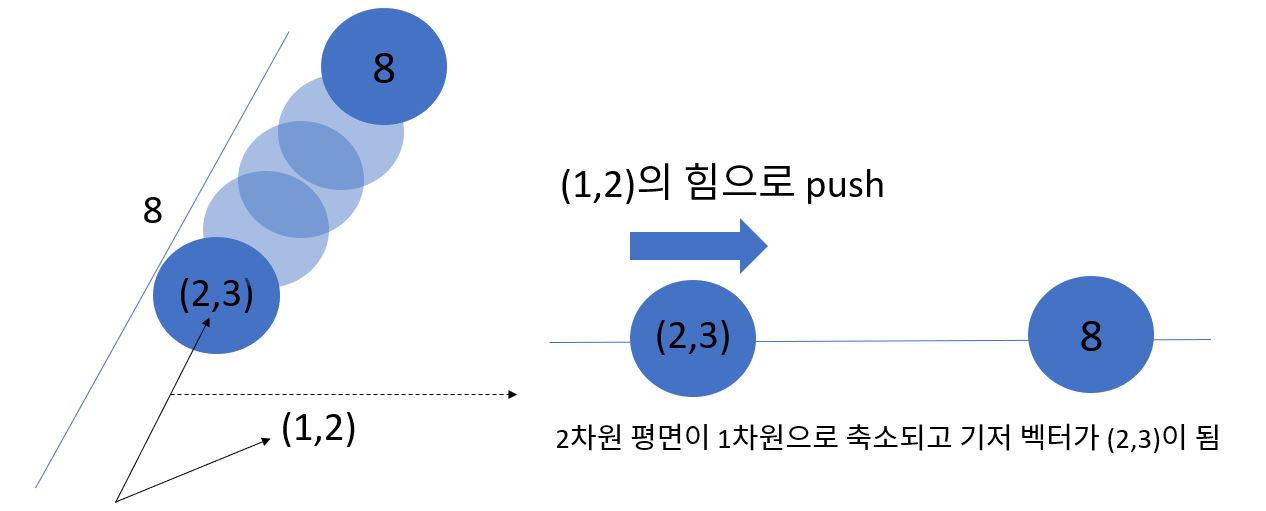
만약 좌표가 2차원이라고 합시다. (2,3)에 공이 위치해 있고 (1,2)를 내적한다고 하죠. 그럼 내적은 성분끼리 곱하고 모두 더하는 것이니, 2$\times$1 + 3$\times$2 =8 이 되는데요. 이 말은 x축 방향으로 2에 위치해있는 공에 1만큼 힘을 적용하고, y축 방향으로 3에 위치한 공에 2만큼 힘을 적용한 후 모두를 더하는 겁니다. 그럼 최종적으로 8에 위치해 있겠네요. 그런데 좀 이상합니다. 2차원 평면을 가정했고 공은 (2,3)에 위치하는데 최종 위치는 2차원 좌표가 아니고 그냥 8이라니요. 이것의 비밀은 내적을 한 후에 기저벡터가 바뀝니다. 즉, 원래 2차원 평면 기저였던 (0,1), (1,0)이 아니라, (2,3)이 기저벡터가 되는거죠(주의: 2,3까지의 거리가 1은 아닙니다.). 즉 (2,3)벡터방향으로 8만큼 움직인 것입니다.
이로 부터 우리는 아래와 같은 성질을 추가적으로 알 수 있습니다.
Cauchy-Schwarz Inequality
| $ | \mathbf{u} \cdot \mathbf{v} | \leq \parallel \mathbf{u} \parallel \parallel \mathbf{v} \parallel $ |
4.정사영 관점으로 보는 내적
위 개념은 정사영과 연관지을 수도 있습니다. 다시 한번 내적을 구하는 식을 보시죠.
$ \mathbf{u} \cdot \mathbf{v} = \parallel \mathbf{u} \parallel \parallel \mathbf{v} \parallel cos\theta $
위 식을 조금 변형하면
$ \parallel \mathbf{u} \parallel \parallel \mathbf{v} \parallel cos\theta = \parallel \mathbf{u} \parallel ( \parallel \mathbf{v} \parallel cos\theta ) $
혹은
$ \parallel \mathbf{u} \parallel \parallel \mathbf{v} \parallel cos\theta = ( \parallel \mathbf{u} \parallel cos\theta ) \parallel \mathbf{v} \parallel $
으로 표현 가능합니다. 위 식의 의미를 생각해보면 내적은 한 벡터를 다른 벡터에 정사영 시킨 후 각 벡터의 크기(길이)를 곱한다라고 생각할 수 있습니다.


