[선형대수] 선형변환(linear transformation)의 의미

선형변환(linear transformation)의 의미

참고링크

머신러닝	딥러닝	선형대수	기초통계	최적화
k-means	신경망이란	고유값,고유벡터	확률변수	컨벡스 셋
k-최근접이웃	성능함수	행렬식	확률분포	컨벡스 함수
선형회귀	신경망 학습	내적	모집단과 표본	라그랑주 듀얼
로지스틱회귀	교차연결	기저	평균과 분산	KKT 조건
릿지,라쏘회귀	합성곱 신경망	랭크, 차원	공분산, 상관계수	ROC 커브
의사결정나무	배치, 에포크 차이	선형변환	최대가능도추정	크로스 밸리데이션
서포트벡터머신	텐서플로기초(1)	직교행렬	베르누이,이항분포	실루엣 스코어
원클래스 SVM	텐서플로기초(2)	고유값분해	기하,음이항분포
LDA	seq2seq	특이값분해	초기하분포
GMM	opencv기초		포아송분포
부스팅	resnet		정규분포
사이킷런 실습	다각형내부판별		감마분포
	엣지판별		지수분포
			카이제곱분포
			베타분포
			균일분포

같은 사물도 어느 각도에서 보느냐에 따라 다르게 보일 수 있습니다. 마찬가지로 행렬이 주어졌을 때 어떤 각도로 보느냐에 따라 다르게 보일 수 있는데요. 기존 행렬을 데이터의 집합이나 나열이라는 느낌으로 바라보신 분이 계시다면, 오늘 다룰 선형변환은 형렬을 바라보는 새로운 각도일 수 있습니다. 우선 위키백과 정의 부터 보고 가시겠습니다.

선형변환은 선형 결합을 보존하는, 두 벡터 공간 사이의 함수이다.

심플한 정의네요. 위 정의에서 우리가 알아야 할 대목은, 1) 선형결합을 보존하는, 2) 두 벡터공간 사이의 함수 입니다. 지금부터 저와 하나씩 알아보도록 하겠습니다.

1. 선형결합을 보존한다의 의미

선형결합을 보존한다는 게 무슨 뜻일까요? 우선 선형결합의 뜻을 알아봅시다. 선형 결합이란 $T(u+v) = T(u)+T(v)$, $T(ku) = kT(u)$을 의미합니다.
그리고 선형결합을 보존한다는 뜻은 이러한 성질이 보존된다는 뜻입니다. 쉽게말해 덧셈과 곱셈에 닫혀있다라고 보시면 됩니다. 닫혀있다라는 말은 덧셈과 곱셈을 쓸 수 있다라는 뜻으로 생각하시면 편하실 것 같아요 (덧셈과 곱셈을 쓸 수 있는 판이 마련되어 있으니 마음껏 써라라는 뜻이기도 합니다, 실제로 우리가 일상생활에서 더하기 곱하기를 마음껏 쓰는 이유는 판이 마련되어 있기 때문이죠).

선형결합에 대해 좀 더 말씀드리면 어떤 벡터나 행렬을 나타낼 때 우리는 무의식적으로 기저를 정하고 그 기저를 근간으로 좌표를 생각합니다. (기저에 대해 복습하시려면 클릭) 예를 들면 (2,1)이라는 좌표는 무의식적으로 (1,0), (0,1)을 기저로 생성된 좌표라는 것이지요. 즉, (2,1)은 아래와 같은 표현식으로 이해할 수 있습니다.

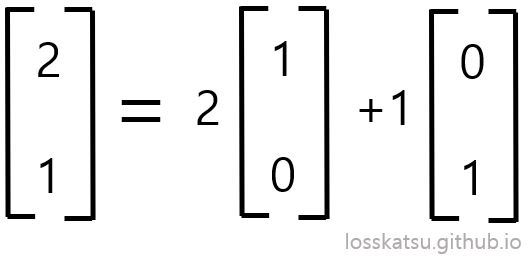
즉, 단순히 (2,1)이라는 벡터도 기저들의 선형결합이라는 뜻입니다. 그럼 기저가 달라지면 좌표도 달라질까요?

위 그림을 봅시다. 위 두개의 건물은 (1,0), (0,1)을 기저로 삼았을땐 꼭대기 층의 좌표가 다를 수 있습니다. 하지만 기울어진 건물의 경우, (1,0), (0,1)을 기저로 두었을땐 앞선 건물과 좌표가 달라지지만, 기저 또한 기울이게 되면 앞선 건물과 같은 좌표를 가질 수 있습니다. 즉, 서로 기저가 다른 경우, 같은 좌표를 가지더라도 같은 곳을 가리키는 것이 아니라는 뜻입니다.

2. 두 벡터 공간 사이의 함수

선형변환이란, 두 벡터 공간 사이의 함수라고 합니다. 만약 벡터 공간에 대해 잘 모르시는 분은 이전 포스팅을 참고해주세요. 두 벡터 공간 사이의 함수…선형변환은 결국 ‘함수’인데요. 위키백과에서 함수를 검색하면 아래와 같은 결과가 나옵니다.

첫 번째 집합의 임의의 한 원소를 두 번째 집합의 오직 한 원소에 대응시키는 이항 관계이다.

쉽게 말해, 한 점을 한 벡터공간에서 다른 벡터공간으로 이동시키는데 그 이동 규칙을 선형변환이라고 합니다. 예를 들어, 서울에 살고 있는 사람을 부산으로 이동시킨다는 규칙이 존재할 때, 그 규칙은 함수가 되고 해당 함수가 선형변환이라고 생각하시면 됩니다. 서울과 부산을 각기 서로다른 벡터 공간이라고 생각하시면 편할 것 같아요.

좀 더 수학적으로 표현하자면, 아래와 같은 행렬 $A$가 있다고 가정합시다.

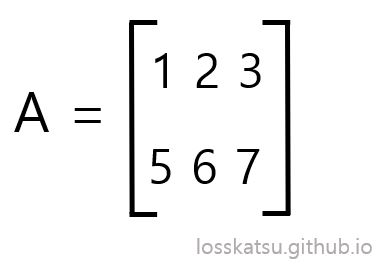
선형변환의 정의에 따르면 위와 같은 2X3 행렬은 3차원에서 2차원으로 선형변환 이라고 생각하시면 됩니다. 즉, 행렬 $A$에 임의의 행렬 $x$를 곱하는 $Ax$의 의미는 $x$라는 벡터를 3차원에서 2차원으로 변환 시키는 것이지요. 해당 선형변환의 결과 3차원 벡터 $x$는 2차원 벡터가 됩니다. 위에서 예로 들었던 서울에서 부산으로 이동시키는 예는 어떨까요, 실제로 서울과 부산은 같은 차원입니다. 그래서 서울에서 부산으로 변환 시키는 행렬이 있다면 그 행렬은 정방행렬이겠죠.

끝으로 선형변환의 위키백과 정의와 수학적 정의를 보고 마치겠습니다.

선형변환은 선형 결합을 보존하는, 두 벡터 공간 사이의 함수이다.

Definition 1. If T: V -> W is a mapping from a vector space V to a vector space W, then T is called a linear transformation from V to W if the following two properties hold for all vectors u and v in V and for all scalars k:
(1) T(ku) = kT(u)
(2) T(u + v) = T(u) + T(v)
In the special case where V=W, the linear transformation T is called a linear operator on the vector space V.