[머신러닝] 부스팅(boosting) 개념
업데이트:
부스팅(boosting) 개념
참고링크
부스팅 정의
본 포스팅은 MIT 6.034 Artificial Intelligence 수업을 참고하여 작성하였습니다.
기계학습에서 부스팅은 주로 편향을 줄이고 지도학습의 차이를 줄이기 위한 앙상블 메타 알고리즘이며, 약한 학습모델을 강한 학습모델로 변환하는 기계학습 알고리즘 제품군입니다.
일반적인 머신러닝은 하나의 방법을 이용하지만 부스팅은 여러가지 방법들이 작동하는 것입니다. 예를 들어 분류기 h가 있다고 합시다. 이 분류기 h는 [-1,+1]로 분류를 하는데요. 예를들어 +1이면 커피, -1이면 차라고 합시다. 그리고 분류기의 에러율은 아래와 같습니다.
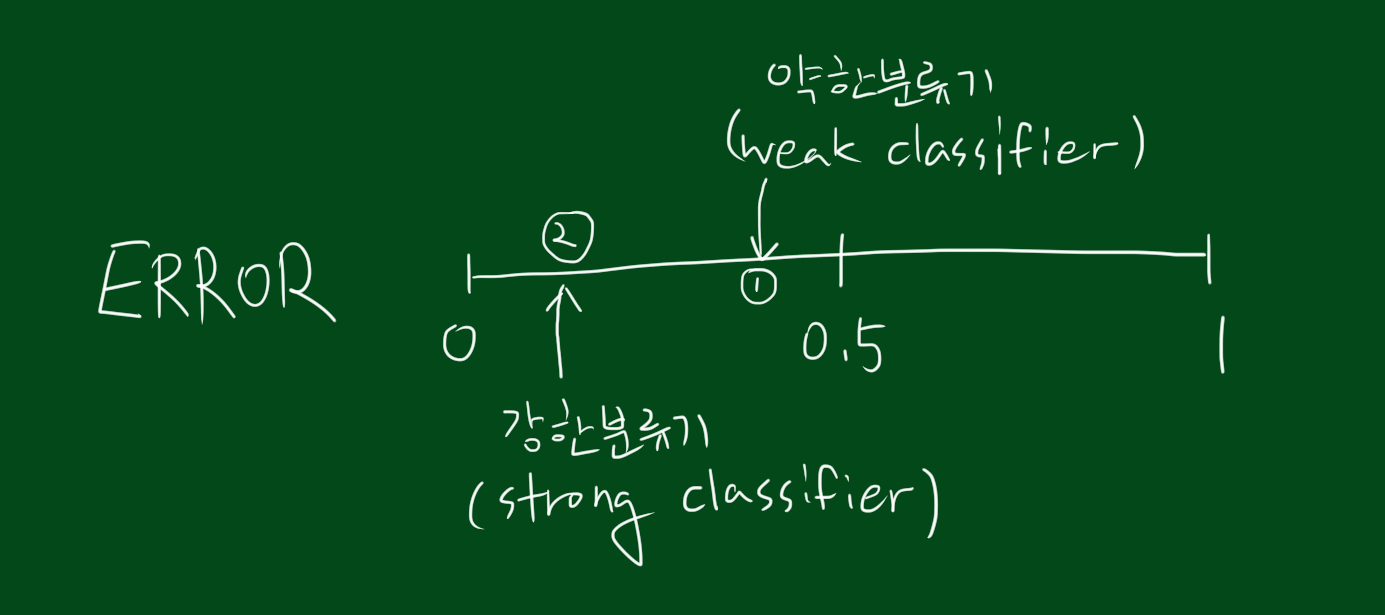
위 그림대로 에러는 0에가까울수록 좋습니다. 위 그림에서도 당연히 0에 가까운 분류기가 더 좋은 분류기 이고, 에러율이 0.5에 가깝다는건 사실 동전던지기보다 조금 나은 수준인데, 이를 좋은 분류기라고 부리긴 힘들죠.
강한 분류기 = 약한 분류기의 합
하지만 약한 분류기라도 여러개를 합한다면 강한 분류기가 될 수 있습니다.
\[H(x) = sign(h^{1}(x)+h^{2}(x)+h^{3}(x))\]위 식에서 $h^{1}(x), h^{2}(x), h^{3}$는 약한 분류기이고 $H(x)$는 약한 분류기 셋을 합한 큰 분류기 입니다. 만약 3개중에 2개의 분류결과가 일치한다면 맞는 결과를 낼 수 있습니다. 물론 3개중 3개가 일치하면 더 좋겠죠. 3개중 2개만 맞춰도 되는 이유는 $H(x)$는 기호만 불러오기 때문입니다. 이 말은 하나의 분류기가 틀린다해도 나머지 두개의 분류기가 맞춘다면 괜찮다는 뜻입니다.
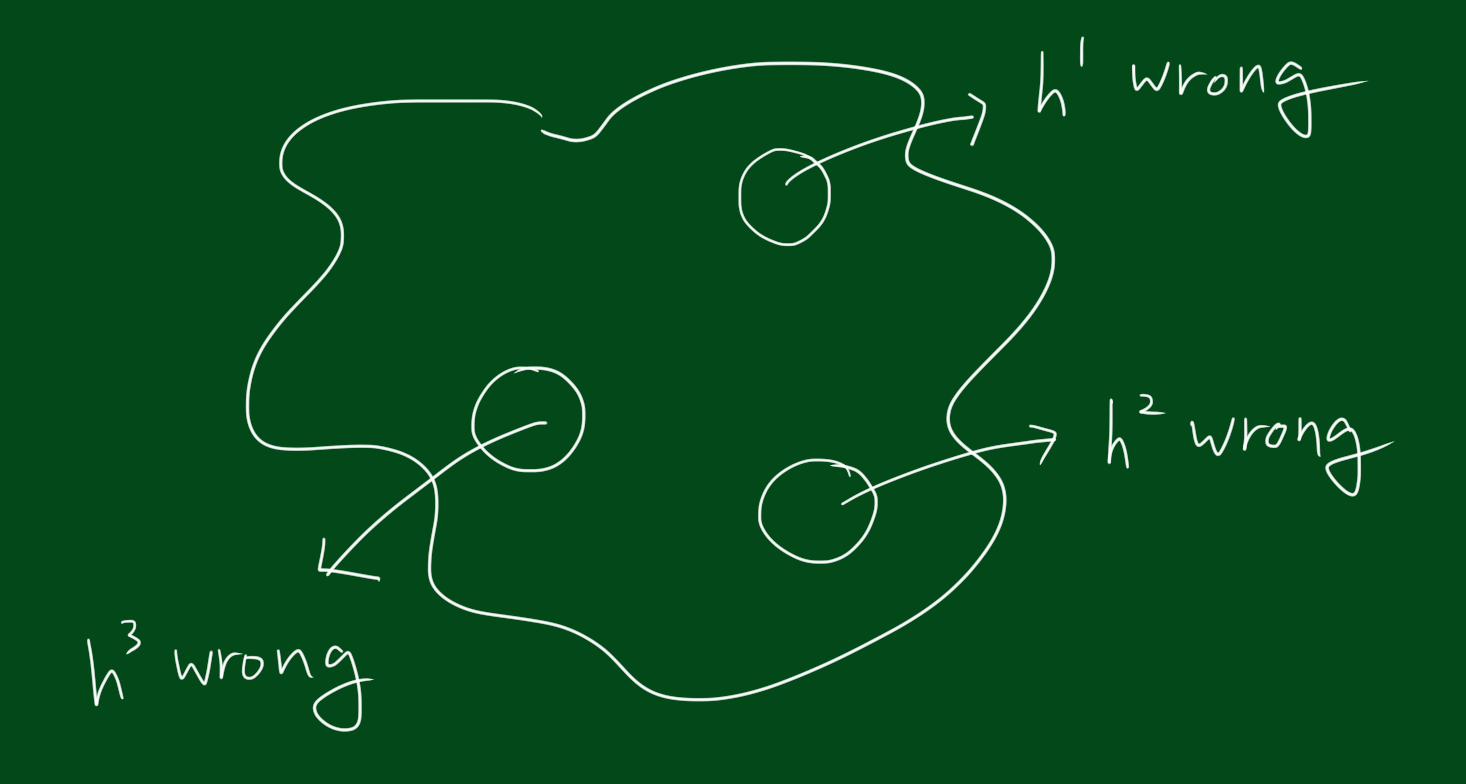
위 그림은 전체공간에서 각 분류기가 잘못된 결과를 내는 영역을 표시한 그림입니다. 만약 영역이 위와 같다면 모든 데이터셋에 대해 틀릴 수가 없습니다. 왜냐하면 하나가 틀려도 나머지 둘은 맞출테니까요. 지금까지우리는 h들의 결과가 +1인지 -1인지보고 그것들을 다 더해서 부호를 결정하면 각각 테스트한 결과값보다 더 나은 결과를 얻을 수 있을지 알고 싶은 것입니다. 하지만 위와 같은 영역만 존재할 수 는 없습니다. 아래 그림처럼 각 분류기별로 잘못된 결과를 내는 영역이 겹칠수 있습니다.
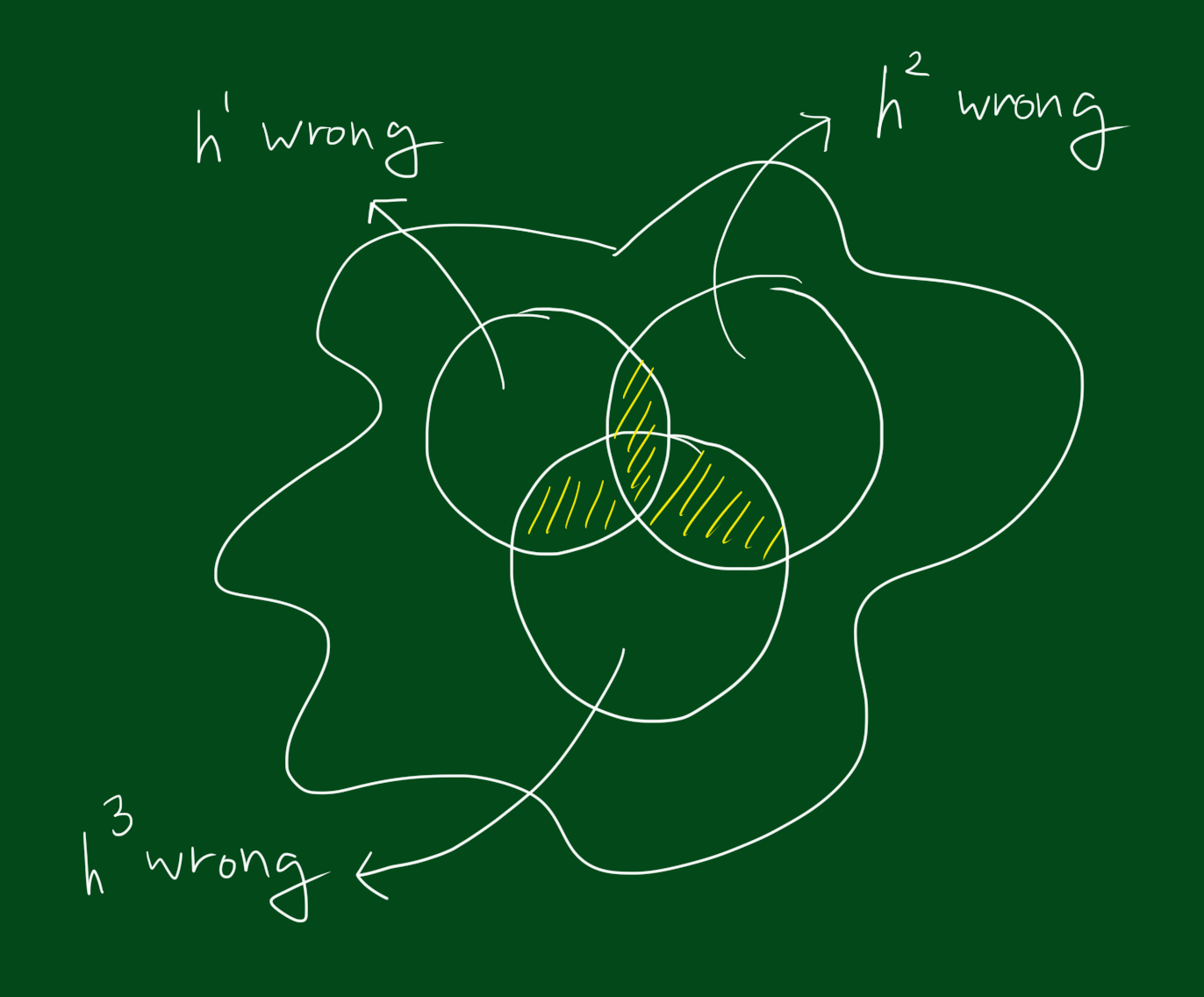
위와 같은 경우는 운이 나쁜 경우에는 3개의 테스트 결과를 합친것이 하나의 테스트 결과만도 못하는 경우가 생길 수 있습니다. 자, 그럼 위와 같은 상황을 해결할 수 있는 알고리즘을 만들어봅시다.
1.새로운 h1
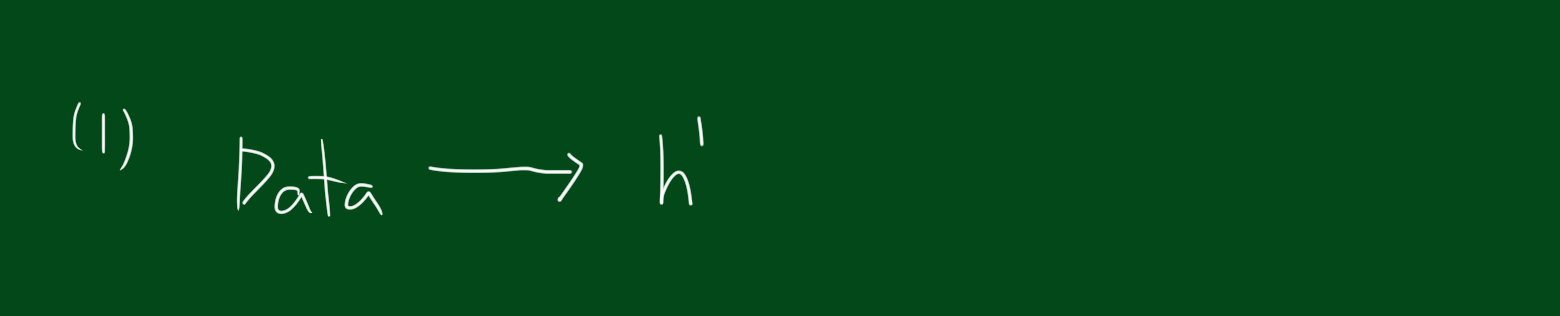
위와 같은 상황을 해결하기 위해 가장 먼저할 일은 데이터를 토대로 $h^{1}$을 만드는 것입니다. 모든 데이터에 대해 테스트해보고 어떤것이 가장 적은 에러율을 나타내는지 본후 $h^{1}$을 선택합니다. 가장 적은 에러율을 보여주는 분류기를 선택했다 할지라도 에러율이 0이긴 힘듭니다. 다음 단계는 에러의 원인, 즉 분류실패한 데이터를 강조하는 단계입니다.
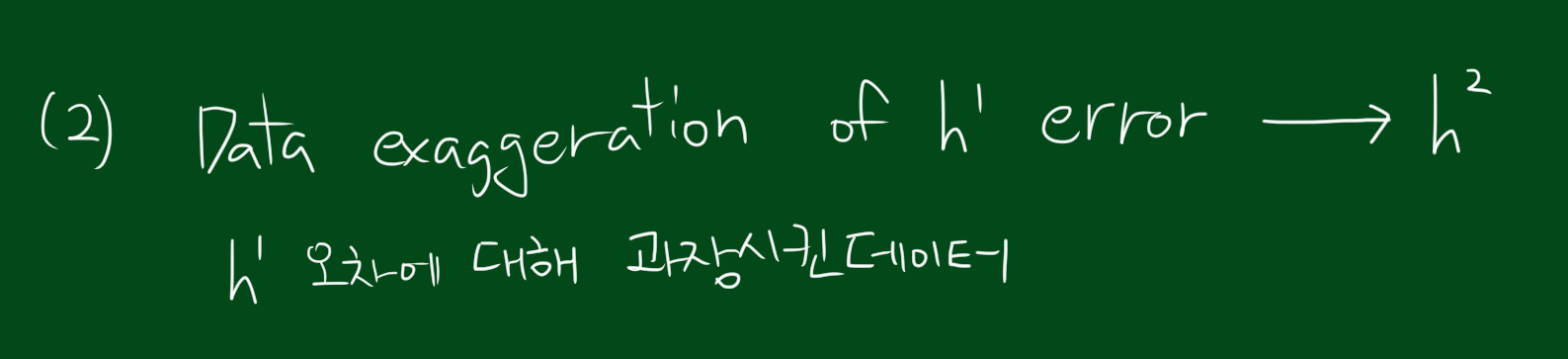
다음단계는 $h^{1}$에 대해 에러를 내는 경우 그냥 고려하지 않고, 왜곡된 데이터를 사용할 것입니다. 여기서는 아까 $h^{1}$에 대해 에러를 내는 경우의 데이터에 대해서 더 큰 영향을 미치도록 하는 것입니다. 즉, 그 틀린 예시들에 대해 조금더 가중치를 주거나, 몇배를 곱하거나 하는 방식을 써서 말이죠. 이렇게 $h^{1}$에서 오차를 낸 예시들에 대해 조금더 주의를 기울여 $h^{2}$를 만듭니다. 이렇게하면 분류기는 $h^{1}, h^{2}$ 두개가 됩니다.

이제 분류기가 두개가 되었으니 이 두 분류기의 결과가 다른 경우가 있을 것입니다. 마지막 단계는 위 두 분류기의 결과가 다른 경우에 해당하는 데이터에 가중치를 줘서 분류기 $h^{3}$을 구하는 것입니다.
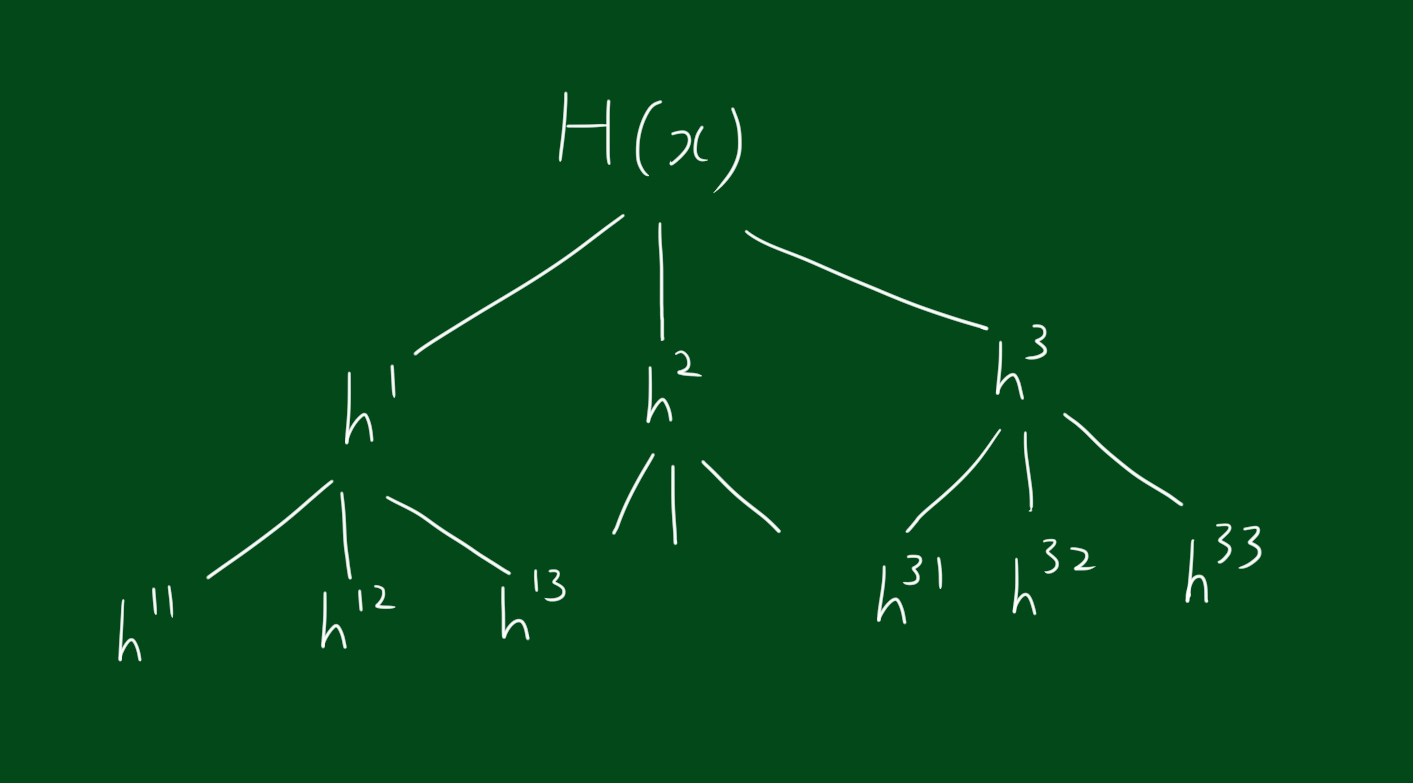
사실 위에서 큰 H가 작은 분류기 h들의 합으로 나타낼수있다고 했지만, 좀 더 생각해보면 사실 그 작은 h들도 더 작은 분류기의 합일 수 있습니다.
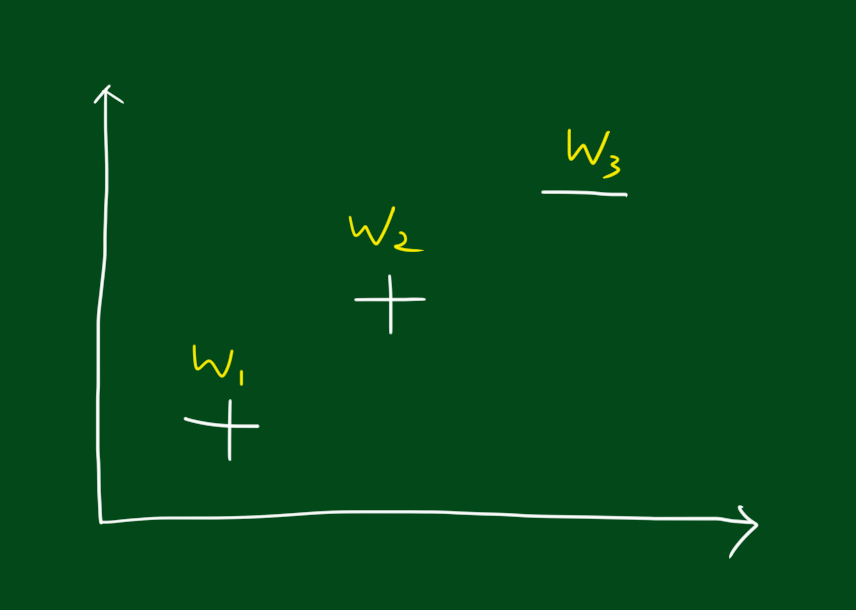
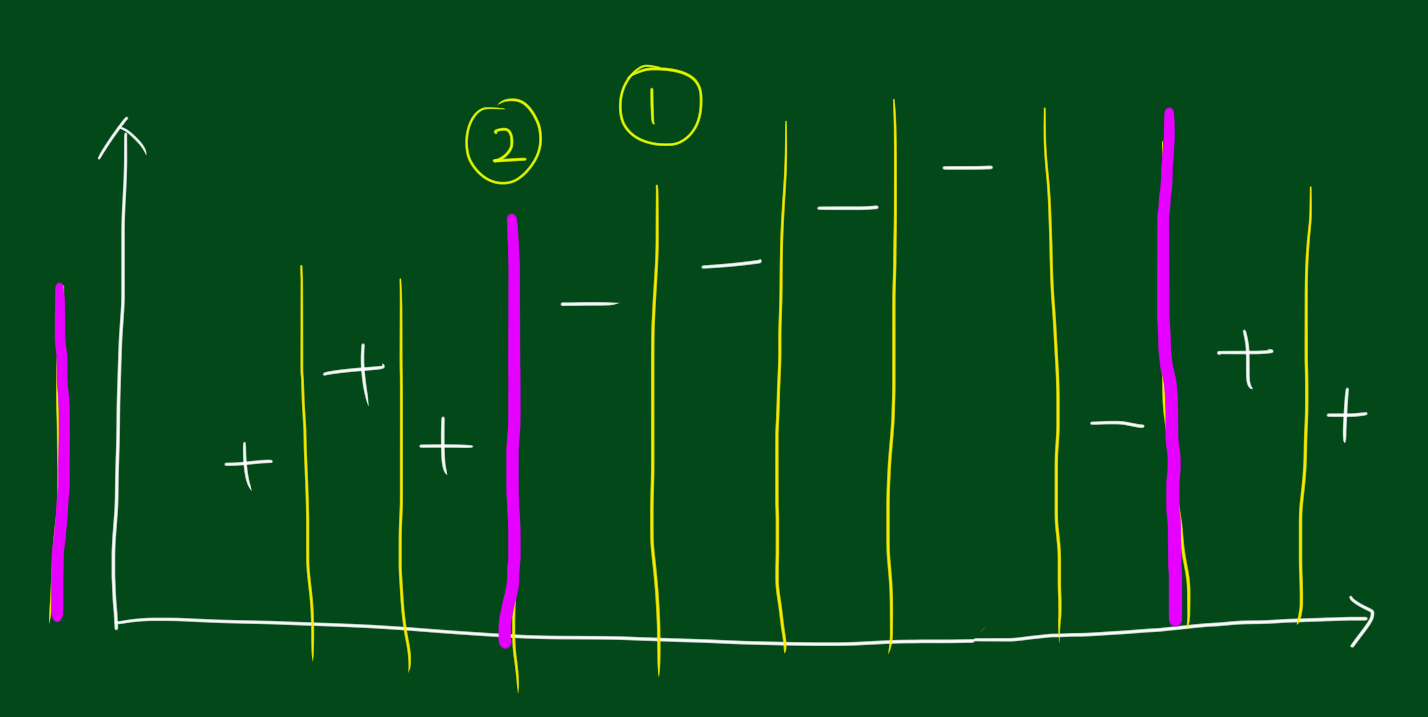
위와 같은 데이터를 분류한다고 해봅시다. 분류를 위해 결정 그루터기 방법(decision tree stumps)을 쓸껀데요.
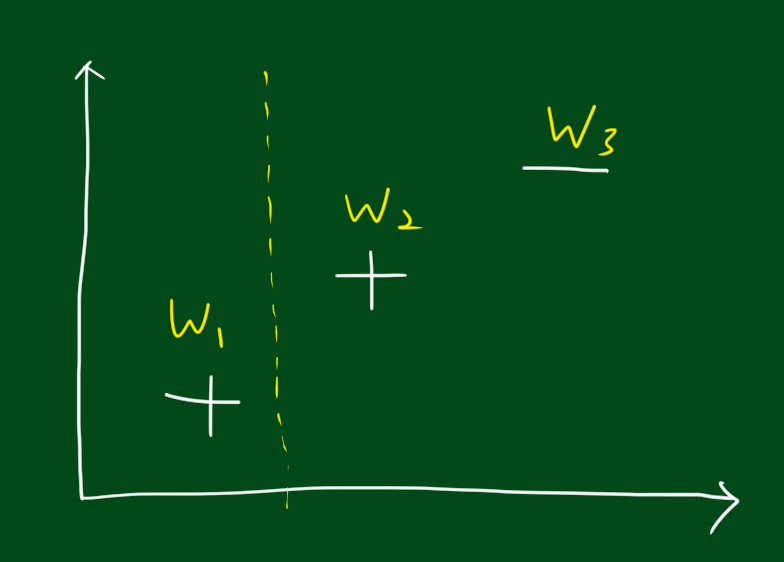
위 그림 처럼 경계선을 긋는 것이 하나의 분류 기준이 될 수 있습니다. 경계선을 기준으로 오른쪽은 +, 왼쪽은 -라고 분류하는 거죠.
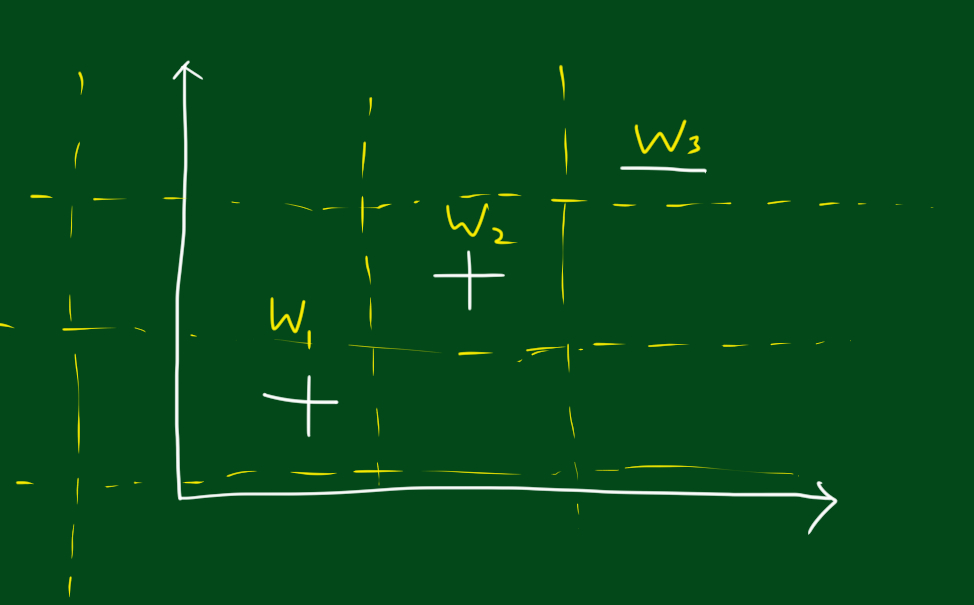
이런식으로 분류선을 그을수있는 경우는 많습니다. 여기서 집고 넘어가야할 부분은, 부스팅을 쓰기 위해서는 결정그루터기 방법을 써야할까요? 그렇지 않습니다. 여러분은 어떤 분류기에 대해서라도 부스팅을 사용할 수 있습니다. 결정그루터기 대신 k최근접이웃, 신경망, 의사결정나무 등 아무거나 넣으시면 됩니다. 부스팅의 기본 개념은 어떤 모형을 넣어도 상관 없다는 것입니다. 위에서 결정그루터기를 예로든건 단지 예일 뿐이죠.
에러율
자, 그래서 위에서 우리가 그린 각 선이 분류한 결과에 대해 에러율은 얼마일까요? 에러율은 아래 식을 따릅니다.
\[E = \sum_{wrong}\frac{1}{N}\]처음에는 가중치를 주지 않습니다.
\[w_{i}^{1}=\frac{1}{N}, \epsilon = \sum_{wrong}w_{i}\]현재 단계에선 가중치를 주지 않고, 틀린 갯수만 세는 것입니다. 이 단계 이후에 가중치를 줄 수 있는데, 모든 공간에서 가중치의 합은 1이 되어야합니다.
\[\sum w_{i} = 1\]큰 분류기 만들기
다음단계는 작은 분류기들을 종합하는 것인데요. 사람들은 H(x)라는 분류기를 여러단계로 나누어 아주 작은 분류기들을 포함하도록 만드는 방법을 갭라하기 시작했습니다.
\[H(x) = sign(\alpha^{1}h^{1}(x)+\alpha^{2}h^{2}(x)+\alpha^{3}h^{3}(x)+\dots)\]위 식에서 $h^{1}(x)$는 첫번쨰로 뽑은 분류기 h라는 뜻입니다. 자, 이제 우리는 모든 예시들이 같다고 생각하지 않을 것입니다. 각각의 분류기들은 오류를 일으키는 서로다른 공간을 가지고 있는데요. 그러므로 어떤 예시들에는 더 가중치를 줘야하고 더 전문적인 분류기를 골라야합니다.
반복
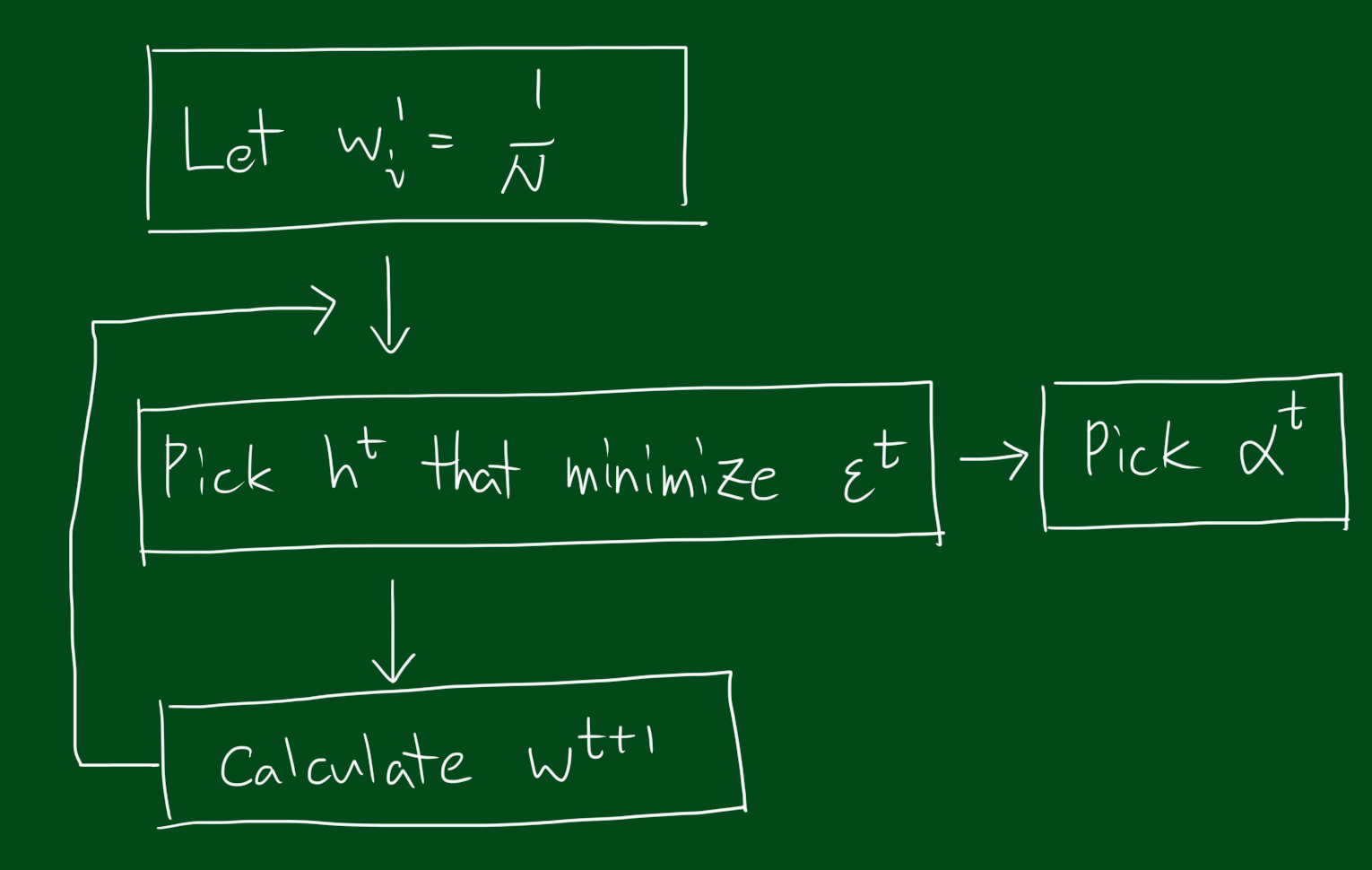
즉, 위와 같은 단계를 거칩니다.
새로운 가중치 구하기
새로운 가중치는 아래와 같은 식을 통해 얻어집니다.
\[w_{i}^{t+1} = \frac{w_{i}^{t}}{z}exp(-\alpha^{t}h^{t}(x)y(x))\]위 식에서 y는 갑자기 어디서 나왔을까요? 위 식에서 y는 svm의 y와 같습니다. h(x)가 정답을 맞추면 y는 +1, 틀리면 y는 -1이 됩니다. h(x)가 정답을 낸다면 h와 y는 같은 부호를 가지게 되면서 곱하면 +1이 되고, 반대로 h(x)가 틀린답을 낸다면 -1을 곱하는 것이됩니다. 즉, y는 잘못된 답을 냈을 때 부호를 바꾸는 역할을 합니다. 또한 위 식에서 z는 정규화(normalizer)시키는데 사용됩니다. 만약 $\frac{w_{i}^{t}}{z}$를 쓰지 않고 $w_{i}^{t}$를 사용하면 단계를 거치면서 가중치 합이 1이 되지 않습니다. 즉 normalizer z를 사용함으로써 가중치 합을 1로 유지할 수 있습니다.
최소 에러
Minimum error bound for whole thing if
\[\alpha^{t} = \frac{1}{2}ln\frac{1-\epsilon^{t}}{\epsilon^{t}}\]다음에 할일은 t에서 $\alpha$를 알아내는 식을 t에서의 에러율을 가지고 구하는 것입니다. 위 식을 가중치 구하는 식에 넣어봅시다.
진짜 새로운 가중치
\[w_{i}^{t+1} = \frac{w_{i}^{t}}{z}\times \sqrt{\frac{\epsilon^{t}}{1-\epsilon^{t}}}\]위 가중치는 정답을 맞추었을 경우 입니다.
\[w_{i}^{t+1} = \frac{w_{i}^{t}}{z}\times \sqrt{\frac{1-\epsilon^{t}}{\epsilon^{t}}}\]위 가중치는 정답을 맞추지 못했을 경우 입니다. 자, 이렇게 정답을 맞췄는지 못맞췄는지에 따라 새로운 가중치 w에 대한 식을 구했습니다.
z를 구하자
다음으로 노멀라이저 z를 구해보겠습니다.
\[\sqrt{\frac{\epsilon^{t}}{1-\epsilon^{t}}}\sum_{correct}w_{i}^{t} + \sqrt{\frac{1-\epsilon^{t}}{\epsilon^{t}}}\sum_{wrong} w_{i}^{t}=z\]따라서 z는 아래와 같습니다.
\[z = 2\sqrt{\epsilon^{t}(1-\epsilon^{t})}\]다 합치자
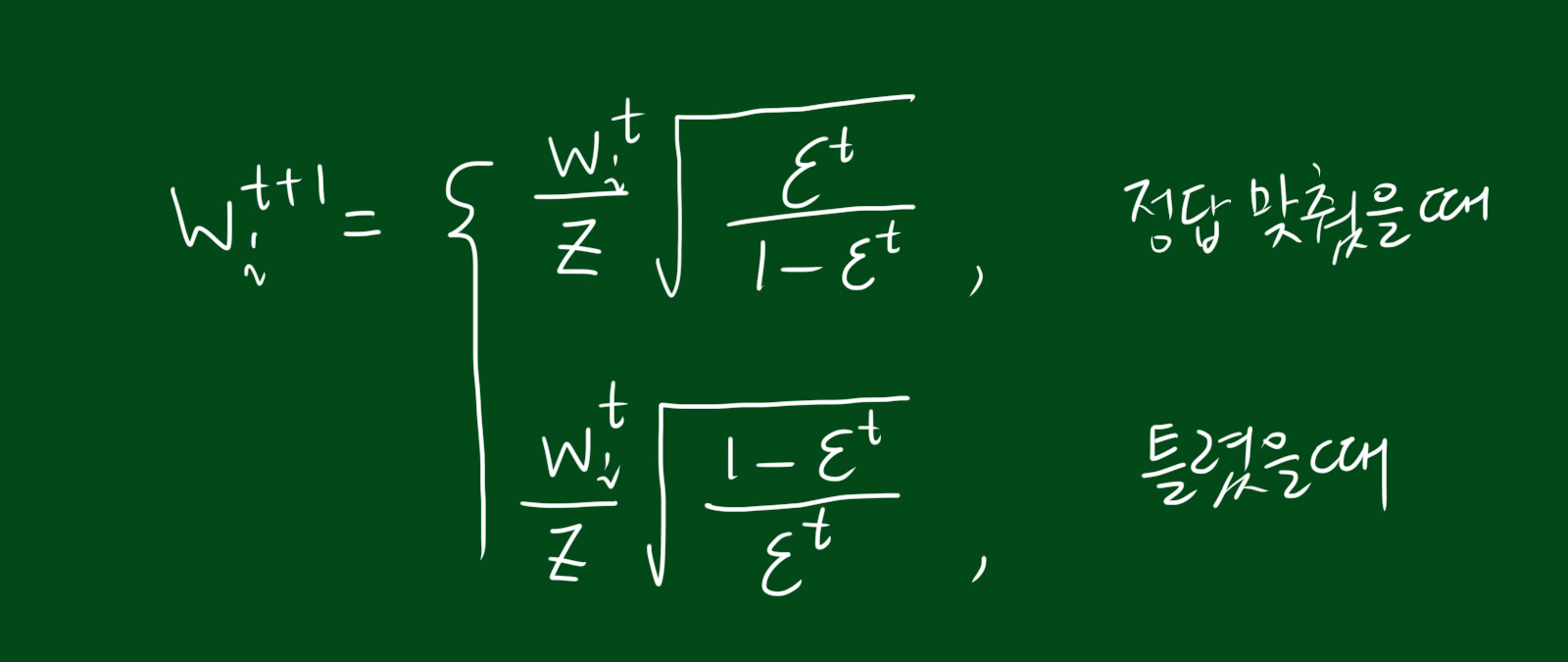
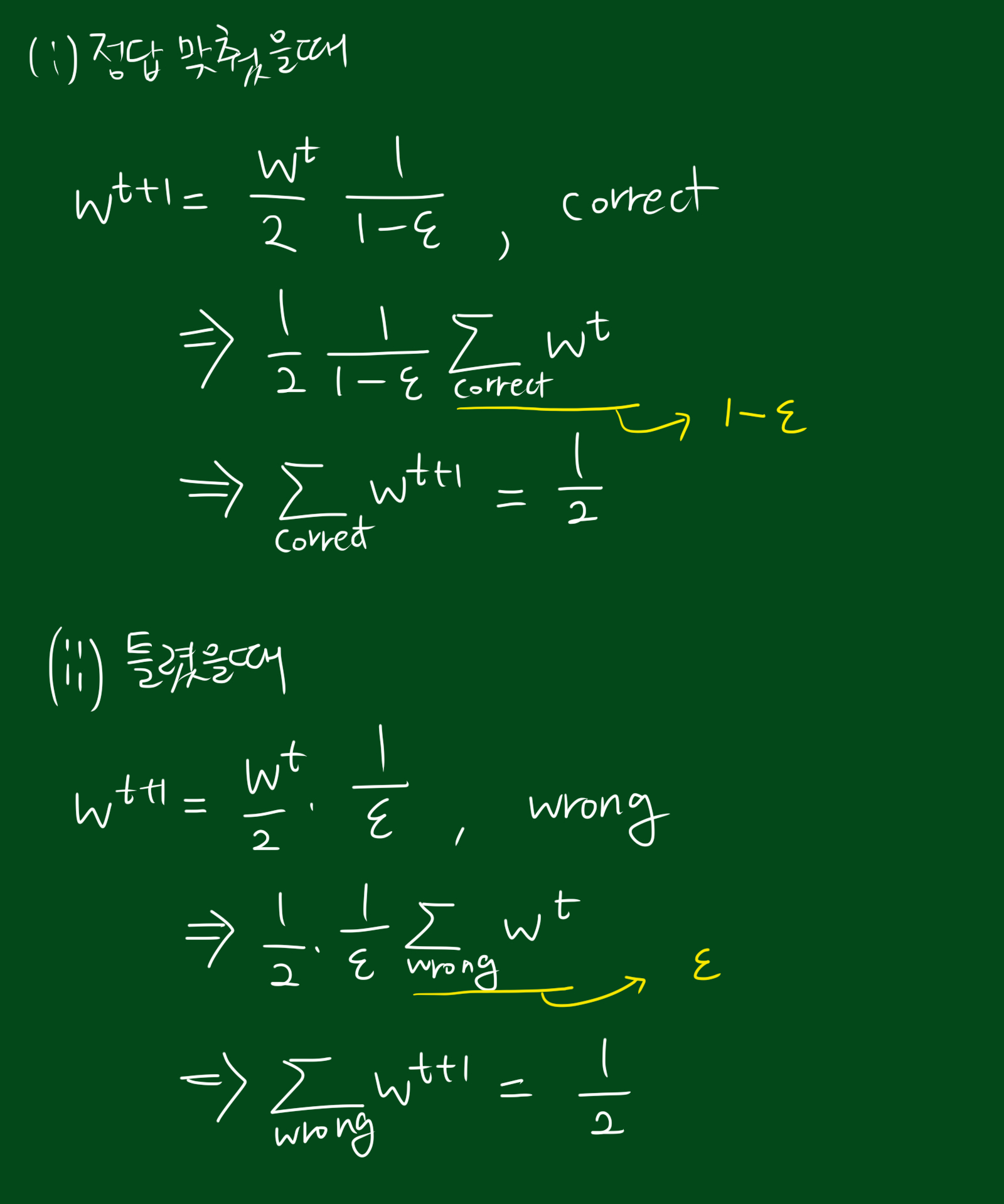
그렇다면 이 w를 분류기가 정답을 내는 공간에서 모두 더하면 어떻게 될까요? 이 말은 이전의 테스트에서 정답을 낸 모든 경우의 가중치를 모두 더할 수 있다는 뜻입니다. 그리고 그 다음 단계에서의 가중치를 알아내기 위해서는 절반이 되도록 값을 매기면 됩니다. 가중치들의 합은 이전 가중치의 축소된(scaled) 버전인 것이죠. 자, 이제 이 새로운 분류기는 최소의 가중치를 계산했습니다. 여러분은 그저 맞는 예시들을 찾아서 그 가중치를 모두 더해서 1/2로 축소하면 됩니다. 이제 여러분은 로그를 계산할 필요도 없고, 자연상수 e를 계산할 필요도 없고, z를 계산할 필요도 없으며, 새로운 가중치를 계산하기 위해 $\alpha$를 계산할 필요도 없습니다. 그저 우리가 할 일은 축소(scaled)하는 것 뿐입니다. 아주 편하죠. 이것이 thank-god hole 1 입니다.
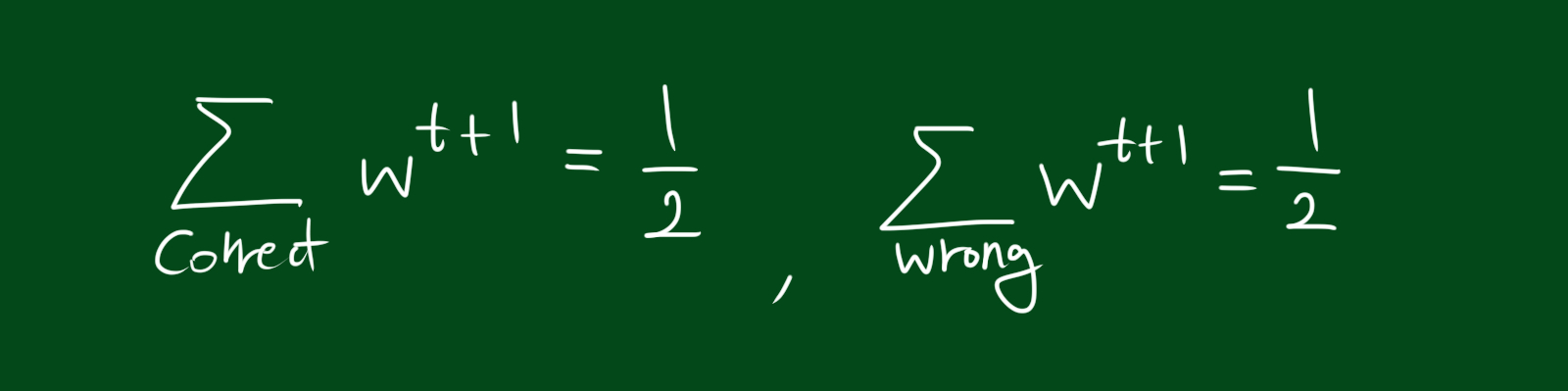
이런 경우는?
그렇다면 이래와 같은 상황은 어떨까요?
위 공간에서 나눌수 있는 방법은 많습니다. 하지만 실질적으로는 3가지 방법 밖에 없습니다. 이말은 즉, 부스팅을 위해 고려해야하는 상황이 중요한 테스트는 몇개 안된다는 것입니다.
과적합
과적합(overfitting)에 대해선 어떨까요? 데이터를 기반으로 모델링을 했으니 과적합이 생기지 않았을까요? 하지만 놀랍게도 부스팅을 사용하면 과적합이 생기지 않습니다. 이건 실험적인 결과인데요. 학계를 혼란에 빠뜨렸죠. 그리고 이 현상을 설명하기 위해 연구중입니다.


