[최적화]컨벡스 함수(Convex function)의 개념
업데이트:
[최적화] 컨벡스 함수(Convex function)의 개념
참고링크
1. 정의역(domain, 도메인)
함수 $f$가 다음과 같다고 합시다.
\[f: \mathbb{R}^{p} \rightarrow \mathbb{R}^{q}\]이 때, 함수 $f$의 정의역(domain)을 $\mathbf{dom}\, f$라고 쓰겠습니다. 위 함수의 의미는 함수 $f$는 $\mathbb{R}^{p}$ 공간에 속하는 벡터 $p-vector$를 취한 후, $\mathbb{R}^{q}$ 공간에 속하는 벡터 $q-vector$를 반환합니다.
2. Convex
만약 $\mathbf{dom}\, f$가 컨벡스 셋(convex set)이고, 모든 $x$와, $y\in \mathbf{dom}\, f$, $0\leq \theta \leq 1$에 대해
\[f(\theta x + (1-\theta)y) \leq \theta f(x) + (1-\theta)f(y)\]를 만족하는 함수 $ f: \mathbb{R}^{n} \rightarrow \mathbb{R} $를 컨벡스(convex)하다라고 말합니다. 위 부등식의 의미는 두 점 $(x, f(x)), (y, f(y))$ 사이의 line segment, 즉, 두점사이의 현(chord)이 함수 $f$의 그래프보다 위쪽에 놓여있어야합니다. 위 부등식을 그림으로 표현하면 아래와 같습니다.

만약 위 부등호가 아래와 같이 등호가 없고(strict inequality),
\[f(\theta x + (1-\theta)y) < \theta f(x) + (1-\theta)f(y)\]$0 < \theta < 1$이면 strictly convex하다고 말합니다. 또한 $-f$가 convex하다면 $f$는 concave하다고 말합니다. 마찬가지로 $-f$가 strictly concave하다면 $f$는 strictly convex하다고 말합니다.
참고로 아핀함수(affine function)는 컨벡스 조건 부등식을 만족하므로, 아핀함수는 convex이고 concave합니다. 반대로, 어떤 함수가 convex이고 concave하다면 해당 함수는 아핀함수 입니다.
3. First-order conditions
$f$가 미분가능하다는 말은 $\mathbf{bol}\, f$내의 모든 점들에 대해, 해당 점의 그래디언트(gradient) $\bigtriangledown f$가 존재한다는 뜻입니다. $f$가 미분가능하다고 할때, 함수 $f$가 convex하다는 말은 곧 $\mathbf{bol} \, f$가 컨벡스하며
\[f(y) \geq f(x) + \bigtriangledown f(x)^{T}(y-x)\]위와 같은 부등식이 $\mathbf{bol}\, f$내 모든 점 $x, y$에 대해 만족한다는 말과 같습니다. 위 부등식을 그림으로 표현하면 아래와 같습니다.
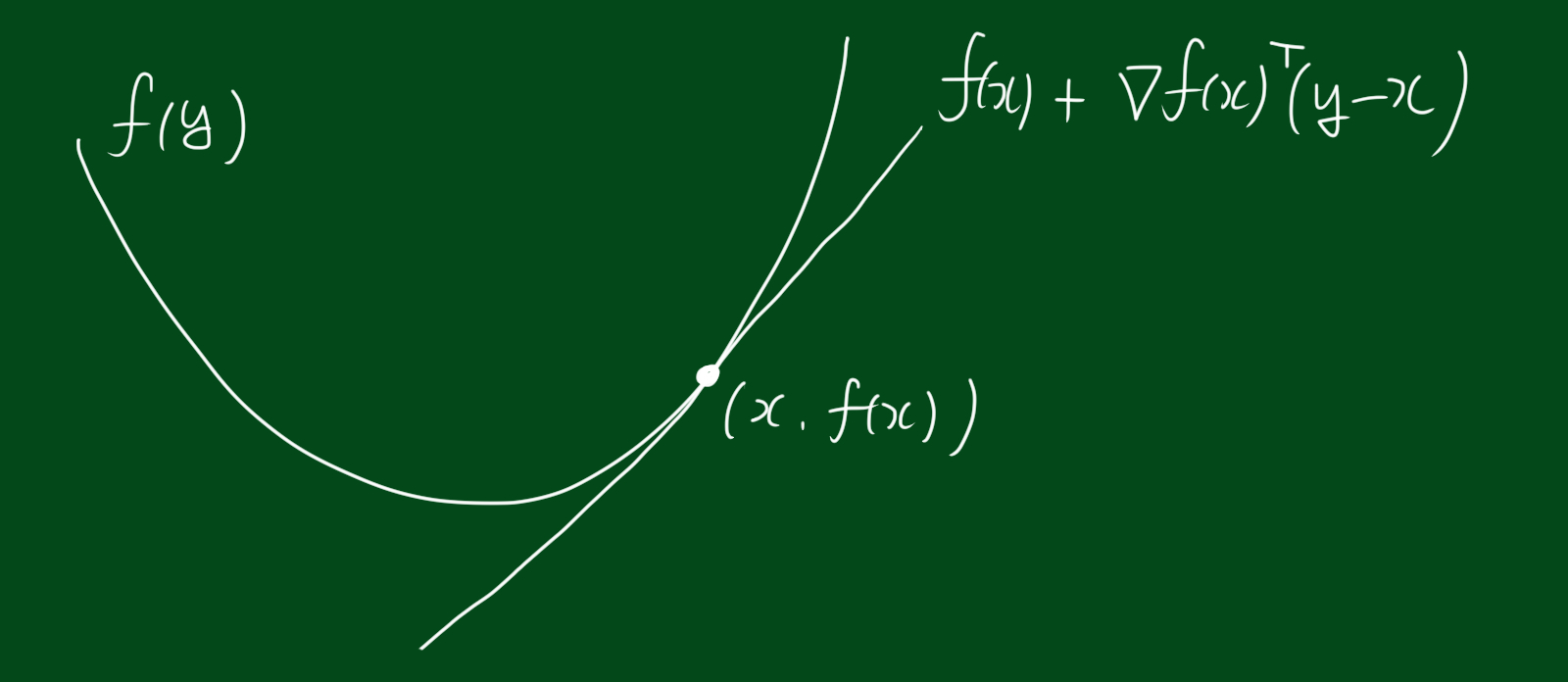
위 부등식이 의미하는 것은 컨벡스 함수에 대해 local information을 보여주며, 이로부터 우리는 global information을 유도할수 있다는 것입니다. 예를들어 , $\bigtriangledown f = 0$일때, 모든 $y \in \mathbf{dom} f$에 대해, $f(y) \geq f(x)$라면, $x$는 함수 $f$에 대한 global minimizer입니다.
strict convexity 위와 같은 형식으로 표현할 수 있습니다. 만약 $\mathbf{dom}\, f$가 컨벡스이고 $x, y \in \mathbf{dom}$일 때,
\[f(y) > f(x) + \bigtriangledown f(x)^{T}(y-x)\]위 부등식을 만족하면 strict convex하다고 말합니다. 그리고 $\mathbf{dom}\, f$가 컨벡스이고
\[f(y) \leq f(x) + \bigtriangledown f(x)^{T}(y-x)\]이면 concave하다고 말합니다.
4. Second-order conditions
만약 함수 $f$가 두번 미분가능해서 $\bigtriangledown^{2}f$가 존재할때,
\[\bigtriangledown^{2}f(x) \geq 0\]이면 함수 $f$는 컨벡스하다고 말합니다. 반대로
\[\bigtriangledown^{2}f(x) \leq 0\]하다면 함수 $f$는 concave하다고 합니다.
5. Jensen’s inequality
가장 처음에 언급했던 부등식
\[f(\theta x + (1-\theta)y) \leq \theta f(x) + (1-\theta)f(y)\]을 Jensen’s inequality라고도 부릅니다. 이를 좀더 일반화 하면 아래와 같이 쓸수 있습니다.
\[f(\theta_1 x_1 + \cdots + \theta_k x_k) \leq \theta_1 f(x_1) + \cdots + \theta_k f(x_k)\]이때, $x_1, \dots, x_k \in \mathbf{bol}\, f$이며, $\theta_1, \dots, \theta_k \geq 0$이고 $\theta_1 + \cdots + \theta_k =1$입니다. Jensen’s inequality를 응용해 흔히 사용되는 부등식 중 하나는 아래와 같습니다.
\[f(E(x)) \leq E(f(x))\]위 부등식에서 E는 Expectation, 즉, 기대값을 의미합니다. 또한 아래와 같이 간단한 부등식도 있습니다.
\[f(\frac{x+y}{2}) \leq \frac{f(x)+f(y)}{2}\]6. Convex 성질이 보존되는 경우
6.1 Nonnegative weighted sums
우선 $f$가 컨벡스일때, $\alpha \geq 0$에 대해 $\alpha f$ 또한 컨벡스합니다. 또한 $f_1, f_2$가 모두 컨벡스일때, 두 함수의 합 $f_1 + f_2$또한 컨벡스합니다. 이를 조합하면 아래 조건을 만족하는 함수 $f$는 컨벡스하다는 것을 알 수 있습니다.
\[f = w_1 f_1 + \cdots + w_m f_m\]6.2 Composition with an affine mapping
만약 $f$가 컨벡스하다면
\[g(x) = f(Ax+b)\]위 조건을 만족하는 $g$또한 컨벡스합니다.
7. Conjugate function
$f: \mathbb{R}^{n} \rightarrow \mathbb{R}$일 때,
\[f^{\ast} = sup_{x\in \mathbf{dom}\, f}(y^{T}x - f(x))\]위와 같은 함수 $f^{\ast}: \mathbb{R}^{n} \rightarrow \mathbb{R}$는 함수 $f$의 conjuate라고 합니다.
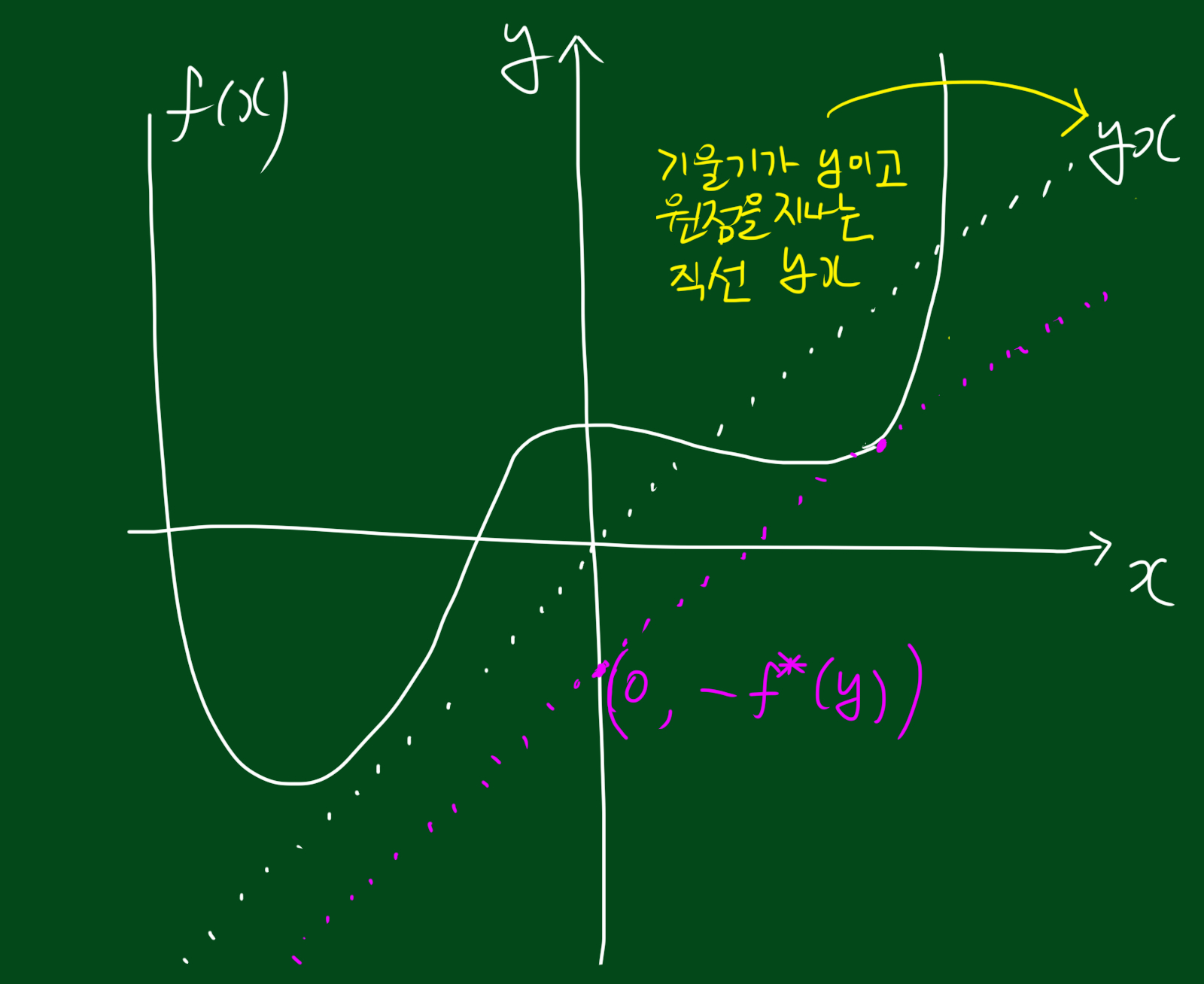
위 그림을 통해 conjugate를 정의해보겠습니다. conjugate 함수 $f^{\ast}$는 선형함수 $yx$와 $f(x)$간의 maximum gap을 의미합니다. 만약 $f$가 미분가능하다면 이는 $f\prime(x)=y$에서 발생합니다.


