[최적화]컨벡스 셋(Convex set)의 개념
업데이트:
[최적화] Convex set의 개념
참고링크
1. line segment
$\mathbb{R}^n$ 공간에서의 두 점 $x_1, x_2$가 있다고 합시다. 이 때 두 점 $x_1, x_2$을 잇는 선(line) 사이에 있는 점 $y$를 아래와 같이 표현합니다.
\[y = \theta x_1 + (1-\theta)x_2\]만약 $\theta = 0$이면 $y=x_2$가 되고, $\theta = 1$이면 $y=x_1$이 됩니다. 이때, $ 0 \leq \theta \leq 1$이면 $x_1, x_2$간의 line segment라고 합니다.
위 식은 아래와 같이 바꿔쓸수 있습니다.
\[y = x_2 + \theta(x_1-x_2)\]위 식을 해석해보면, $y$는 base 지점 $x_2$과 $x_1-x_2$ 방향(direction)에다가 $\theta$만큼 스케일(scale)한 값의 합으로 표현할수 있다는 것입니다.
2. 아핀 셋(affine set)
특정 집합(set) $C\subseteq \mathbb{R}^n$이 아핀(affine)이라는 말은 아래와 같습니다. $C$ 속의 두 점을 잇는 직선이 있다고했을 때, 즉, $x_1, x_2 \in C$이고 $\theta \in \mathbb{R}^n$ 일 때, $ \theta x_1 + (1-\theta) x_2 \in C $s이면 $C$는 아핀 셋(affine set) 입니다. 여기서 주목해야할 점은 $\theta$값에 제한이 없다는 뜻입니다.
이를 2차원 이상으로 확장시키면 $\theta_1 x_1 + \cdots + \theta_k x_k$, $\theta_1+\cdots+\theta_k = 1$으로 쓸 수 있는데 이를 포인트 $x_1, \dots, x_k$에 대한 아핀 결합(affine bombination)이라고 합니다. 즉, 아핀 셋(affine set)은 해당 아핀 셋의 포인트에 대한 모든 아핀 결합을 포함합니다. 즉, 집합 $C$는 집합 $C$에 속하는 두 점의 선형 결합(linear combination)입니다. 이 때, 선형 결합 계수 $\theta$들의 합은 1입니다.
3. 컨벡스 셋(convex set)
만약 $C$의 두 점사이의 line segment가 집합 $C$에 속한다면 집합 $C$는 컨벡스(convex) 합니다. 다른 말로하면, 두 점 $x_1, x_2 \in C$에 대해 $0\leq \theta \leq1$를 만족하는 $\theta$에 대해 아래 조건을 만족하면 집합 $C$는 컨벡스(convex) 합니다.
\[\theta x_1 + (1-\theta)x_2 \in C\]좀더 러프하게 말하면, 컨벡스 셋이란, 어떤 집합내의 모든 두 점들을 서로 이었을 때, 해당 직선 또한 집합내에 속해야한다는 뜻입니다. 컨벡스의 정의에서는 아핀과는 다르게 $\theta$값의 범위 제한이 있습니다.
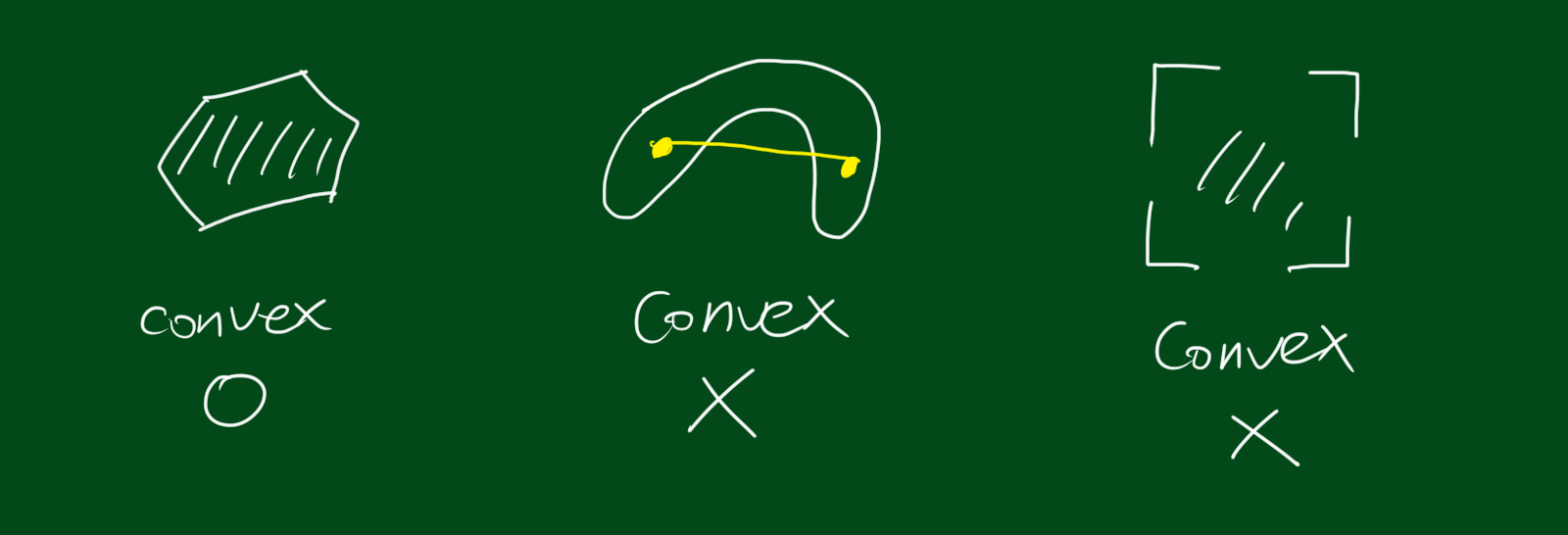
모든 아핀 집합은 컨벡스입니다. 왜냐하면 아핀 셋은 두 지점 사이의 모든 점을 포함하므로 두 점 사이의 모든 line segment를 포함하기 때문입니다.
4. 초평면(hyperplane)
초평면(hyperplane)은 아래와 같은 형태의 집합을 말합니다.
\[\{ x | a^T x = b \}\]이 때, $a \in \mathbb{R}^n$이고, $a \neq 0$이며, $b \in \mathbb{b}$입니다. 해석학에서 초평면은 선형 방정식에서 솔루현의 형태입니다. 기하학에서 초평면은 초평면의 점들에 벡터 $a$를 내적한 집합으로 해석합니다. 또는 normal vector $a$에 대한 초평면이라고 부릅니다. 이 때, $b \in \mathbb{R}$는 초평면과 원점사이의 차이(offset) 결정합니다. 위 초평면의 형태를 아래와 같이 바꿔보겠습니다.
\[\{ x | a^T (x-x_0) = b \}\]이 때, $x_0$는 초평면 내의 어떠한 점도 가능합니다. 이를 그림으로 그리면 아래와 같습니다.
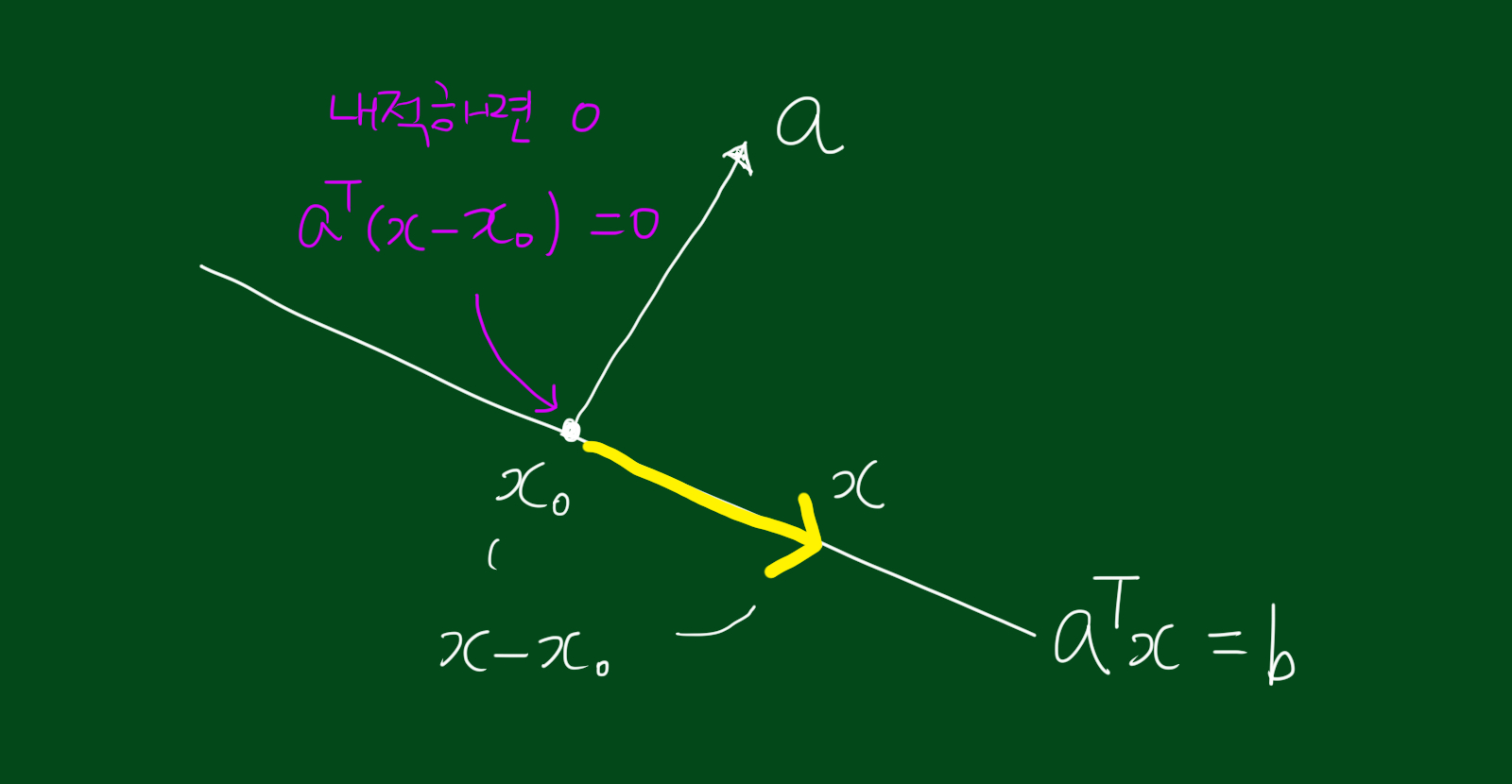
위 그림을 토대로 표현방법을 아래와 같이 바꿀수도 있습니다.
\[\{ x | a^T (x-x_0) = 0 \} = x_0 + a^{\bot}\]위 식에서 $a^{\bot}$는 $a$의 orthogonal complement입니다. 즉, 모든 orthogonal 한 벡터의 집합은 아래와 같이 표현할 수 있습니다.
\[a^{\bot} = \{ a^{T}v = 0 \}\]이 말인 즉슨, 초평면은 오프셋(offset) $x_0$에 벡터 $a$에 orthogonal한 모든 벡터를 더한 값이 됩니다.
5. 반공간(halfspace)
전체 공간 $\mathbb{R}^{n}$은 초평면(hyperplane)에 의해 두 반공간(halfspace)으로 나눠집니다. 반공간은 아래와 같은 형태로 표현합니다.
\[\{ a^{T}x \leq b \}\]반공간은 컨벡스(convex)이지만 아핀(affine)은 아닙니다. 이를 그림으로 표현하면 아래와 같습니다.
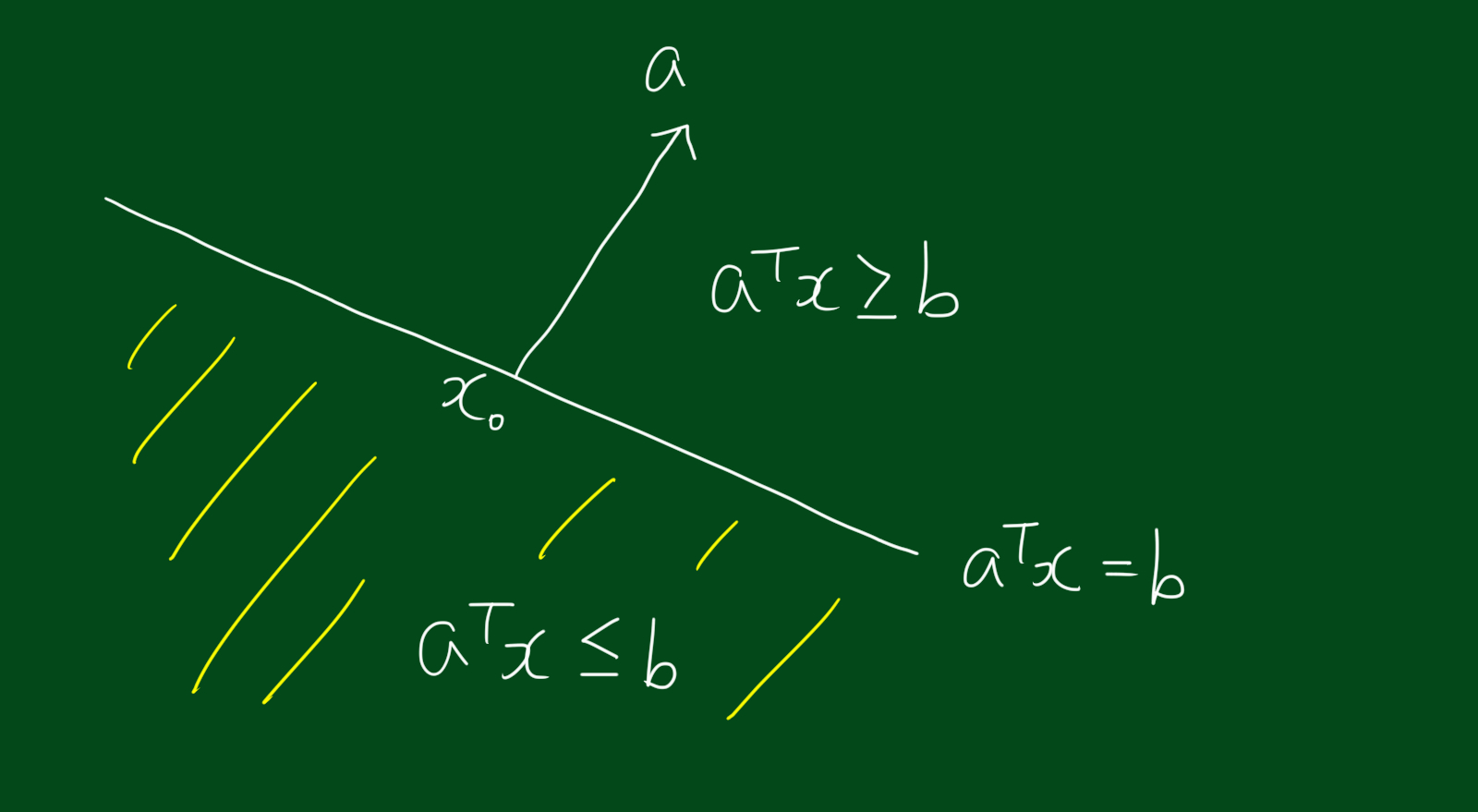
6. 유클리디안 볼(Euclidean ball)
$\mathbb{R}^{n}$내에서 유클리디안 볼(Euclidean ball)은 아래와 같이 표현합니다.
\[B(x_c, r) = \{ x | \Vert x - x_c \Vert_{2} \leq r \} = \{ x| (x-x_c)^{2}(x-x_c) \leq r^2 \}\]이 때, $r>0$ 이며, $\Vert u \Vert_{2} = (u^{T}u)^{\frac{1}{2}}$ 입니다.(Euclidean norm) $x_c$는 ball의 중심을 나타내며 $r$은 반지름(radius)을 나타냅니다.

유클리디안 볼은 컨벡스 셋(convex set)입니다. 만약 $\Vert x_1 - x_c \Vert_{2} \leq r$, $\Vert x_2 - x_c \Vert_{2} \leq r$이고 $0 \leq \theta \leq 1$이면,
\[\begin{align} \Vert \theta x_1 + (1-\theta)x_2 \Vert_{2} &= \Vert\theta(x_1-x_c)+(1-\theta)(x_2-x_c) \Vert_{2} \\ &\leq \theta\Vert x_1-x_c \Vert_{2} + (1-\theta)\Vert x_2 - x_c \Vert_{2} \\ &\leq r \end{align}\]이와 연관된 컨벡스셋을 타원체(ellipsoid)라고 하는데, 이는 아래와 같이 표현합니다.
\[\mathcal{e} = \{ x | (x-x_c)^{T}P^{-1}(x-x_c) \leq 1 \}\]이 때, $P$는 대칭행렬(symmetric)이며, positive definite입니다. $P$가 의미하는 것은 중심 $x_c$로부터 모든 방향으로 얼마나 뻗어나가는 지를 의미합니다.


