[머신러닝] 의사결정나무(decision tree) 개념
업데이트:
의사결정나무(decision tree) 개념
참고링크
의사결정나무의 정의
본 포스팅은 MIT 6.034 Artificial Intelligence 수업을 참고하여 작성하였습니다.
의사결정나무(decision tree)는 어떤 항목에 대한 관측값과 목표값을 연결시켜주는 예측 모델이다. 트리 모델 중 목표변수가 유한한 수의 값을 가지는 것을 분류 트리라 한다. 이 트리구조에서 잎은 클래스 라벨을 나타내고 가지는 클래스라벨과 관련있는 특징들의 논리곱을 나타낸다ㅏ. 결정 트리 중 목표 변수가 연속하는 값, 일반적으로 실수를 가지는 것은 회귀 트리라고 한다.
의사결정나무의 정의는 위와 같습니다.
의사결정나무가 필요한 데이터
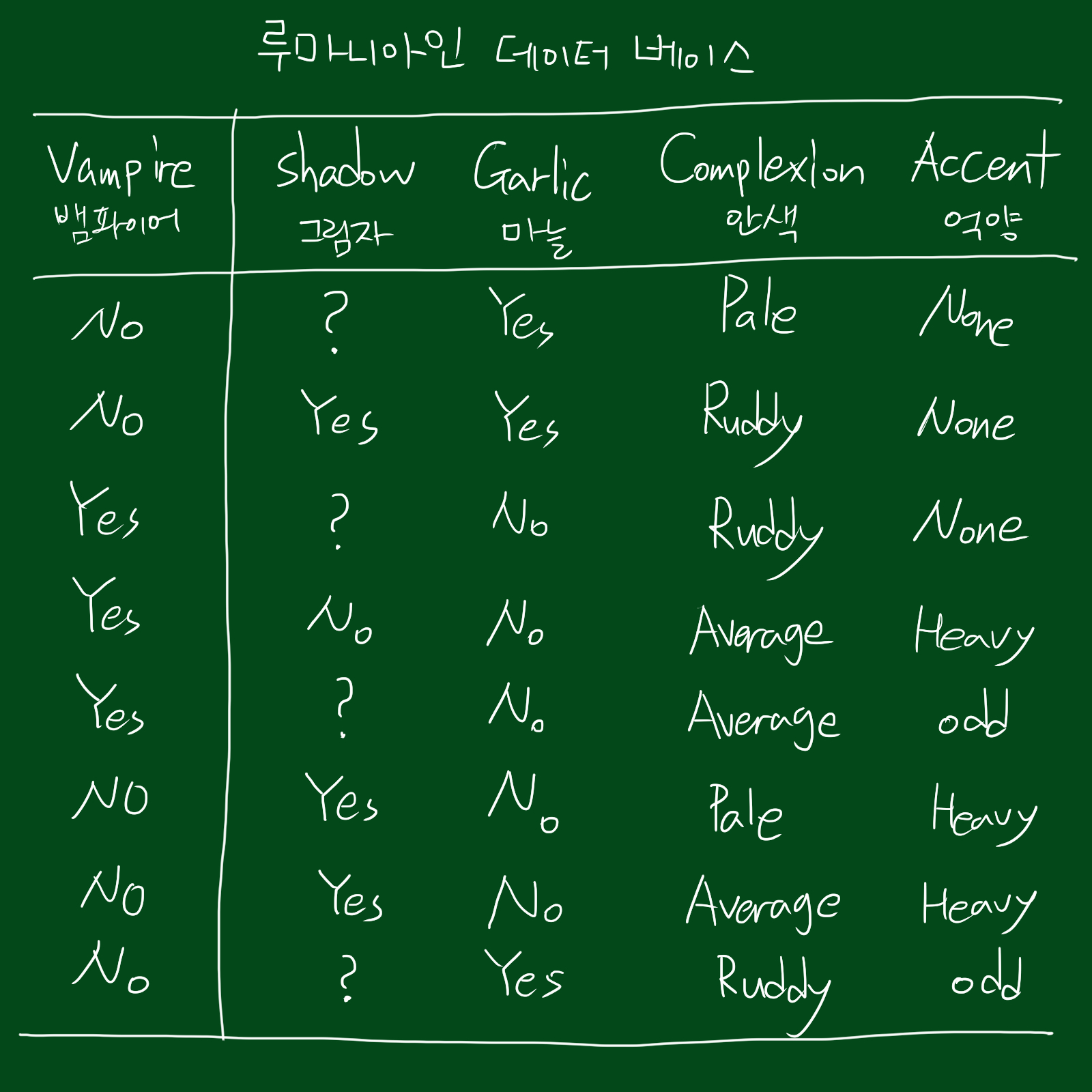
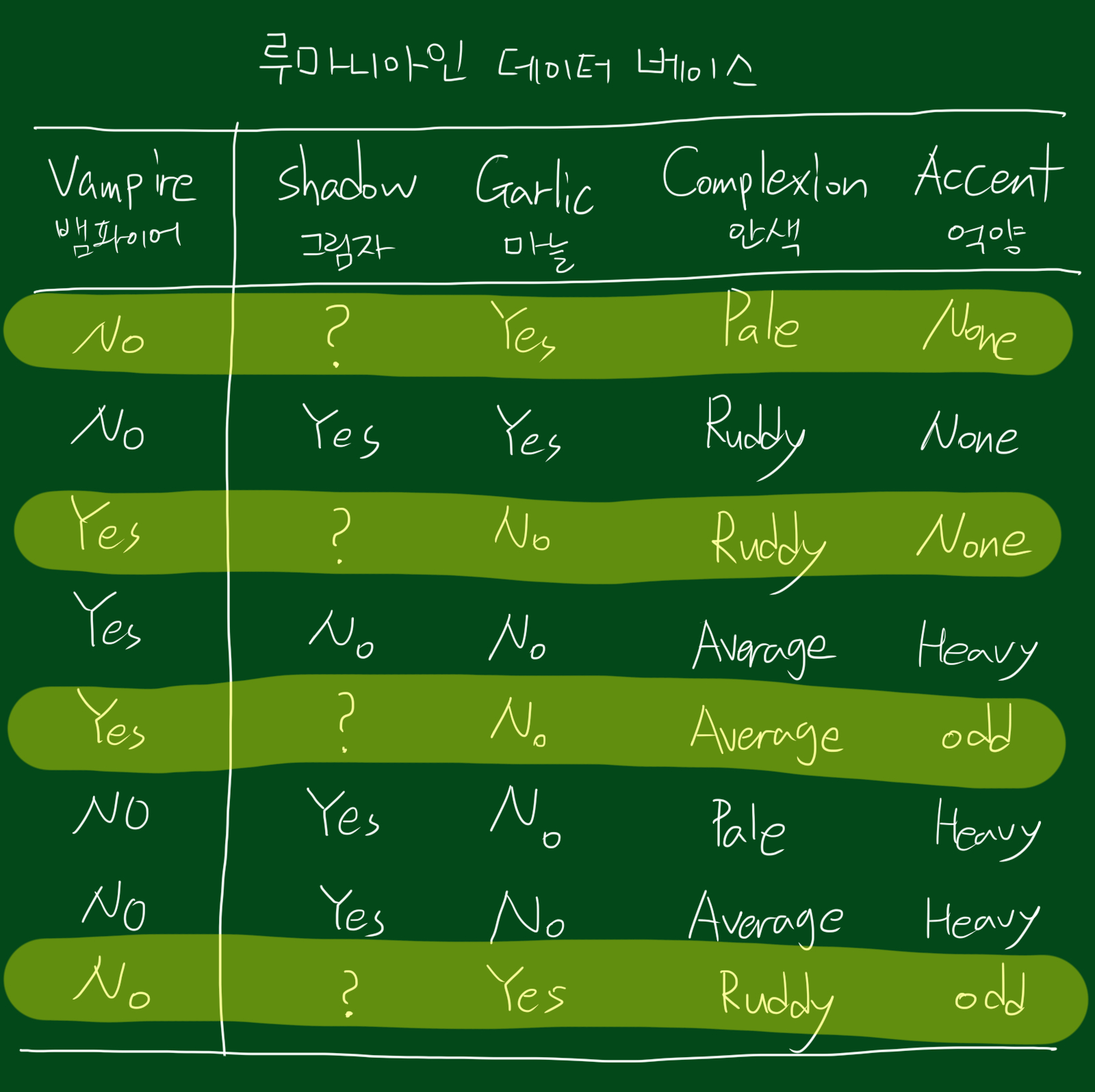
위와 같은 데이터셋이 있다고 합시다. 이 데이터는 루마니아인을 대상으로 뱀파이어인지 아닌지에 대한 데이터베이스입니다. 이런 데이터셋을 다룰 때의 문제는 변수가 수치데이터가 아니라는 것입니다. 즉, non numeric이라는 것인데요. 따라서 모든 특성이 의미 있는지 없는지를 알기 힘듭니다. 또한 비용문제도 있는데요. 테스트할때 다른 테스트보다 공수가 많이 들어갑니다. 위 데이터를 예로 들면 실제로 실험참가자에게 마늘을 먹여봐야하기 때문이죠.

이런 데이터를 다를 때는 테스트를 하게 되는데요. 하나의 테스트를 선택하면 그에 따른 결과를 볼 수 있습니다. 또한 위 그림에서 볼수있듯, 하나의 테스트결과가 또다른 테스트가 되는 경우도 있습니다. 즉, 테스트를 어떻게 배치하느냐가 중요합니다.
좋은 의사결정나무란?
좋은 트리(tree)란 최사한의 테스트를 하는 트리입니다. 즉, 작은 트리라는 것이죠. 작은 트리를 만들고 싶은 이유는 비용감소로 인해 효율적이기 때문입니다. 예를들어 단 한번의 테스트로 뱀파이어인지 아닌지를 구분할 수 있다면 그보다 쉬운 방법은 없을 것입니다. 작은트리가 선호되는 또다른 이유는 오컴의 면도날(Occam’s Razor)입니다. 가장 간단한 설명이 종종 최적의 설명이 되곤하죠.
작은 트리?
작은 트리라는 말은 트리 밑단의 결과에 동종집단들끼리 몰려 있다는 것입니다. 즉, 한쪽에는 모두 일반인, 다른 한쪽에는 뱀파이어집단이 몰려있다면 완벽할 것입니다. 그럼 작은 트리를 만들려면 어떻게 하면 될까요? 만들수있는 모든 경우를 다 조합해볼까요? 안타깝게도 이럴 경우 NP문제가 됩니다. NP문제는 일반적으로 별로라고 알려져있습니다.
최고의 테스트를 찾는 방법
그렇다면 최고의 테스트는 어떻게 찾을까요? 위 데이터베이스를 보면 우리는 각각 그림자, 마늘, 안색, 억양에 대해 뱀파이어인지 아닌지에 대해 테스트할 수 있습니다. 그럼 테스트하나씩 살펴보겠습니다.
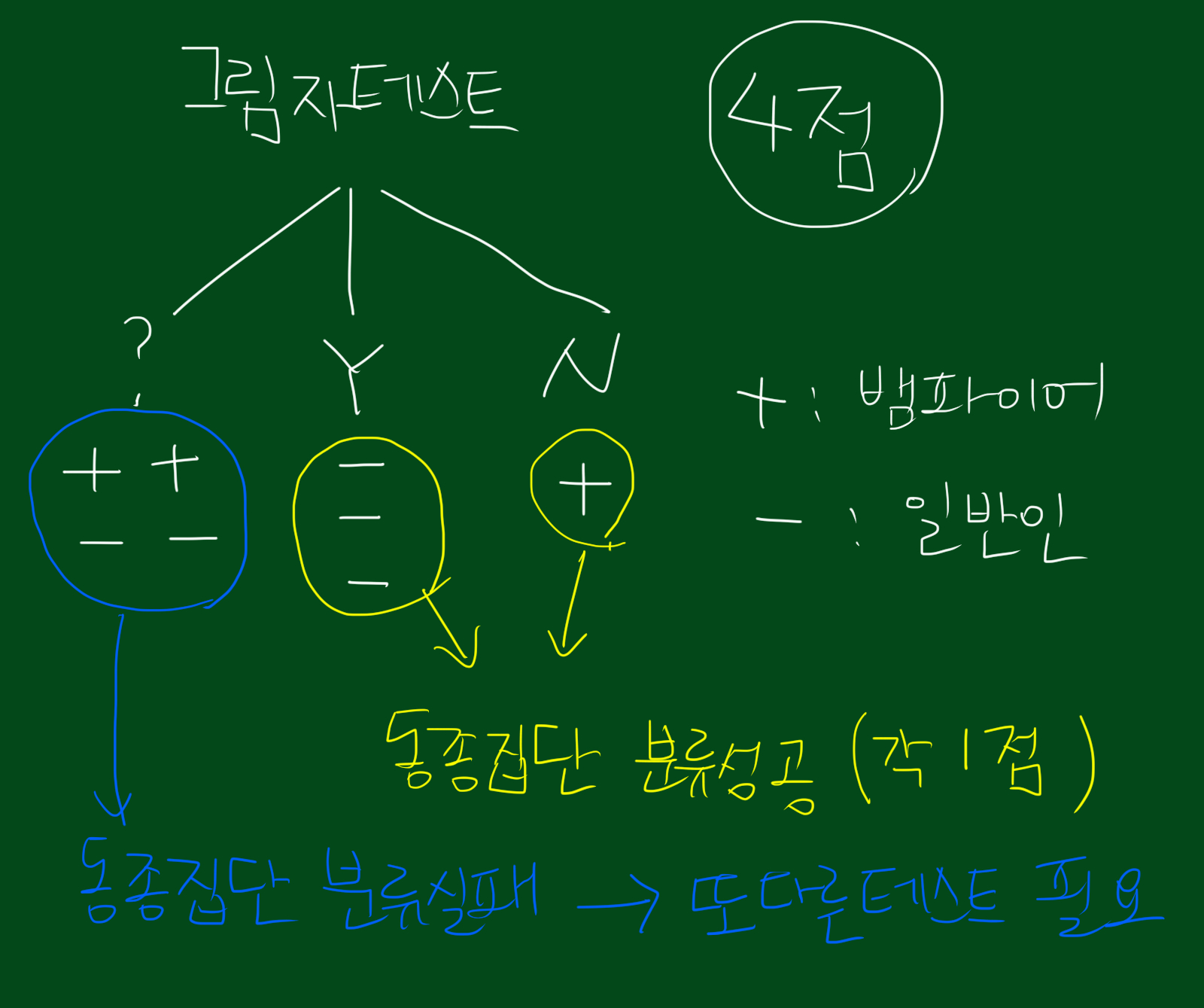
위 그림을 보시면 첫번째 그림자 테스트 입니다. 그림자 변수를 보고 뱀파이어인지 아닌지를 판단하는 테스트입니다. 보시면 Y의 경우 일반인을 정확히 검증하고, N는 완벽하게 뱀파이어임을 나타냅니다. 다만 ?인 경우에는 뱀파이어와 일반인이 섞여있네요. 즉, Y, N의 경우 동종집단으로 분리 가능하다는 뜻입니다. 이 테스트가 뱀파이어를 얼마나 잘 구분하냐고 점수를 매긴다면 4점이라고 할 수 있겠습니다. 음성 3명, 양성 1명을 맞춰서 3+1=4, 4점입니다. 위 테스트에서 ?인 경우에는 또다른 테스트가 필요하겠네요.
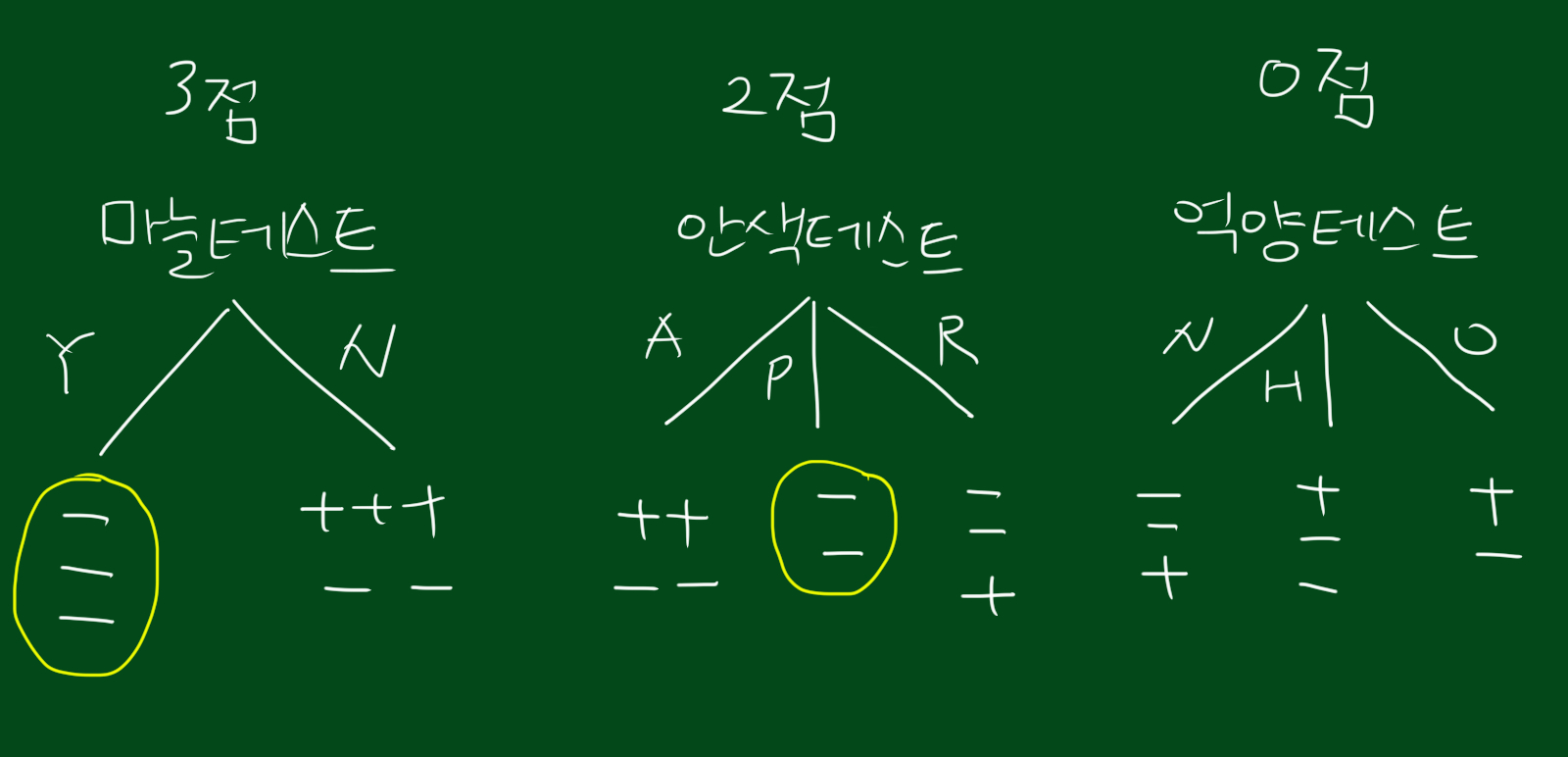
다른 세가지 테스트도 동일한 방법으로 점수를 매겨봅니다. 순서대로 마늘테스트(3점), 안색테스트(2점), 억양테스트(0점)입니다. 억양테스트는 하나도 구분할 수가 없네요ㅜ
그렇다면 위 네개 테스트 중 어느테스트가 가장 유용할까요? 위에서도 말했듯, 가장 좋은 테스트는 밑단을 동종집단으로 만드는 테스트를 원합니다. 따라서 성능측정이 필요한데요. 위와같은 방법으로 성능측정을 했습니다.
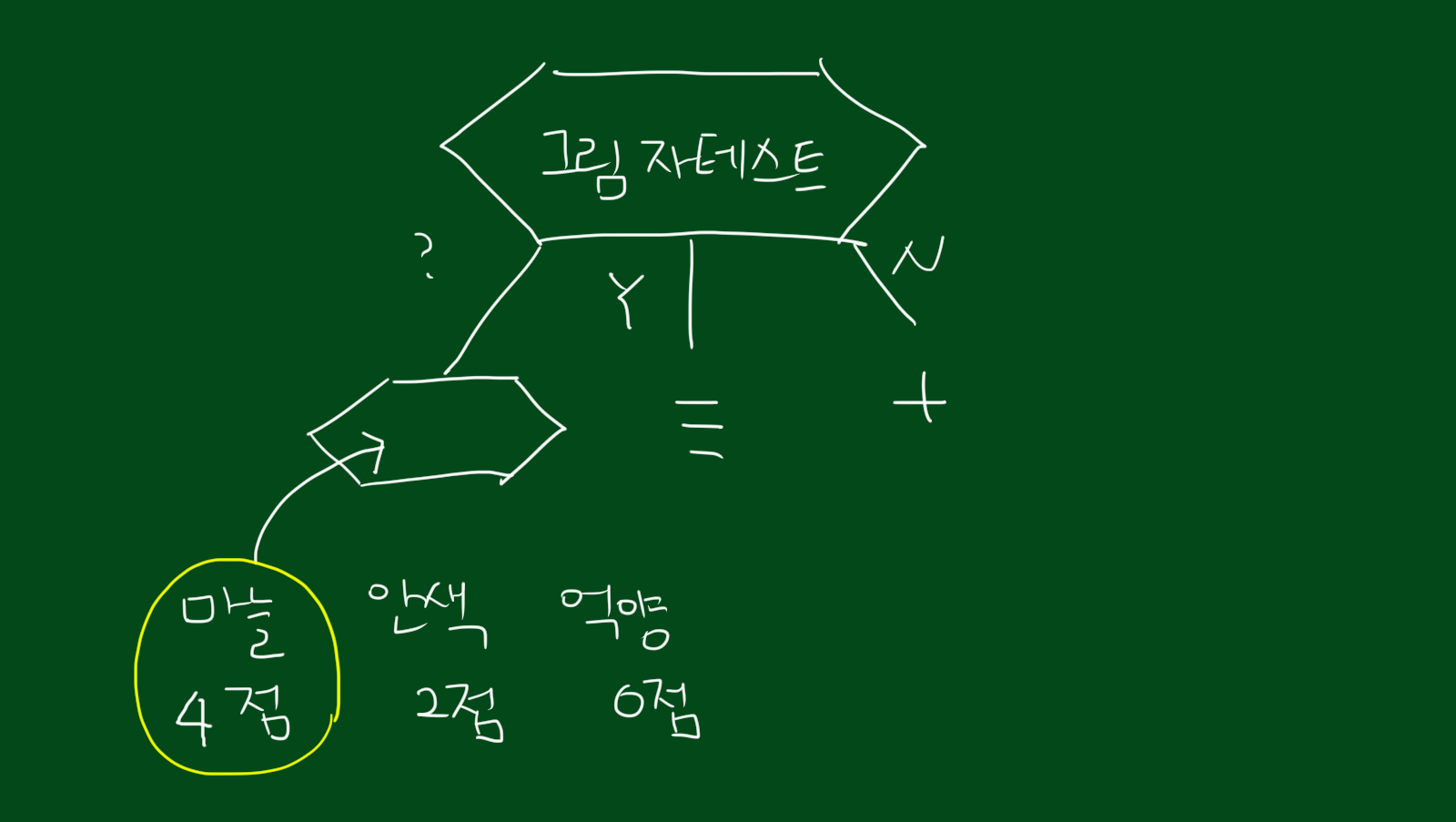
결국 위 점수를 토대로하면 가장 점수가 높은 그림자테스트를 우선 선발하고, 그림자테스트로 검증하지 못한 데이터에 대해서만 다시 테스트를 진행합니다.
즉, 위 그림처럼 기존에 존재하던 데이터에서 형광색으로 표시한, 그림자가 ?인 경우인 데이터 4개에 대해서만 다시 테스트를 진행합니다.
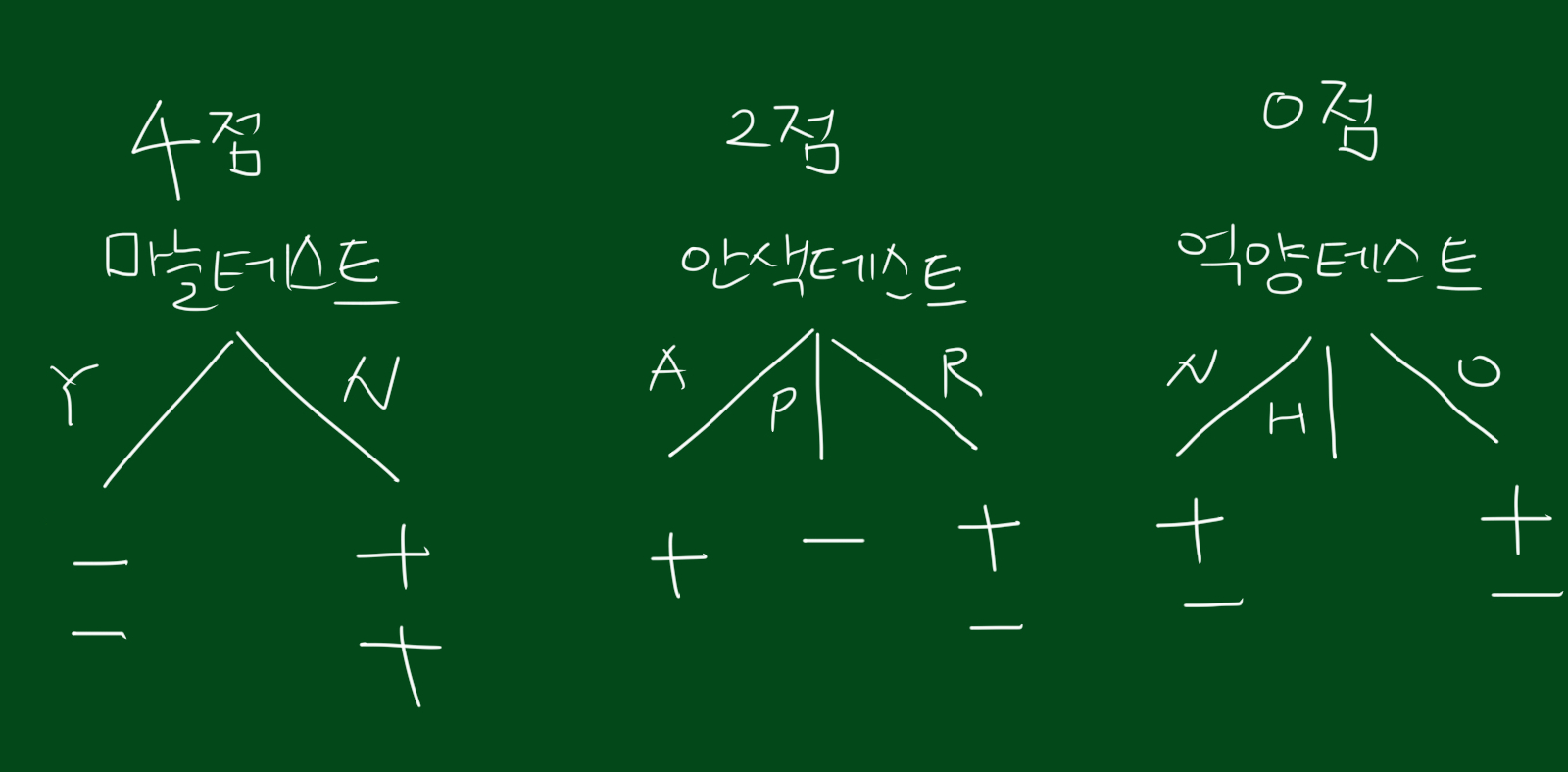
남은 4개의 데이터에 대한 테스트 결과는 위와 같습니다. 위 테스트 결과에서는 마늘테스트가 가장 뛰어나네요. 동종집단을 완벽히 갈랐습니다.

따라서 위와같이 마늘테스트가 두번째 테스트가 되는 것입니다.
빅데이터에 대해선 어떻게?
안타깝게도 위와 같은 테스트 방식은 빅데이터에 대해선 사용할 수 없습니다. 데이터가 크므로 하나의 테스트로 동종집단을 가르는 테스트는 아마 존재하지 않을 겁니다. 즉, 모든 테스트 점수가 0점이 됩니다. 따라서 이런 무질서 정도를 측정할 방법이 필요합니다. 참고로 무질서에 관한 것이라면 열역할자와 정보이론가(information theory)쪽이 잘 압니다.
무질서(disorder) 측정
정보이론가에 따르면 무질서 정도는 아래 공식을 구합니다. 무질서는 낮을 수록 좋습니다.
\[D(set) = -\frac{P}{T}\log_{2}\frac{P}{T}-\frac{N}{T}\log_{2}\frac{N}{T}\]이때, P는 positive, N은 negative, T는 전체숫자(P+N)을 의미합니다. 각 $\frac{P}{T}$에 대해 무질서 그래프를 그리면 아래와 같습니다.
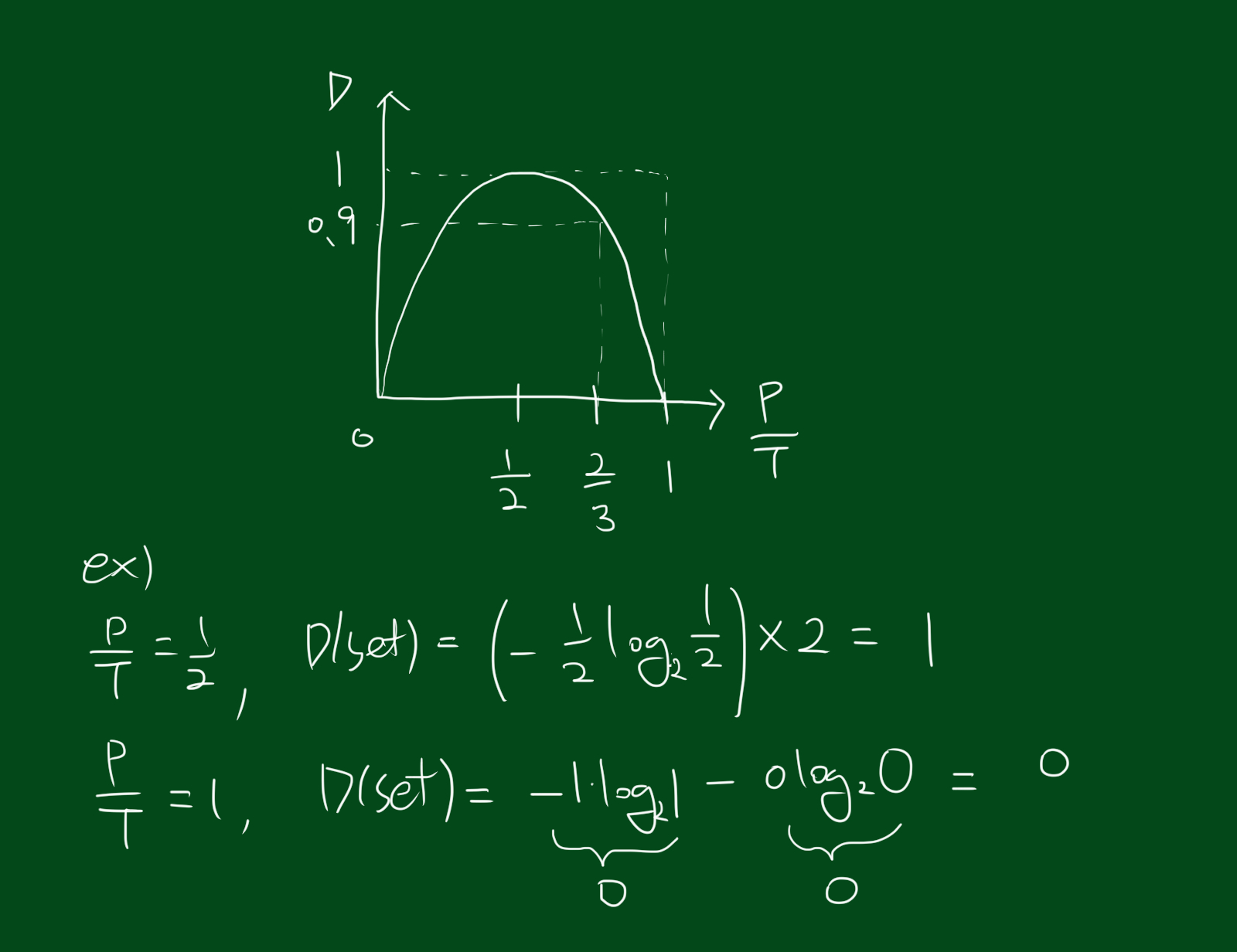
따라서 위 그래프의 특징을 잘 기억하고 있으면 일일이 계산하지 않고도 무질서정도를 계산하기 쉽습니다. 위 식은 테스트의 한 갈래에 대해서 무질서정도를 구한것이구요. 갈래들이 모인 테스트에 대해선 각 갈래에 대한 합이 필요합니다.
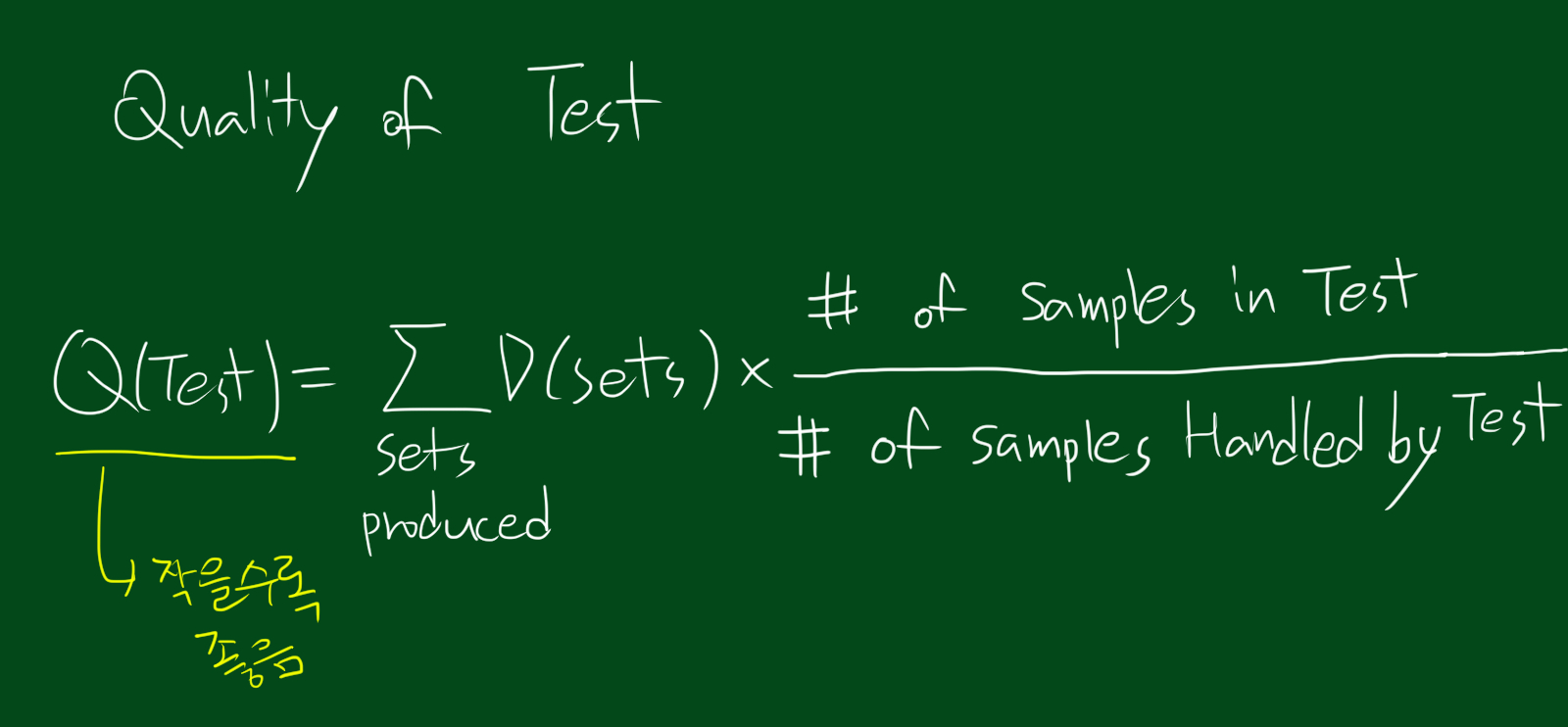
위 식처럼 하나의 테스트의 퀄리티는 각 갈래의 무질서 정도를 가중 합하는 것으로 구할 수 있습니다. 그럼 이 방법을 이용해 위에서 사용했던 예제의 무질서와 퀄리티를 측정해봅시다.
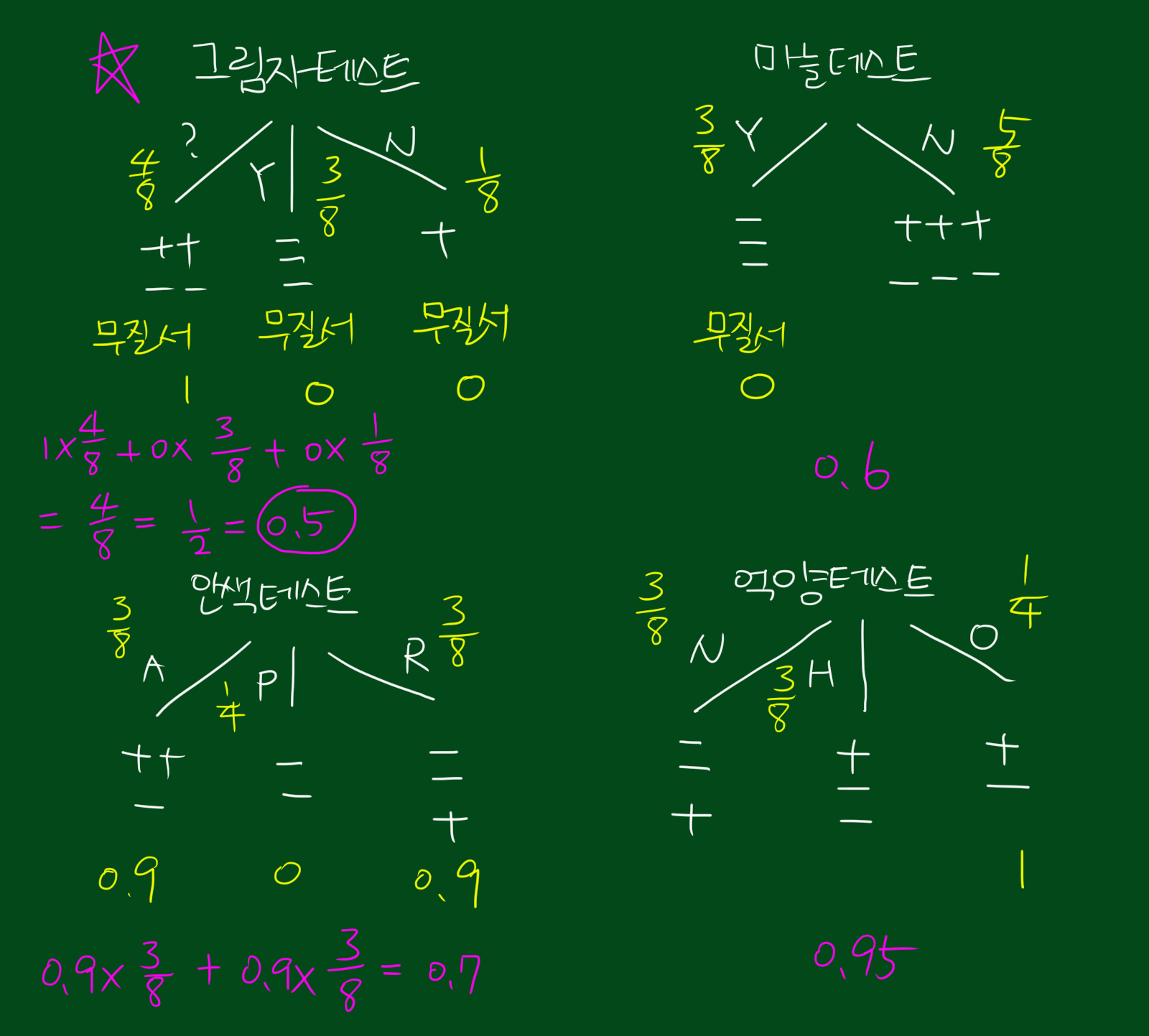
각 테스트에 대한 퀄리티를 구해보았습니다.
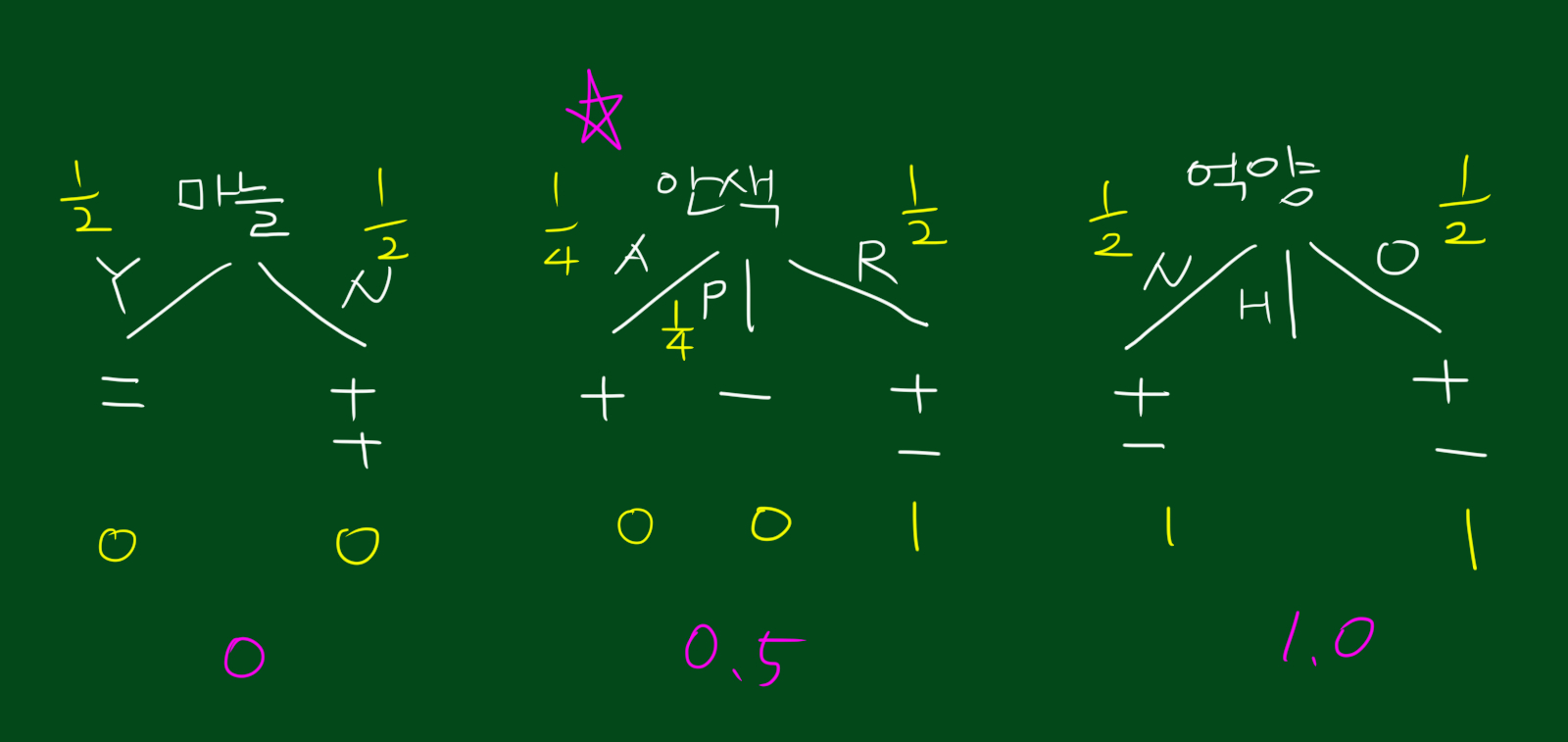
또한 두번째 테스트를 선발하기 위한 데이터에 대해서도 구했습니다. 위에서 쓴 결과와 동일하다는 것을 알 수 있죠. 이것이 의사결정나무에서 항상 쓰이는 winning mecanism입니다. 이 방법은 심지어 데이터가 숫자인 경우에도 사용할 수 있습니다. 아래 그림은 사람의 체온을 측정한 데이터입니다.
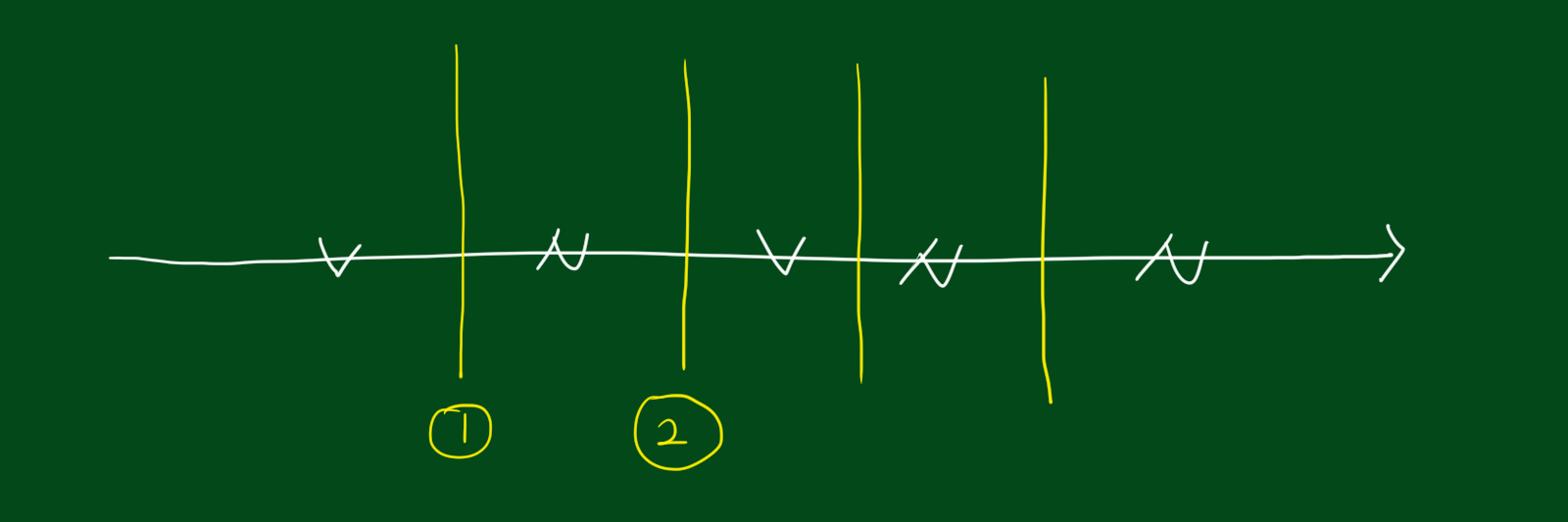
위 데이터를 테스트하기 위해서는 각 값들마다 사이값을 기준으로 테스트를 한번씩 다해보면 됩니다. 즉, 모든 값과 값 사이가 후보가 되고 모든 후보에 대해 계산을 한번씩 다해보는 것입니다. (n-1개의 임계값 후보)
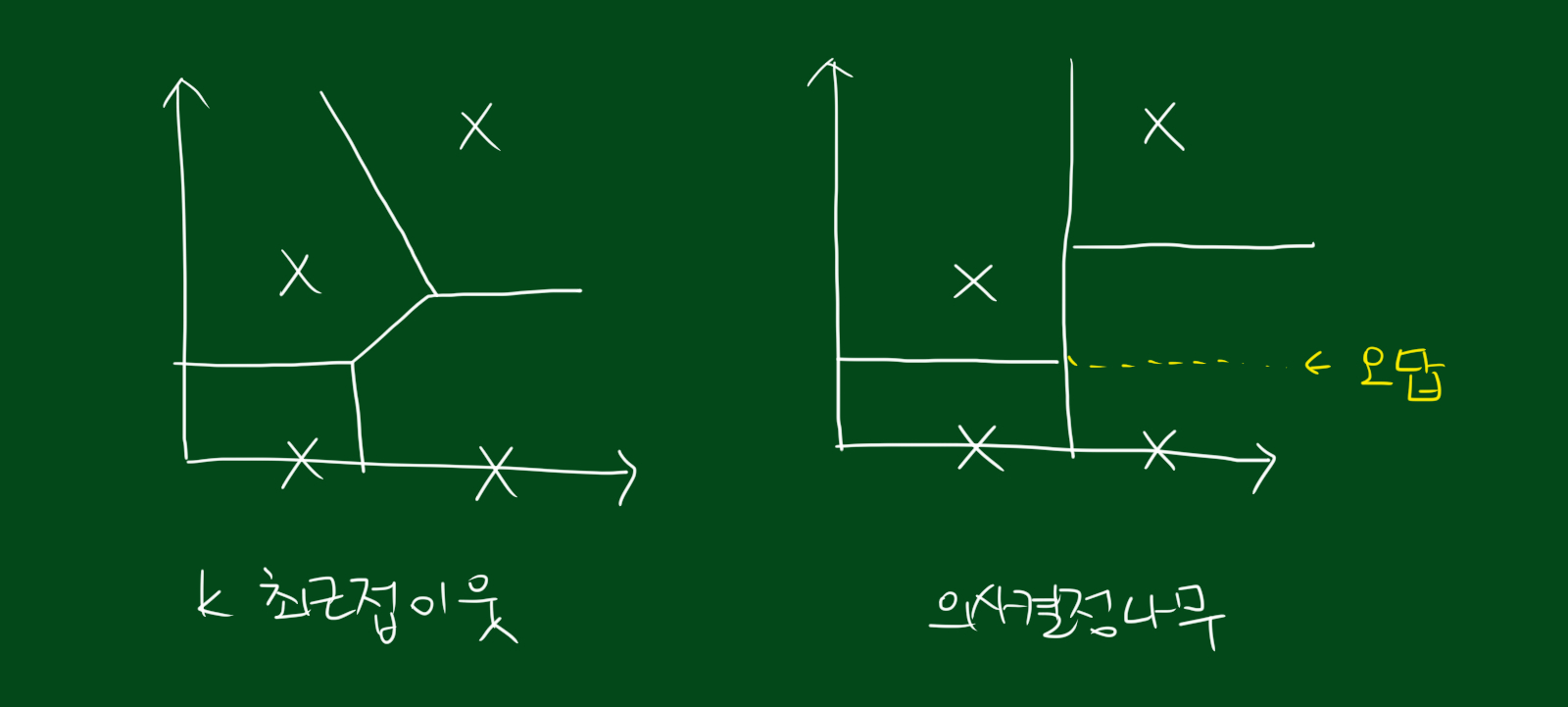
또한 k-최근접 이웃과는 다소 다른 분류그래프가 나타납니다.


