[딥러닝] 딥러닝 기초(3) 편미분을 이용한 신경망 학습
업데이트:
딥러닝 기초(3) 편미분을 이용한 신경망 학습
참고링크
편미분을 통해 알고 싶은 것
앞선 포스팅에서 우리는 임계치를 사용하는게 애매해서 t를 0으로 바꿈으로써 임계치를 없앴습니다. 또한 계단함수를 쓰는게 애매해서 계단함수 대신 시그모이드 함수를 사용하기로 했습니다. 자, 이제는 편미분값으로 신경망을 학습시킬수 있는지 알아보고 결과값을 우리가 원하는 상태로 정렬해봅시다. 참고로, 뉴런이 하나밖에 없으면 그것은 신경망이 아닙니다. 뉴런이 적어도 두개는 있어야 신경망이라고 할 수 있죠. 따라서 가장 간단한 형태의 신경망은 뉴런이 2개인 신경망입니다.
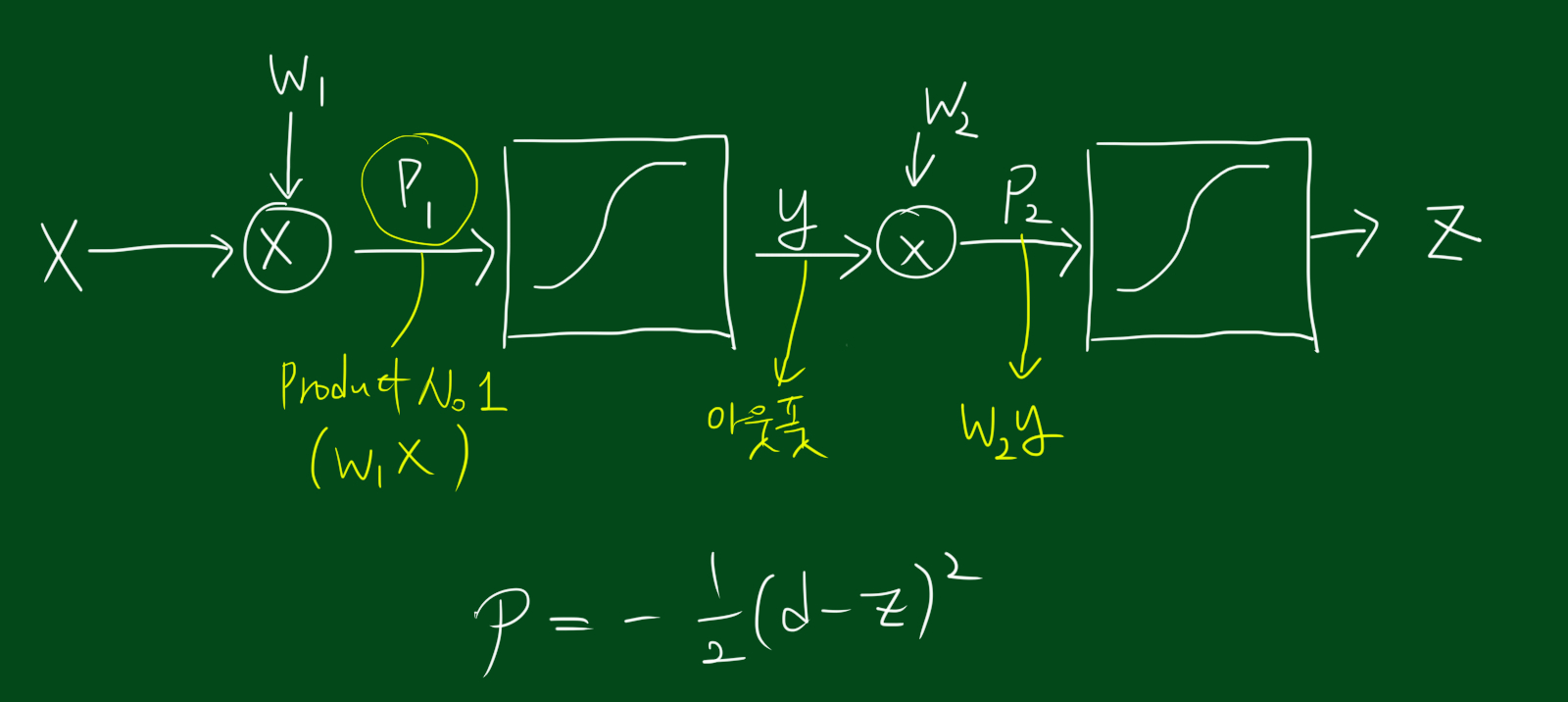
우리가 알고 싶은 것은 $w_2$를 움직였을 때 $z$가 얼마나 움직이는 지 알고 싶습니다. 그런데 자세히보니 $w_2$는 $z$로 가기전 중간에 $p_2$를 거칩니다. 결국 $w_2$에 대한 $z$의 변화율을 보기 위해서는 $p_2$를 움직였을 때 $z$가 얼마나 움직이는지, $w_2$를 움직일때 $p_2$가 얼마나 움직이는지 모두를 계산해서 곱해줘야합니다.(연쇄법칙) 자, 이제 연쇄법칙(chain rule)을 이용해 편미분을 다시 씁시다.
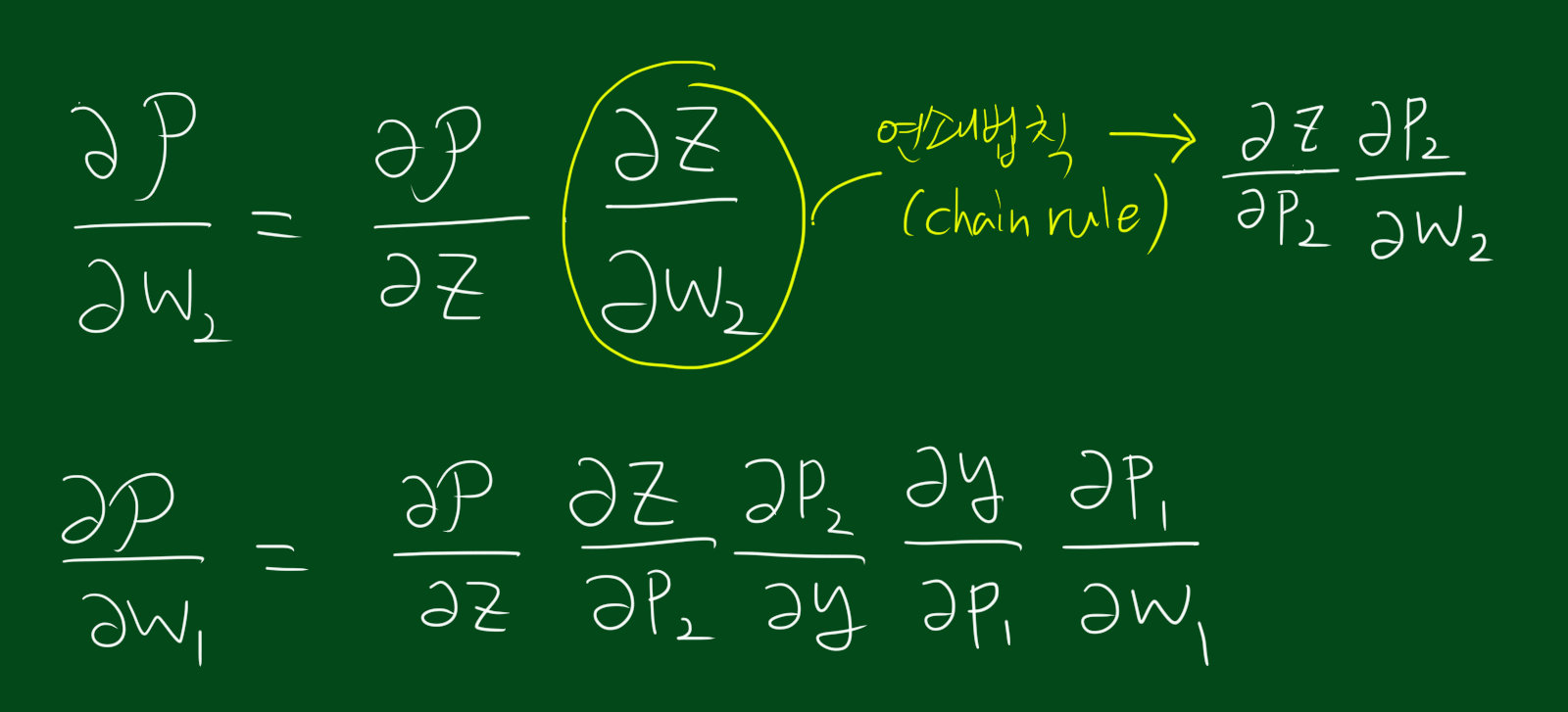
위 식을 보시면 $w_1, w_2$ 각각에 대한 성능함수의 변화율을 보실수 있습니다. 결과값을 얻기 위해 거치는 과정 모두를 적용시키기 위해 중간변수와 함께 연쇄법칙을 사용하였습니다.
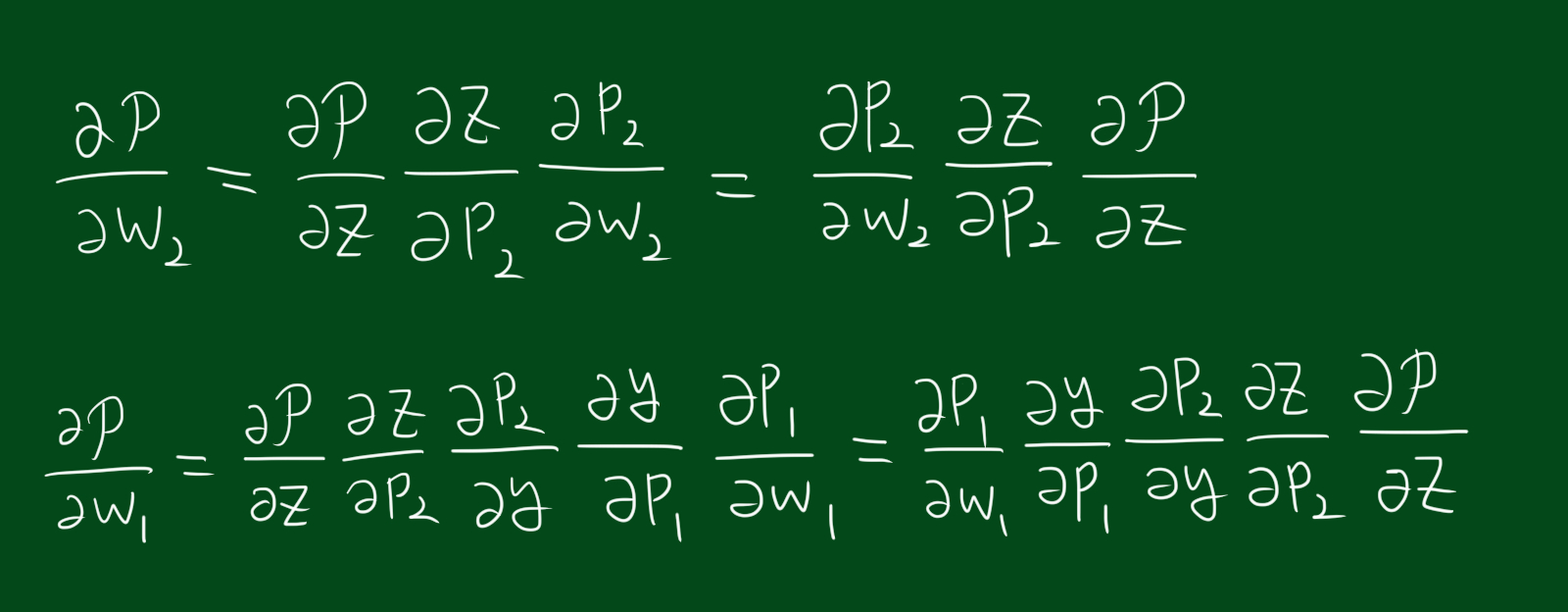
편의를 위해 식을 뒤집었습니다. 곱셈이므로 각 항의 위치를 서로 바꿔도 결과는 변함이 없습니다.
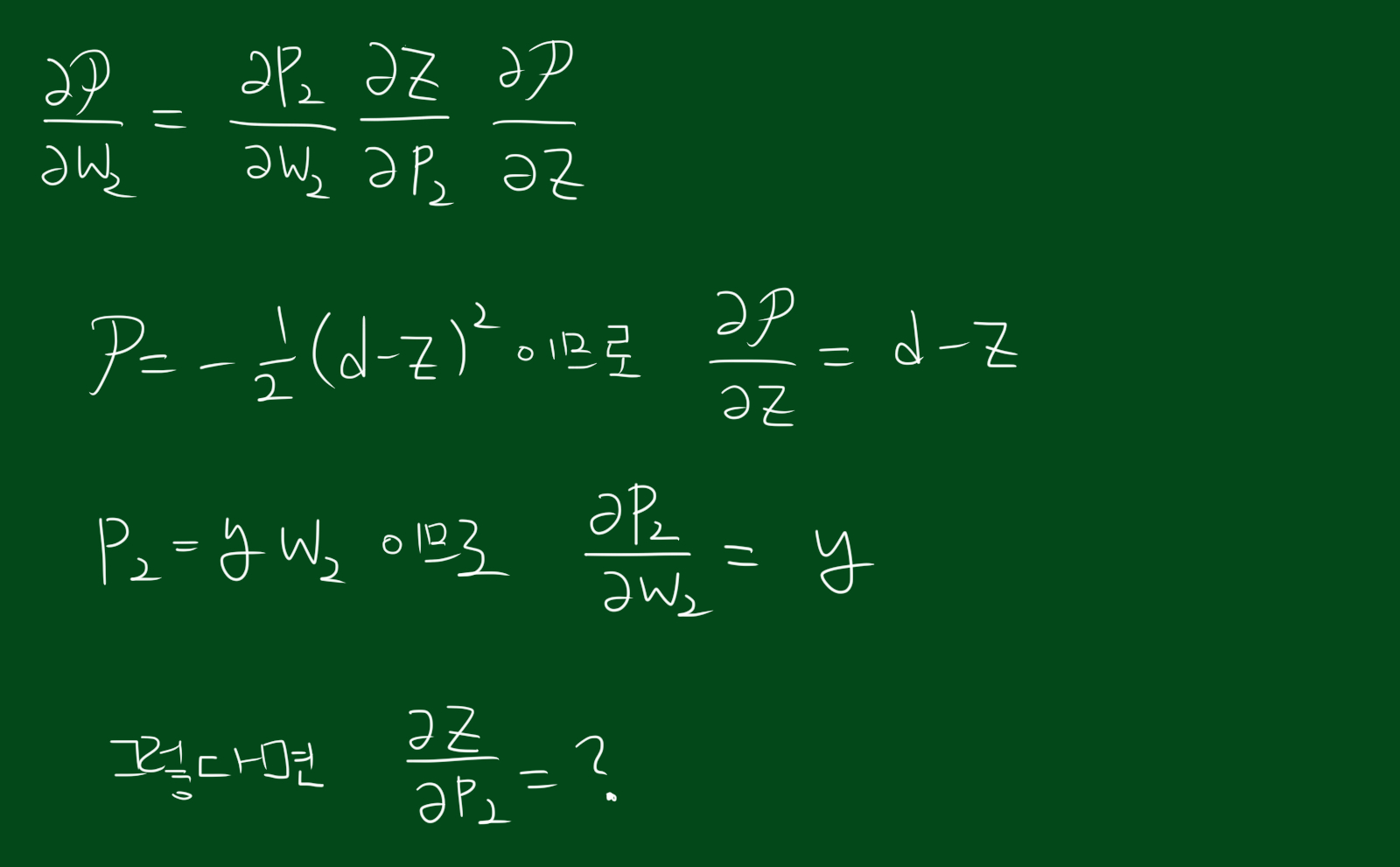
자, 이제 각 항을 편미분해보겠습니다. 위 그림처럼 앞선 두 항은 비교적 쉽게 계산을 했는데요. 마지막 세번째가 껄끄러울것 같습니다. 왜냐하면 $\frac{\partial z}{\partial p_2}$는 시그모이드 박스를 거치므로 정확한 값은 알 수 없습니다. 이 문제를 해결하려면 시그모이드 함수 내부의 $\alpha$ 에 대한 편미분 값을 알아야합니다.
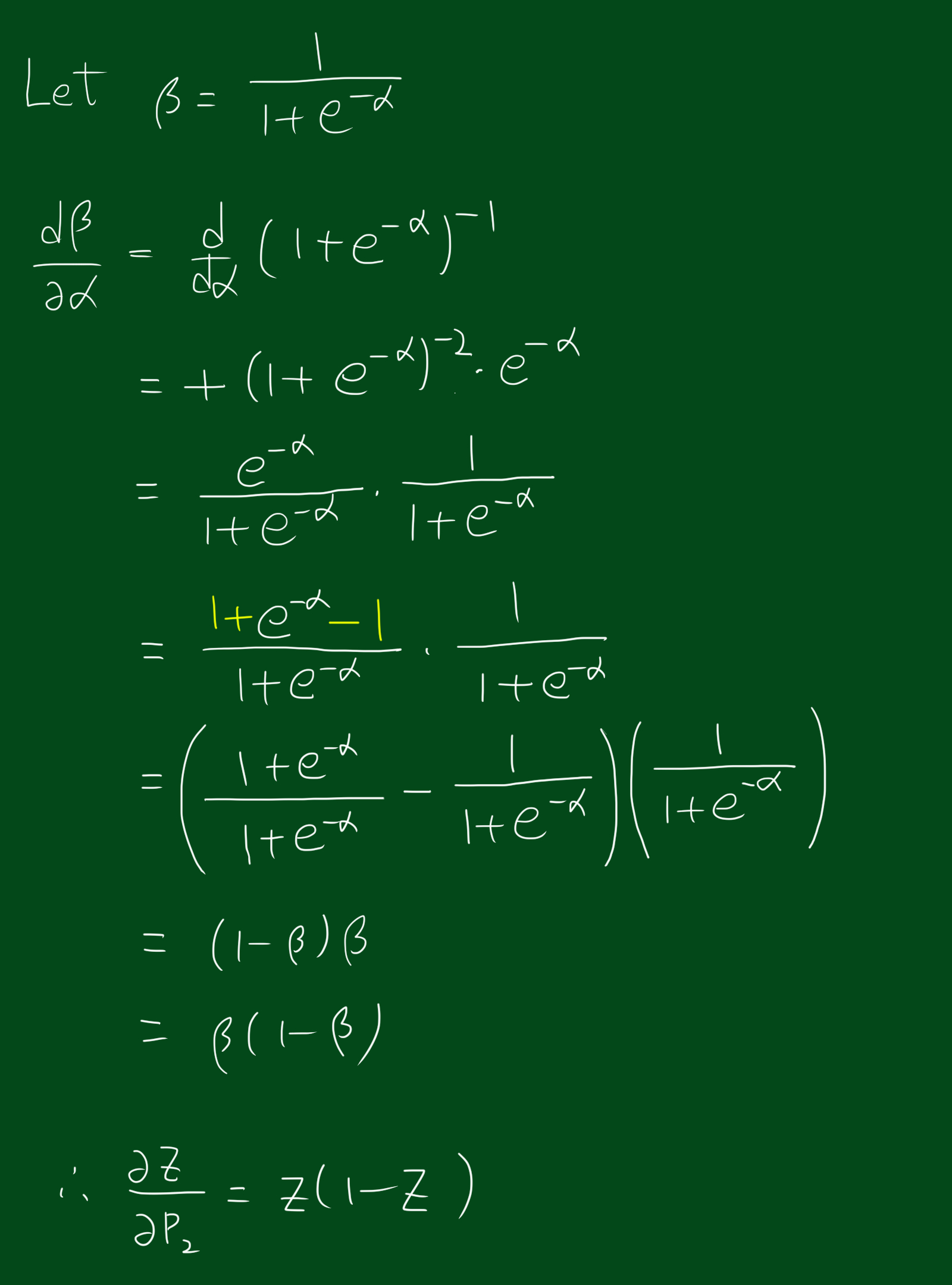
계산을 하고나니 신기한 형태가 나왔는데요.
잘보시면 입력값에 대한 출력값의 미분값은 출력값에 의해서만 결정됩니다! 즉, 시그모이드 함수 중 하나의 입력값에 대한 미분값을 보면 출력값 곱하기 $(1-\alpha)$를 하시면 됩니다.


