[딥러닝] 딥러닝 기초(4) 교차연결

딥러닝 기초(4) 교차연결

참고링크

머신러닝	딥러닝	선형대수	기초통계	최적화
k-means	신경망이란	고유값,고유벡터	확률변수	컨벡스 셋
k-최근접이웃	성능함수	행렬식	확률분포	컨벡스 함수
선형회귀	신경망 학습	내적	모집단과 표본	라그랑주 듀얼
로지스틱회귀	교차연결	기저	평균과 분산	KKT 조건
릿지,라쏘회귀	합성곱 신경망	랭크, 차원	공분산, 상관계수	ROC 커브
의사결정나무	배치, 에포크 차이	선형변환	최대가능도추정	크로스 밸리데이션
서포트벡터머신	텐서플로기초(1)	직교행렬	베르누이,이항분포	실루엣 스코어
원클래스 SVM	텐서플로기초(2)	고유값분해	기하,음이항분포
LDA	seq2seq	특이값분해	초기하분포
GMM	opencv기초		포아송분포
부스팅	resnet		정규분포
사이킷런 실습	다각형내부판별		감마분포
	엣지판별		지수분포
			카이제곱분포
			베타분포
			균일분포

교차연결

우리가 지금까지 다루었던 신경망은 아래와 같은 형태를 띕니다.

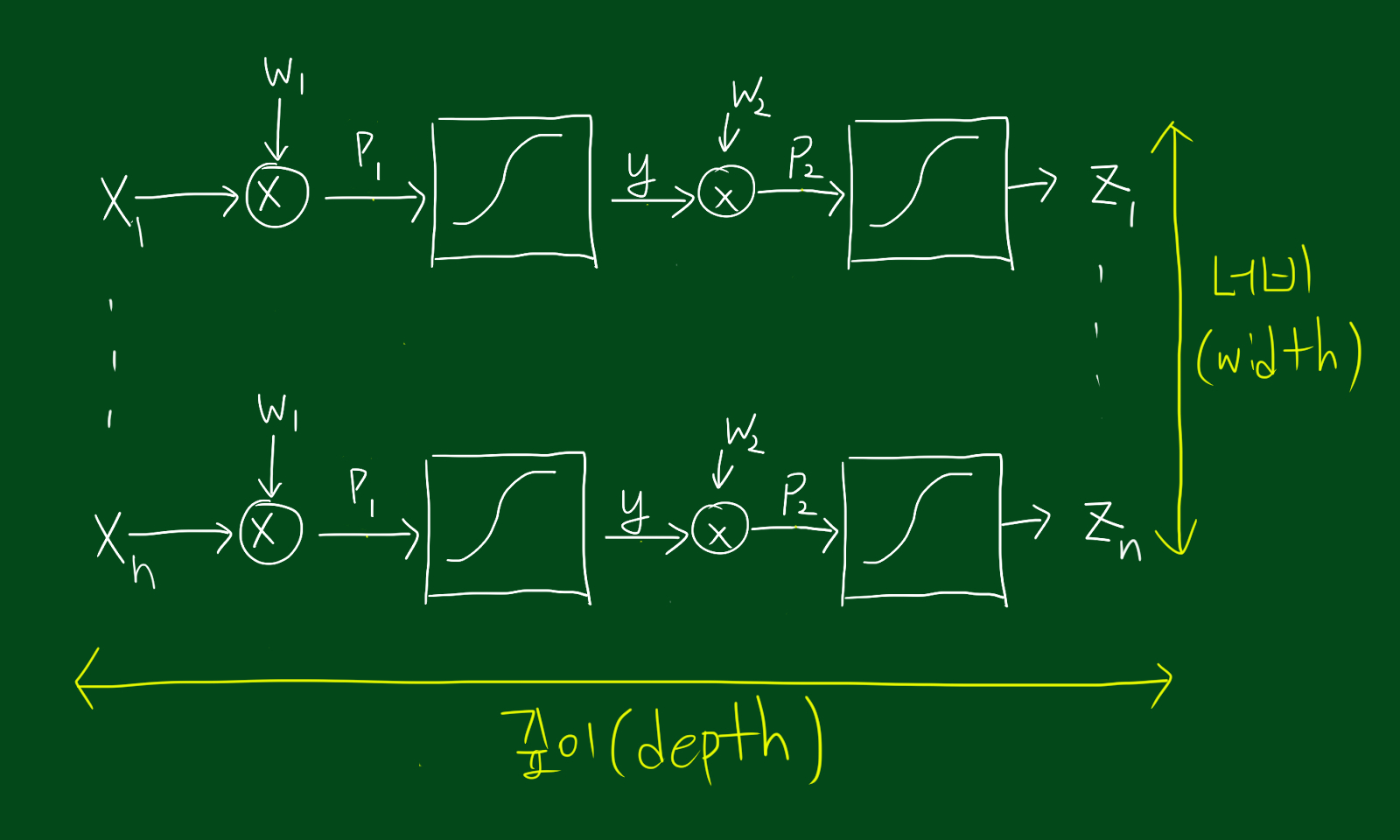
위 그림처럼 두 개의 입력값과 두 개의 출력이 있으면 성능함수에도 두 개의 숫자(두개의 목표값과 두개의 출력값을 이용)가 있을 것 입니다. 그렇다면 아래 그림 처럼 뉴런을 교차연결하면 어떨까요?

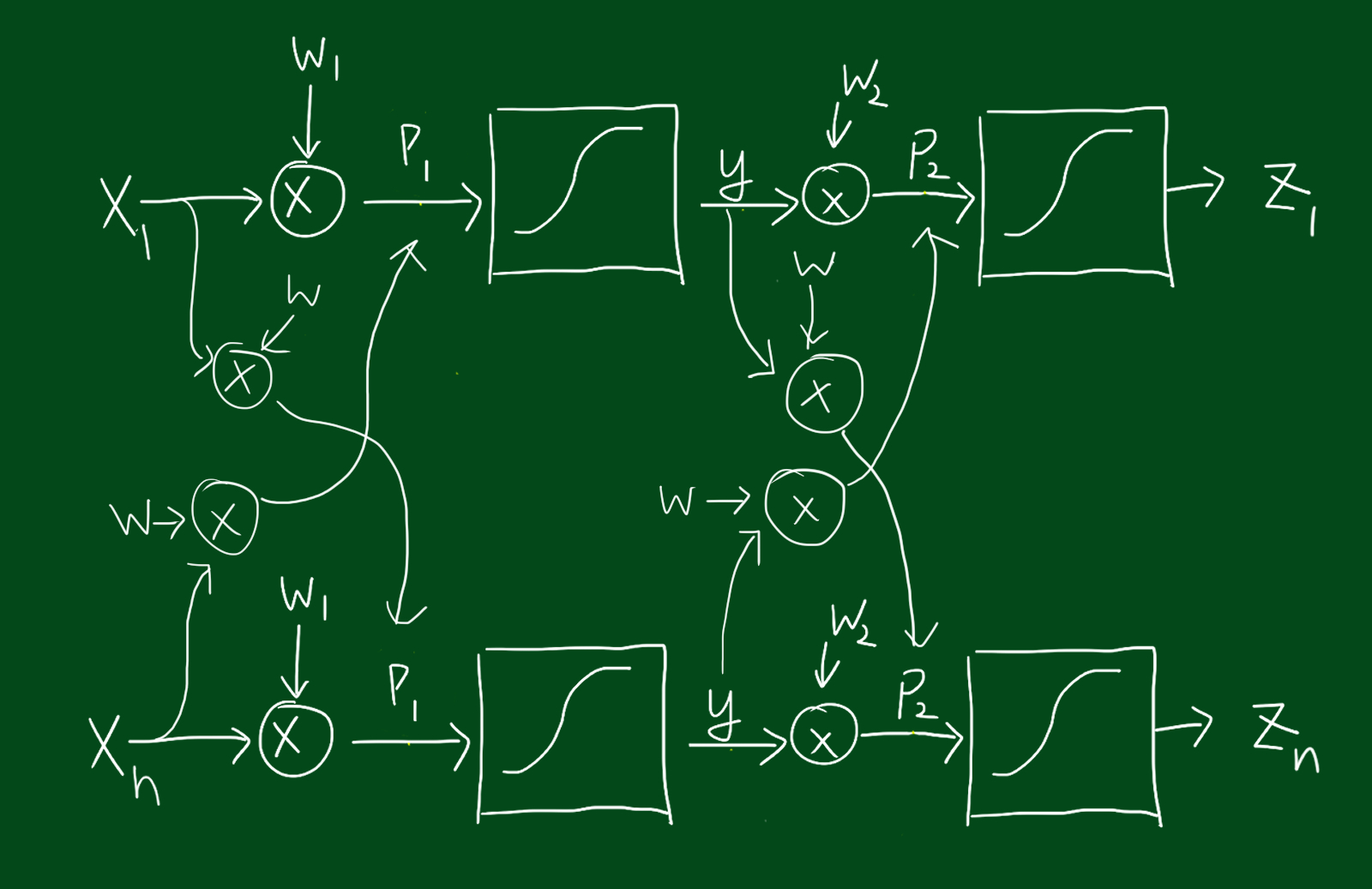
위 그림은 단지 두개의 뉴런을 교차연결했을 뿐인데도 인풋에서 아웃풋으로 가는 경로가 기하급수적으로 늘어났네요ㅜㅜ 그럼 학습을 위해 얼마나 많은 양의 편미분을 해야하는 것일까요ㅜㅜ

그런데 희소식이 있습니다. 위 식을 보시면 서로다른 편미분인데도 공통되는 부분이 발견됩니다. 즉 $w_1$에 대한 편미분을 위해 필요한 부분이 $w_2$에 대해 편미분할 때 이미 해 놓은 것입니다.

편미분 지옥?

그럼 이 관점에서 각 경우에 대해 미분을 계속하면 어떤 일이 생길까요? 생각해봅시다. 성능함수 $\mathcal{p} = -\frac{1}{2}(\vec{d}-\vec{z})^{2}$에 영향을 끼치려면 $p_2$를 반드시 거쳐야합니다. 이것은 네트워크의 깊이가 아닌 너비와 연관되어 있습니다. 즉, $p_2$와 아주 멀리 떨어진 변수 관련 값은 여러가지 연산 및 시그모이드 함수, 그리고 $p_2$를 거치면서 끝나게 됩니다. 그런데 위 단원에서 보시면 우리가 계산해야할 많은 부분이 이미 앞에서 많이 계산되었습니다. 따라서 생각만큼 계산량이 기하급수적으로 늘어나진 않습니다. 참고로 푸리에급수 또한 이렇게 기하급수적인 계산을 막기위해 앞서 계산한 결과를 다시 사용합니다.

계산량 요약

• 깊이가 늘어나면 계산량은 선형적으로 많아진다.(linear in depth)
• 너비에 대해선 연결의 갯수와 비례함(with respect to width, $w^2$)

경로별로 실제로 미분해 봅시다

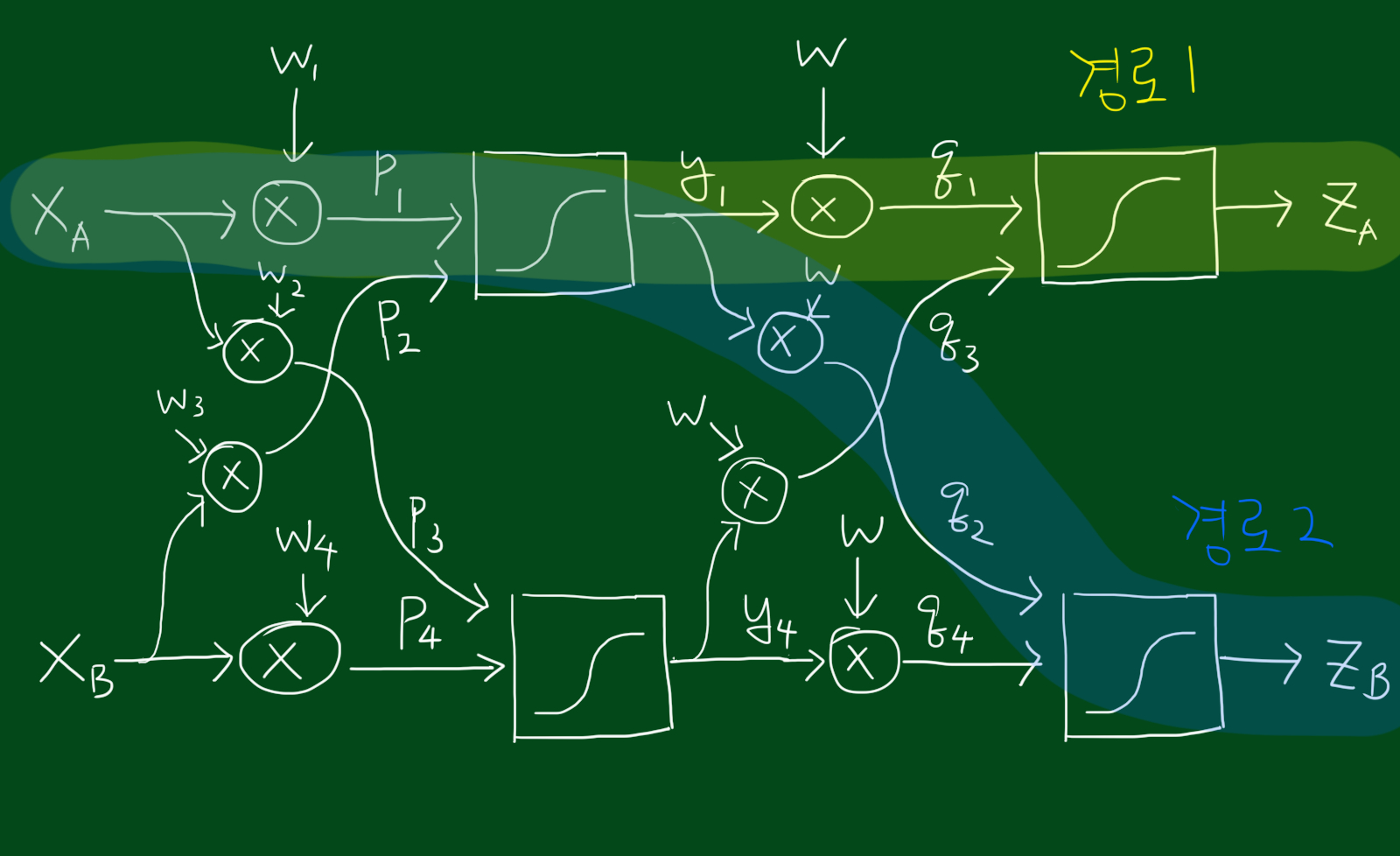
신경망에서 주목해야할 것은 행뿐만이 아니라 ‘열’도 중요합니다. 어떻게 출력값이 가중치에 영향을 받을까요. 경로1, 경로2에서 각각 $w_1$이 성능에 미치는 영향을 계산해보았습니다.

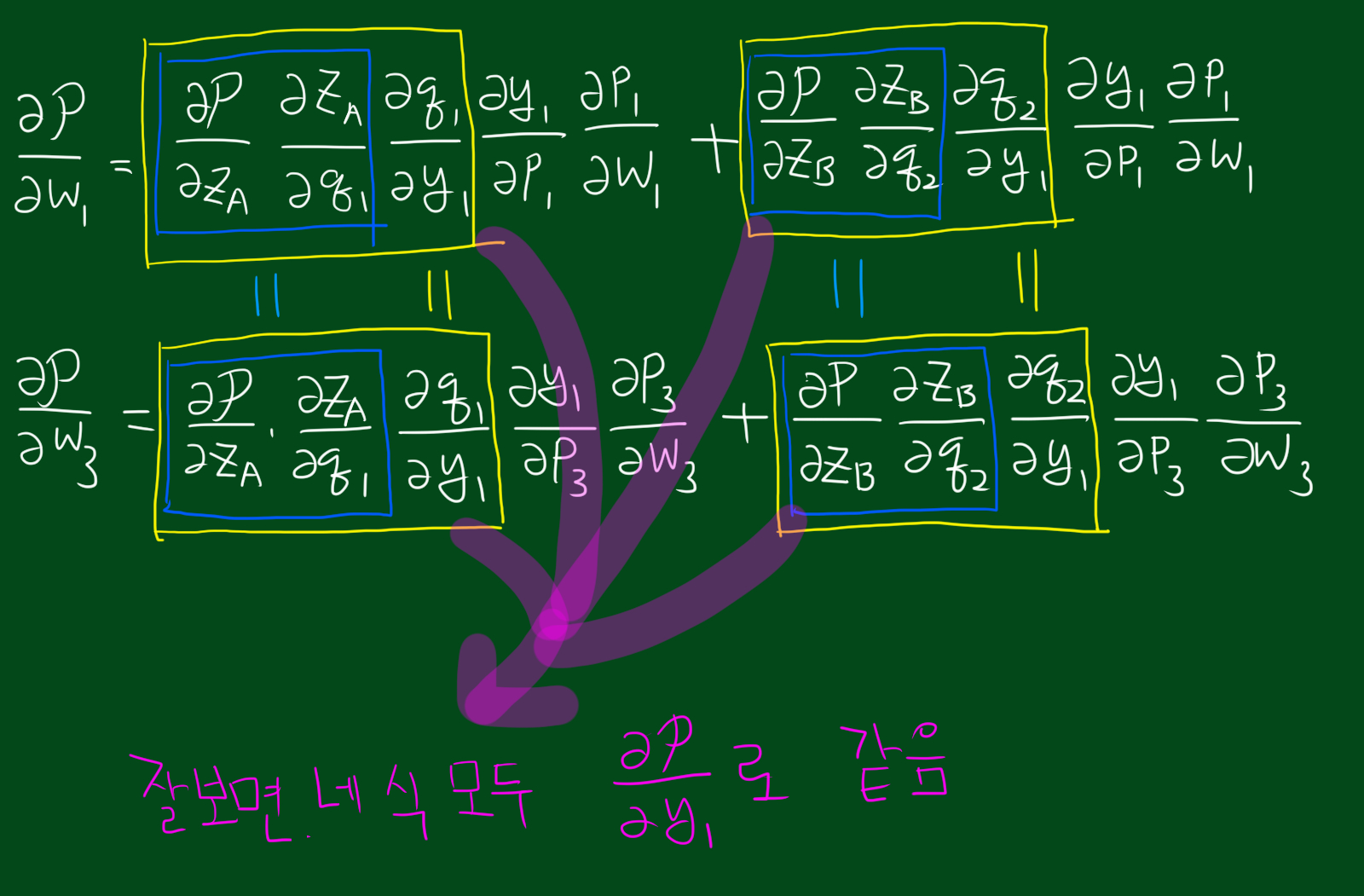
역시 위에서 언급했던데로 중복되는 계산이 존재하네요 ^^

5편으로 이동