[딥러닝] 딥러닝 기초(5) 합성곱(convolution) 신경망

딥러닝 기초(5) 합성곱(convolution) 신경망

참고링크

머신러닝	딥러닝	선형대수	기초통계	최적화
k-means	신경망이란	고유값,고유벡터	확률변수	컨벡스 셋
k-최근접이웃	성능함수	행렬식	확률분포	컨벡스 함수
선형회귀	신경망 학습	내적	모집단과 표본	라그랑주 듀얼
로지스틱회귀	교차연결	기저	평균과 분산	KKT 조건
릿지,라쏘회귀	합성곱 신경망	랭크, 차원	공분산, 상관계수	ROC 커브
의사결정나무	배치, 에포크 차이	선형변환	최대가능도추정	크로스 밸리데이션
서포트벡터머신	텐서플로기초(1)	직교행렬	베르누이,이항분포	실루엣 스코어
원클래스 SVM	텐서플로기초(2)	고유값분해	기하,음이항분포
LDA	seq2seq	특이값분해	초기하분포
GMM	opencv기초		포아송분포
부스팅	resnet		정규분포
사이킷런 실습	다각형내부판별		감마분포
	엣지판별		지수분포
			카이제곱분포
			베타분포
			균일분포

합성곱

사실 합성곱(convolution)이라는 단어는 신호와 시스템 쪽에서 나온 말인데요, 신호와 시스템에서 쓰이는 합성곱과 인공지능쪽에서 쓰이는 합성곱이라는 단어는 정확히 일치 하지는 않습니다. 왜냐하면 신호가 처리 될 때는 메모리를 포함하지 않기 때문입니다.

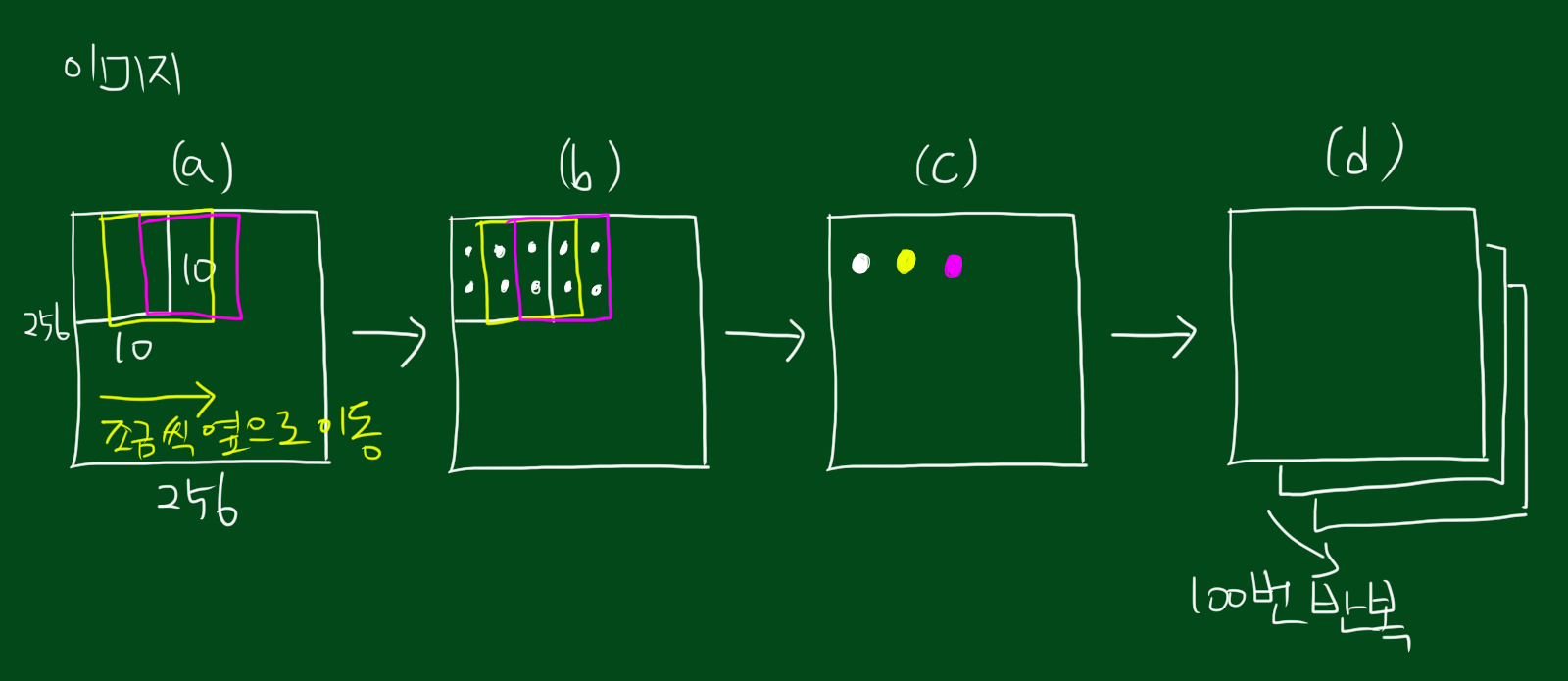
위 그림의 단계별로 설명하겠습니다.

(a) 그림은 256x256 이미지라고 생각하시면 되겠습니다. 이것을 학습시킬 때는 10x10 뉴런을 이용합니다. 즉 10x10 뉴런이 아웃풋을 생성합니다. 한번 실행한 이후로 옆으로 조금 움직여서(노란색) 또 실행하게 되고요. 그 다음에 또 조금 움직여서(분홍색) 실행하게 됩니다. 결국 뉴런의 배치가 각각 다른 출력값을 만들고 출력값은 이미지의 특정위치와 연관되어 있습니다. 이것이 합성곱(convolution)의 개념입니다.

(b) (a)의 합성곱을 통해 매우 많은 점이 생성됩니다. 이 점들을 가지고 무엇을 할 수 있을까요? 우리는 인접한 값들(local neighborhood)과 비교해 최대값을 찾을 것입니다.

(c) (b)에서 찾은 최대값을 가지고 이미지를 다시 매핑한 결과입니다. 이러한 과정을 풀링(pooling)이라고 하는데요. 이 경우에는 최대값을 사용하므로 max pooling이라고 부릅니다.

(d) (c) 다음에는 특정 뉴런을 가져와서 다른 이미지에 입힙니다. 이것을 커널(kernel)이라고 하는데요. 이 커널이라는 용어도 신호와 시스템에서 가져온 용어 입니다. 보통 하나의 커널로 100번 정도 반복하는데요. 다시 말하면, 우리는 256x256 이미지를 사용했고 10x10 커널을 이용했습니다.

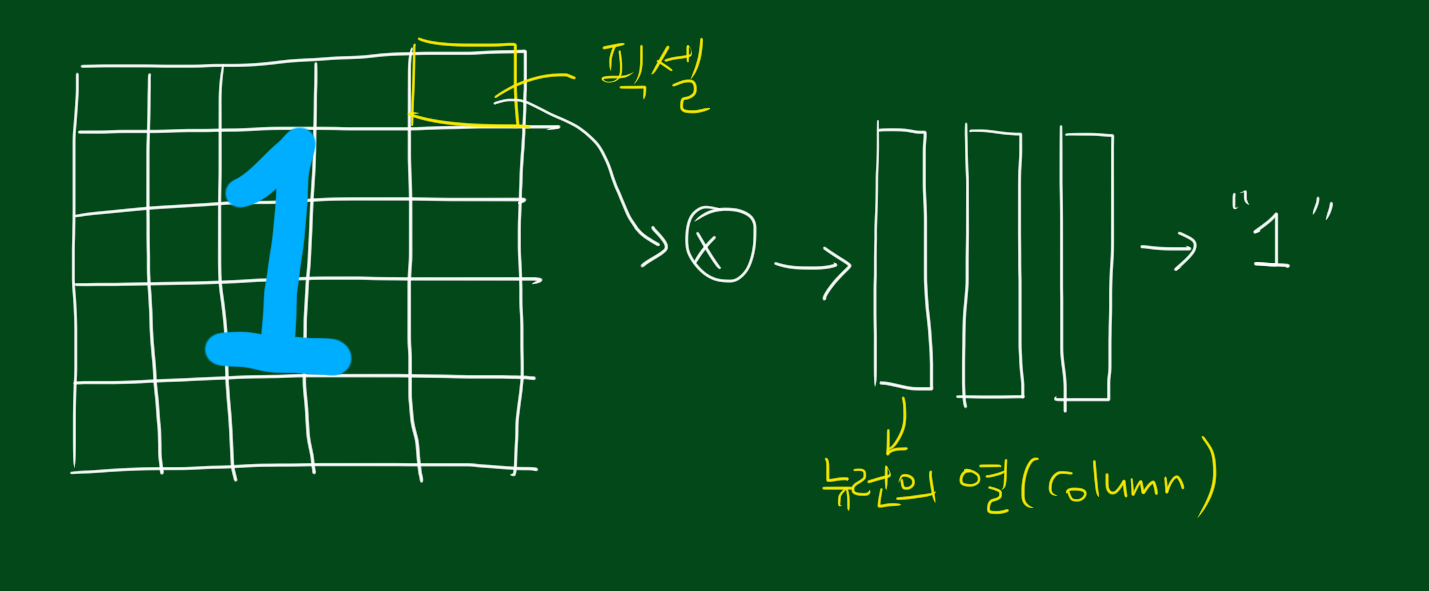
초기 딥러닝은 위 그림 처럼 다소 쉬운 신경망이었습니다. 위 그림에서 커널을 픽셀이라고도 하는데요. 이는 어떤 뉴런의 입력값이 될 수 있습니다. 딥러닝의 놀라운 점은 최종 결과가 함수근사자(function approximator)를 가진다는 것입니다. (그런데 왜 그런지는 아무도 모른다고 하네요 ㅠ) 여기까지 딥러닝의 기초 였습니다.