[최적화] 라그랑주 듀얼 함수(Lagrange dual function)의 개념

라그랑주 듀얼 함수(Lagrange dual function)의 개념

참고링크

머신러닝	딥러닝	선형대수	기초통계	최적화
k-means	신경망이란	고유값,고유벡터	확률변수	컨벡스 셋
k-최근접이웃	성능함수	행렬식	확률분포	컨벡스 함수
선형회귀	신경망 학습	내적	모집단과 표본	라그랑주 듀얼
로지스틱회귀	교차연결	기저	평균과 분산	KKT 조건
릿지,라쏘회귀	합성곱 신경망	랭크, 차원	공분산, 상관계수	ROC 커브
의사결정나무	배치, 에포크 차이	선형변환	최대가능도추정	크로스 밸리데이션
서포트벡터머신	텐서플로기초(1)	직교행렬	베르누이,이항분포	실루엣 스코어
원클래스 SVM	텐서플로기초(2)	고유값분해	기하,음이항분포
LDA	seq2seq	특이값분해	초기하분포
GMM	opencv기초		포아송분포
부스팅	resnet		정규분포
사이킷런 실습	다각형내부판별		감마분포
	엣지판별		지수분포
			카이제곱분포
			베타분포
			균일분포

최적화 문제의 표준 형식

최적화 문제의 표준적인 형식은 아래와 같습니다.

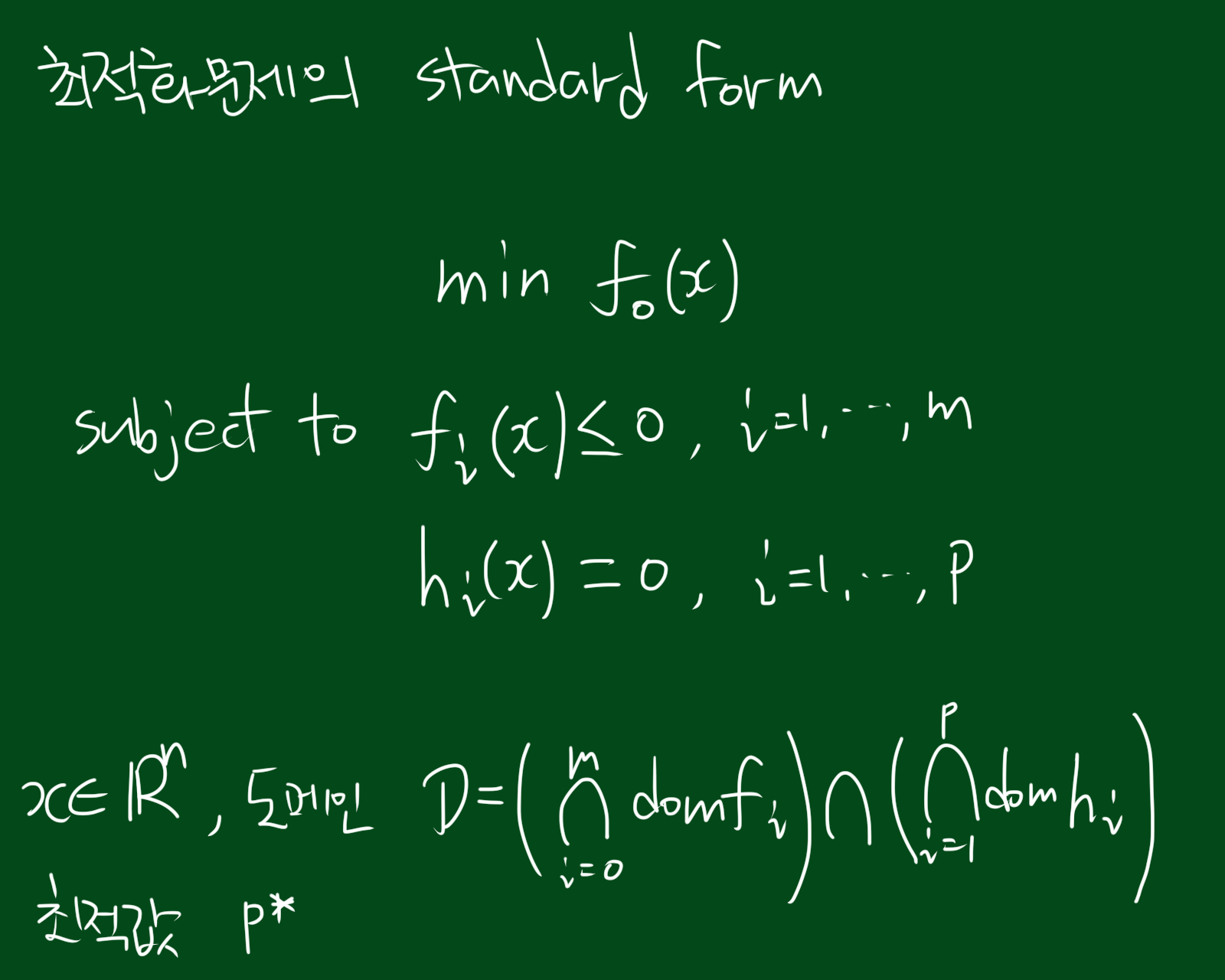
위 형식에서 $f_0(x)$를 우리가 최적화된 값을 구하고자 하는 목적함수(objective function)라고 하구요. subject to 다음 부터 나오는 부분, $f_i(x) \leq 0$, $h_i(x) = 0$을 제약식(constraint)라고 합니다. 위 최적화 문제는 목적함수와 제약식이 따로 분리되어 있는데요. 이를 하나의 식으로 정리한 것은 아래와 같으며, 아래와 같은 식을 라그랑주 프리멀 함수(Lagrange primal function)이라고 합니다.

라그랑주 프리멀 함수

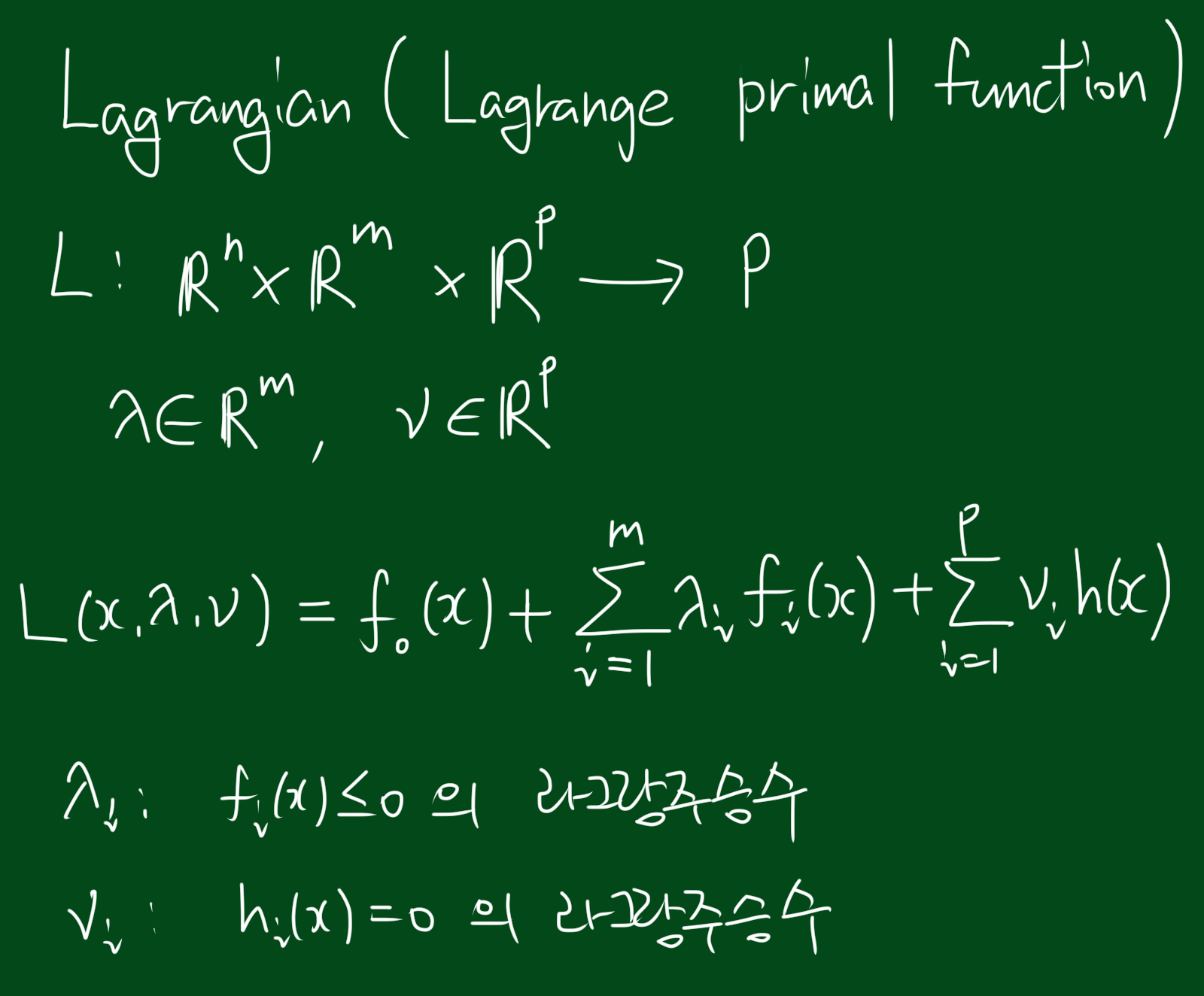
위 식에서 사용된 $\lambda_i$, $v_i$를 라그랑주 승수(Lagrange multiplier)라고 합니다.

라그랑주 승수 벡터

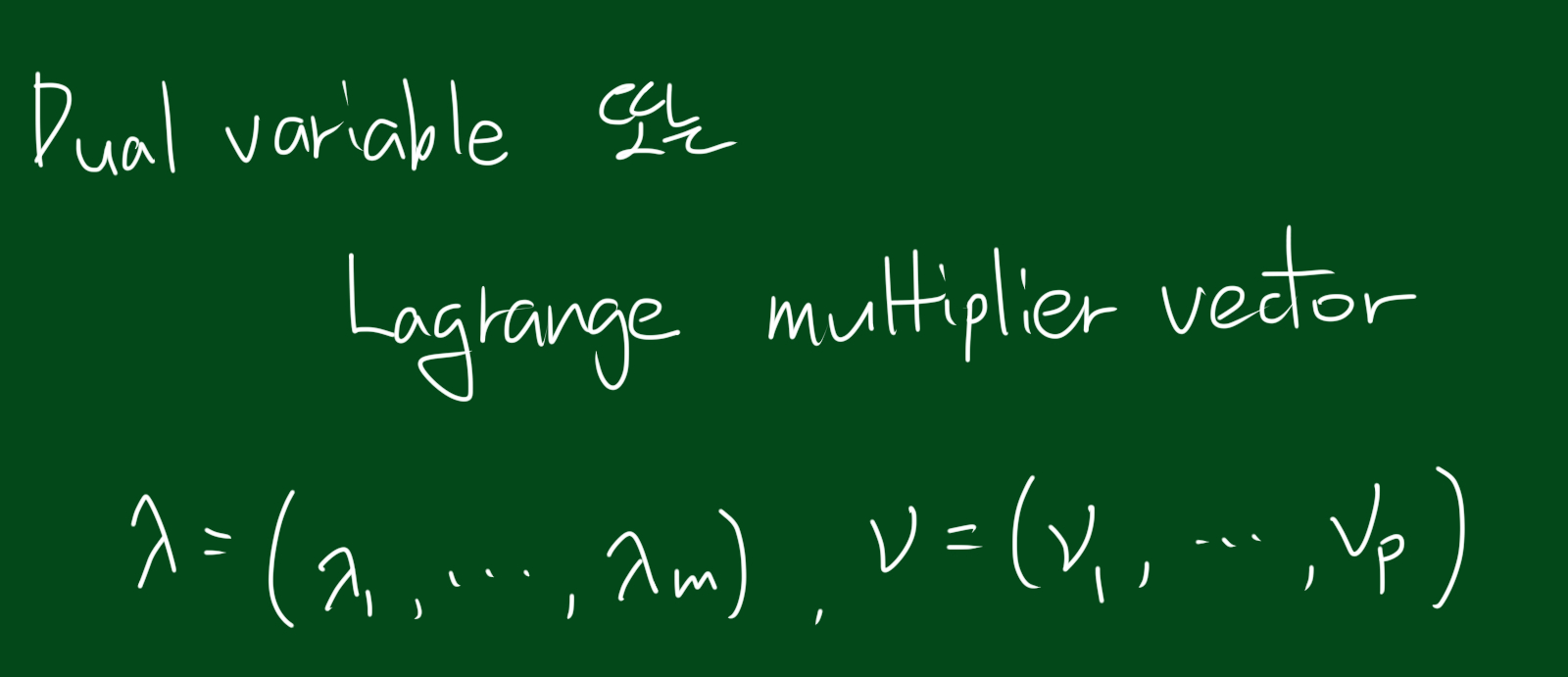
그리고 위와 같이 $\lambda_i$, $v_i$를 모아놓은 벡터를 라그랑주 승수 벡터(Lagrange multiplier vector)라고 합니다.

라그랑주 듀얼 함수

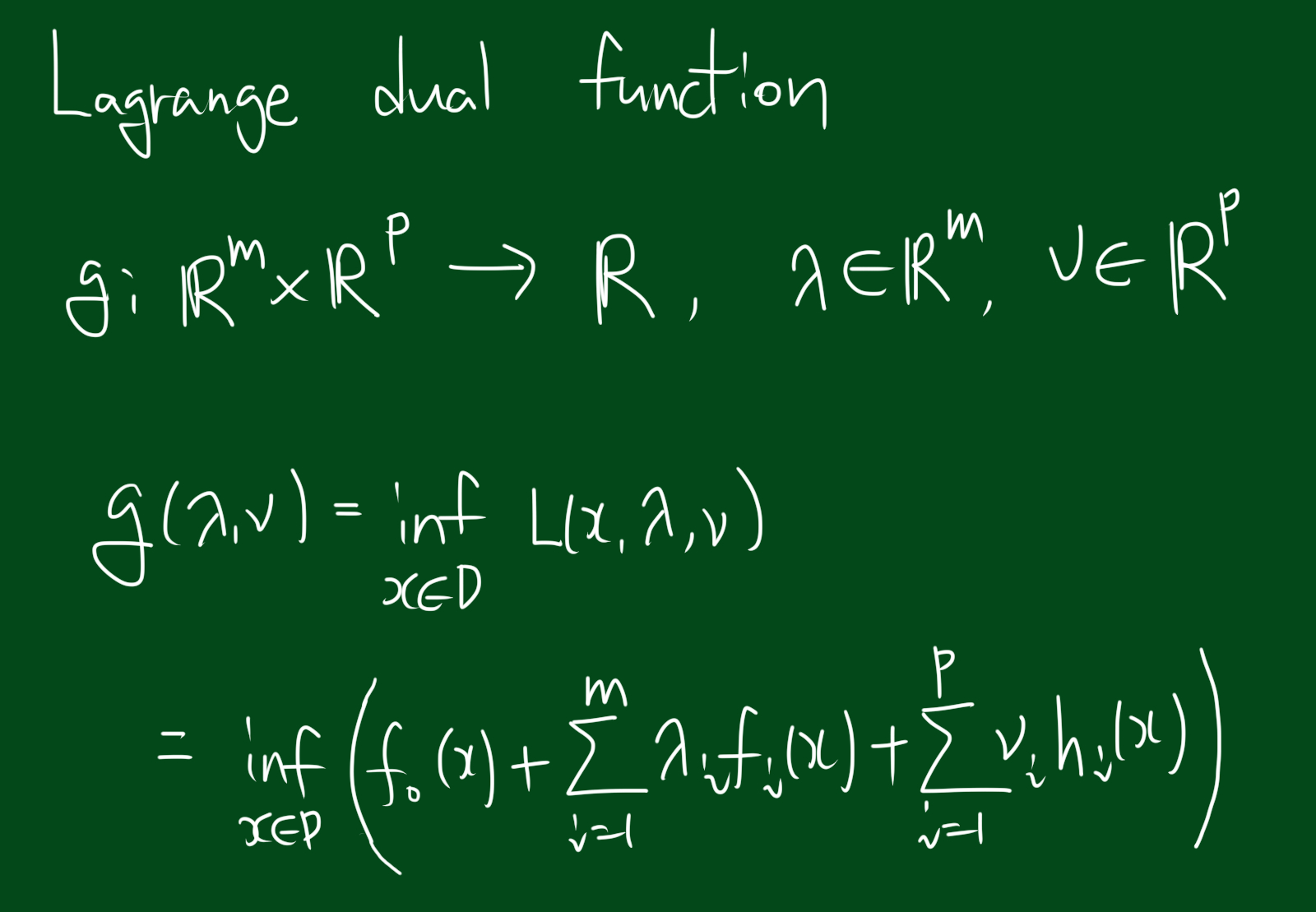
위와 같은 형태를 라그랑주 듀얼 함수(Lagrange dual function)이라고 하며, 라그랑주 프리멀 함수의 하한(infimum)을 나타냅니다. 만약 라그랑주 듀얼 함수의 최적값을 $d^{\ast}$라고 하고, 우리가 구하고자 하는 최적값을 $p^{\ast}$라고 하면 아래와 같은 부등식이 성립합니다.

\[d^{\ast} \leq p^{\ast}\]

위와 같은 성질을 weak duality라고 합니다. 또한 $p^{\ast} -d^{\ast}$를 optimal duality gap이라고 부릅니다. 이는 프리말 문제의 최적값인 $p^{\ast}$와 라그랑지 유얼 함수로부터 얻어진 lower bound $d^{\ast}$의 차이를 의미합니다. optimal duality gap은 nonnegative 합니다.

만약 아래와 같은 식을 만족한다면 strong duality라고 부릅니다.

\[d^{\ast} = p^{\ast}\]