[머신러닝] 릿지(ridge), 라쏘(lasso) 회귀분석 개념
업데이트:
릿지(ridge), 라쏘(lasso) 회귀분석 개념
참고링크
회귀분석 기초 복습
우리가 추정하고자 하는 모델을 아래와 같다고 하겠습니다.
$ y = f(z)+\epsilon, \, \, \, \epsilon ~(0, \sigma^2) $
그리고 우리가 만든 추정회귀함수를 아래와 같다고 하겠습니다.
$ \hat{f(x)} = z^T\hat{\beta} $
또한 최소제곱법(least squared)으로 구한 최소제곱 추정 모수를 $\hat{\beta}^{ls}$라고 하겠습니다. 이 때, 우리가 살펴봐야하는 점은
-
$\hat{\beta}$이 실제 $\beta$에 충분히 가까운가?
-
$\hat{f(x)}$이 미래 관측값에 대해 잘 피팅(fit) 되는가?
1번에 대해 우리는 아래와 같이 MSE(mean squared error)를 사용합니다.
$ MSE(\hat{\beta}) = E[\Vert \hat{\beta}-\beta \Vert^2] = E[(\hat{\beta}-\beta)^T(\hat{\beta}-\beta)] $
최소제곱법으로 구한 추정 모수에 대한 MSE를 구하면 아래와 같습니다.
$ E[(\hat{\beta}^{ls}-\beta)^T(\hat{\beta}^{ls}-\beta)] = \sigma^{2}tr[(Z^{T}Z)^{-1}] $
릿지(ridge) 회귀분석
제약이 없으면, $\beta_j$가 폭발(explode)적으로 커질수 있고, 이는 분산이 커지는 문제를 초래합니다. 따라서 이러한 문제를 막기위해 제약식을 사용하는데, 릿지 회귀분석(ridge regression)은 아래와 같은 제약식을 사용합니다.
$ minimize \sum_{i=1}^{n}(y_i - z_{i}^{T}\beta)^2 \, \, \, \, s.t. \sum_{j=1}^{p}\beta_{j}^{2} \leq t $
이는 아래와 같이 표현할 수도 있습니다.
$ minimize (y-Z\beta)^T(y-Z\beta), \, \, \, s.t. \sum_{j=1}^{p}\beta_{j}^{2} \leq t $
위에서, Z는 표준화(평균 0, 분산1)되었으며, y는 centered(평균값을 뺀) 되었습니다.
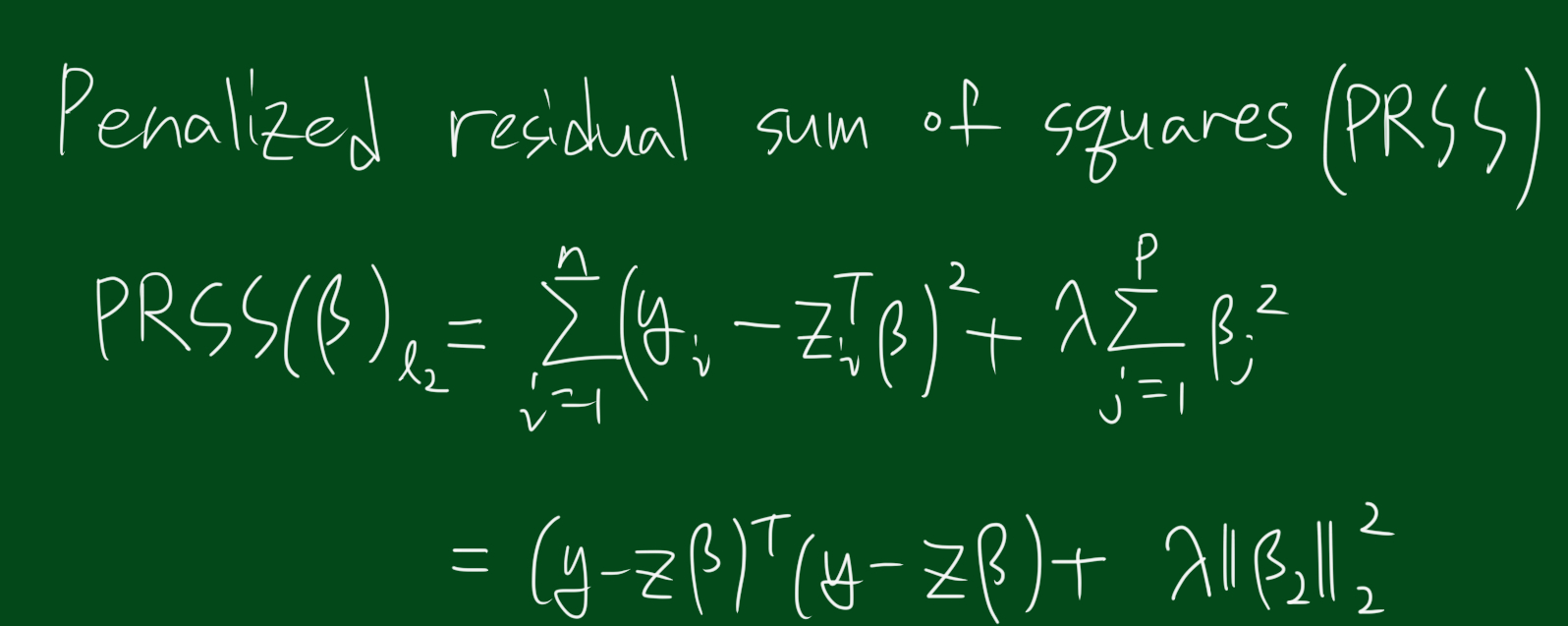
이는 컨벡스이며, 따라서 unique한 해를 가집니다.
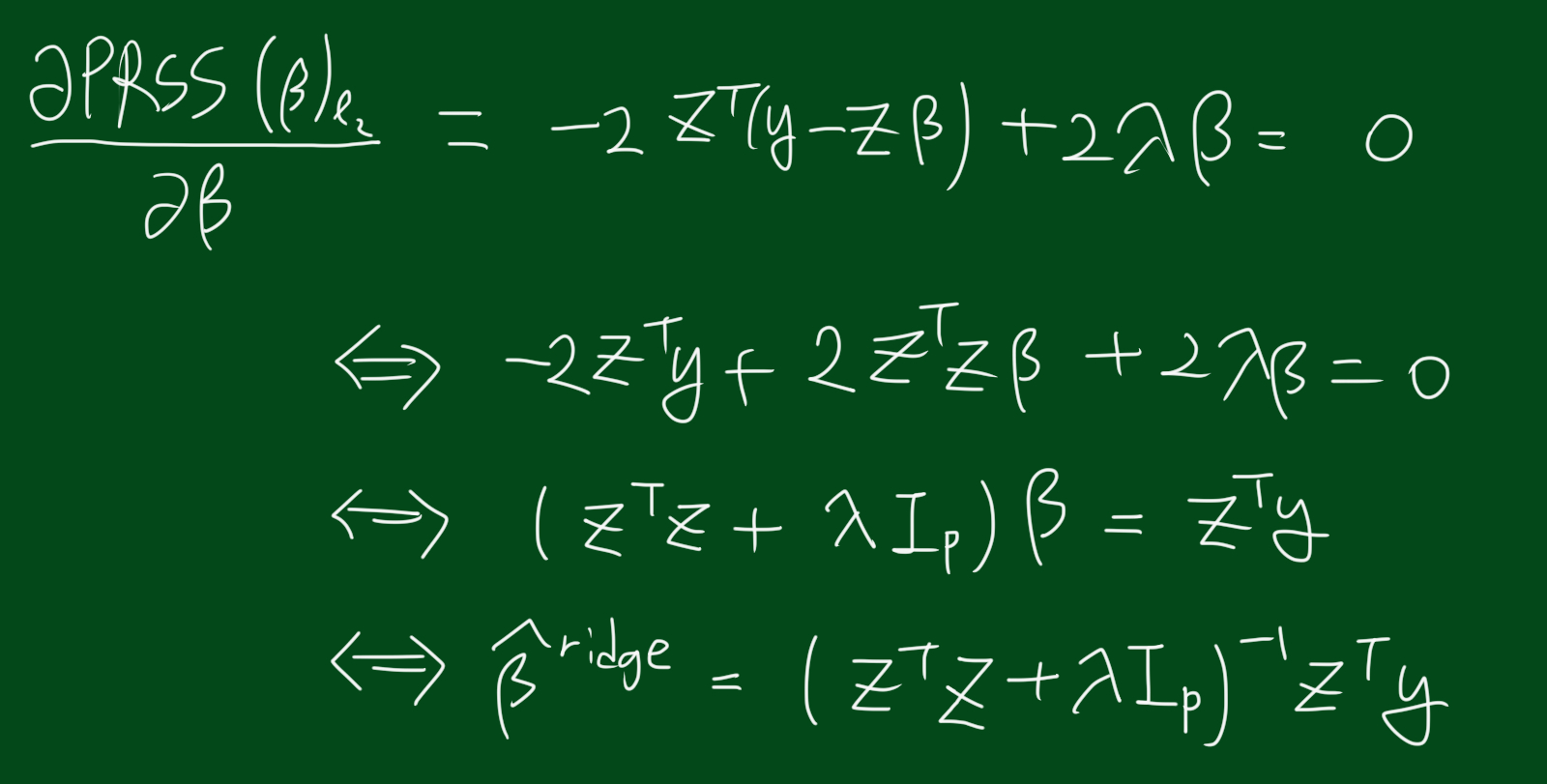
위 식에서 람다는 non-singular 문제로 만들어줍니다. 심지어 $Z^T Z$가 invertible이 아닐지라도 말입니다.
우리는 각각의 람다에 대해 해를 구할 수 있습니다. 람다는 shrinkage parameter 이며,
- $\lambda$는 계수(coefficient)의 사이즈를 조절합니다.
- $\lambda$는 정규식의 양을 조절합니다.
- $\lambda$가 0에 가까워질수록, 최소제곱추정량에 가까워집니다.
- $\lambda$가 무한대에 가까워질수록 $\hat{\beta}^{ridge}$는 0에 가까워집니다.(intercept-only model)
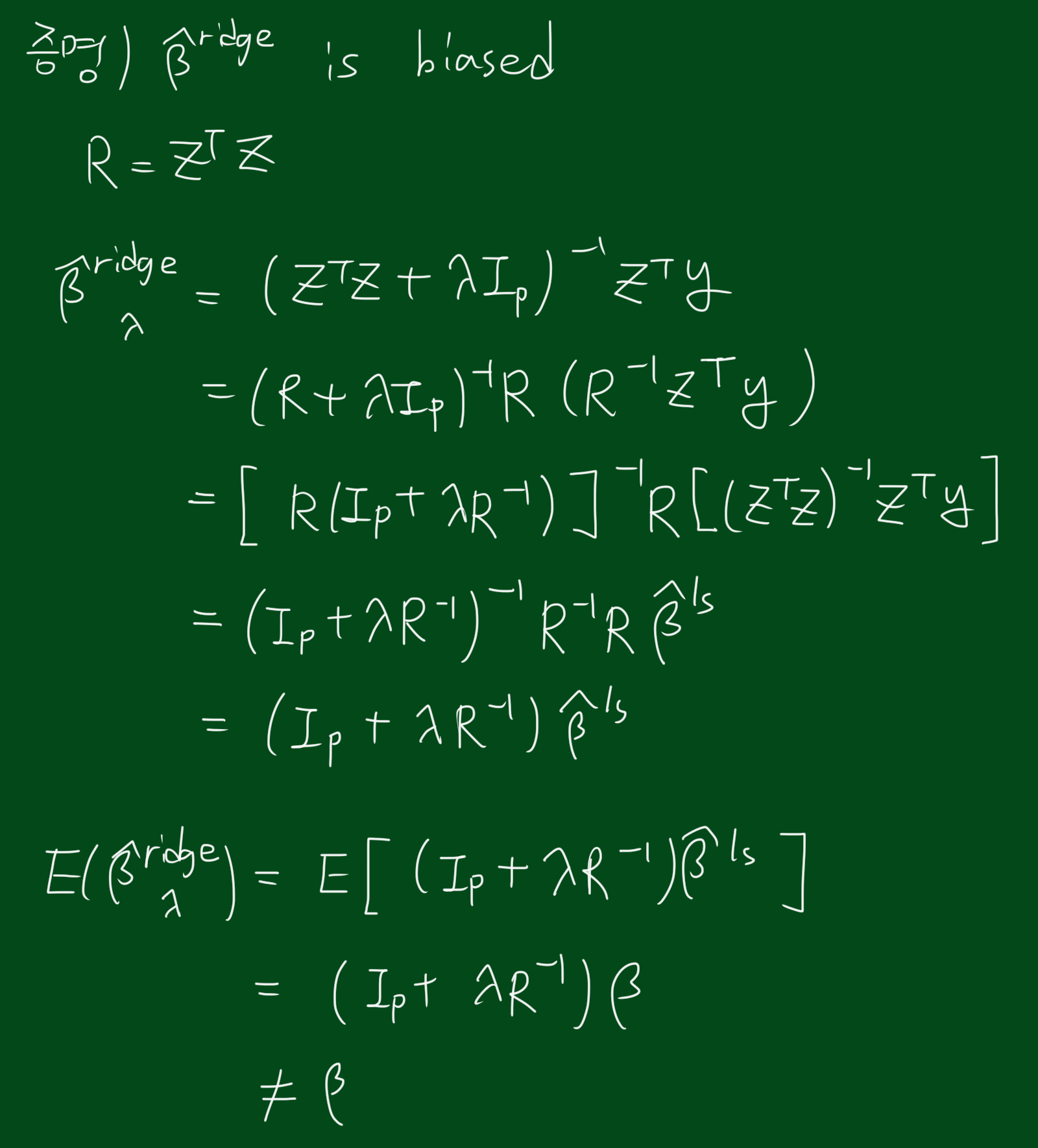
라쏘(lasso) 회귀분석
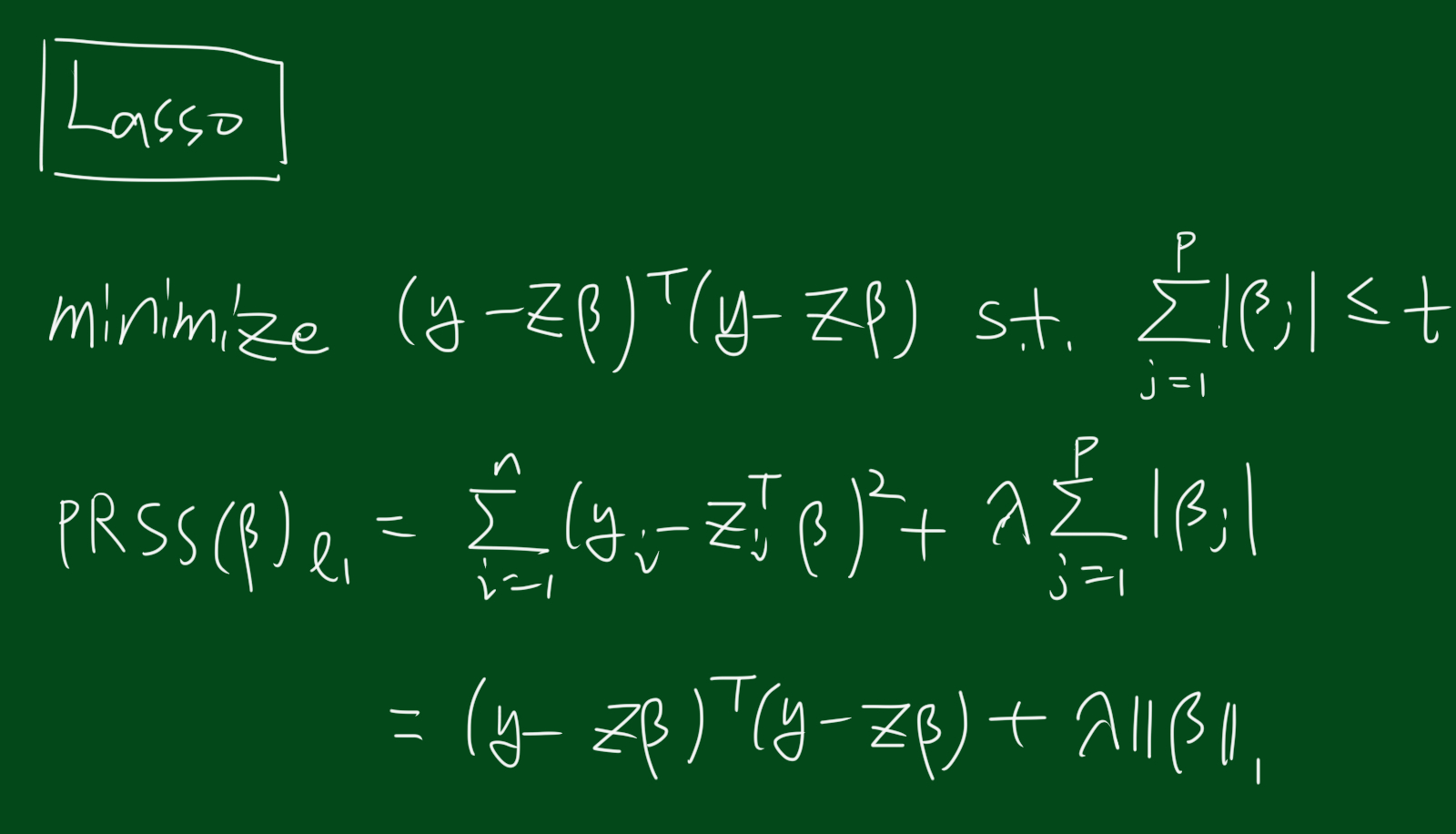
릿지와는 달리 라쏘추정량은 closed form이 없습니다. 라소추정량을 구하려면 컨벡스 최적화에서 quadratic programming 기술이 필요합니다.
라쏘 추정 과정
-
먼저 작은 $\epsilon$을 선택합니다.
-
시작은 잔차(residual) $r$을 $r=y$라고 설정하고 추정하고자하는 베타값들은 $\beta_1 =\beta_2 =\cdots=\beta_{p} = 0$이라고 설정합니다.
-
잔차 $r$과 가장 상관관계가 있는 피쳐 $Z_j(j=1,…,p)$를 선택합니다.
-
이제 베타를 업데이트해야합니다. 새로운 $\beta_j$를 기존의 $\beta_j$에서 $\delta_j$를 더한값, 즉, $\beta_j+\delta_j$로 업데이트합니다. 이때 $\delta_j$란, $\delta_j = \epsilon \cdot sign(r, Z_j) = \epsilon \cdot sign(Z_{j}^{T}r)$ 입니다.
-
새로운 잔차 $r$을 업데이트합니다. 새로운 $r$를 $r-\delta_j Z_j$로 업데이트합니다.
-
3단계~5단계를 반복합니다.


