[딥러닝] 파이토치 자세한 튜토리얼
업데이트:
파이토치 튜토리얼
참고링크
1. 서론
이번 포스팅에서는 파이토치를 처음 사용하시는 분들을 위한 튜토리얼을 작성해보겠습니다. 참고로 이번 포스트팅은 파이토치 공식 튜토리얼의 내용을 참고했으며, 해당 내용을 좀더 자세히 풀어썼다고 생각하시면 되겠습니다.
이번 튜토리얼은 3차 다항식을 이용해 사인(sin) 함수를 추정하는 문제를 다뤄보겠습니다.
2. 넘파이
먼저 넘파이 라이브러리를 활용해 문제를 풀어보겠습니다.
2.1. 라이브러리 불러오기 및 실제값 생성
import numpy as np
import math
import matplotlib.pyplot as plt
# 추정하고자 하는 실제 곡선
x = np.linspace(-math.pi, math.pi, 2000)
y = np.sin(x)
위와 같은 코드를 작성해줍니다. 위 코드는 라이브러리를 불러오고 우리가 추정하고자 하는 실제 곡선인 sin 함수값을 생성하는 코드입니다. 위 코드로부터 생성된 y값이 실제값이라고 생각하면 되겠습니다.
plt.plot(x, y)
plt.show()
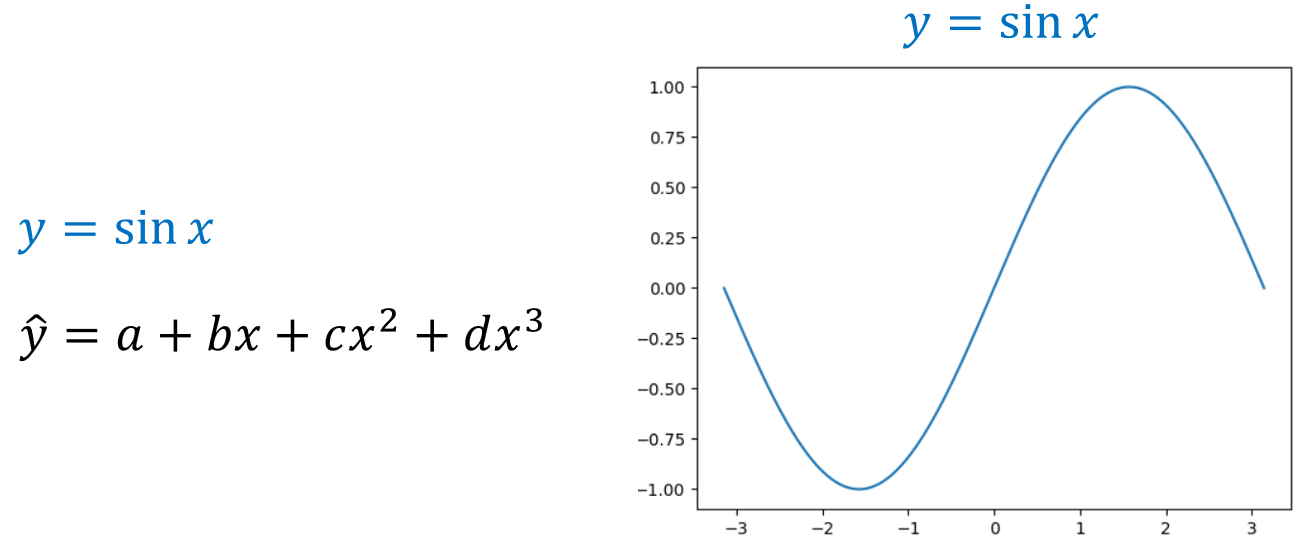
앞서 구한 y값을 시각화하면 위 그림과 같이 사인곡선이 나타나는 것을 볼 수 있습니다. 즉, 우리는 3차 다항식을 이용해 위 곡선을 추정하는 것이 목표입니다.
즉, 위 3차 다항식의 a, b, c, d를 딥러닝을 이용해 추정하는 것입니다.
2.2. 가중치 초기값 생성
# 가중치 초기
a = np.random.randn()
b = np.random.randn()
c = np.random.randn()
d = np.random.randn()
다음으로 가중치의 초기값을 정해줍니다. 초기값은 위 코드처럼 랜덤으로 정해줍니다.
>>> print(a, b, c, d)
0.1629 -0.563484 2.5714189 -0.062937
앞서만든 초기값을 확인해봅니다.
2.3. 학습
# 학습
learning_rate = 1e-6
for t in range(0, 1000):
y_pred = a + b*x + c*x**2 + d*x**3
ss = np.square(y_pred - y)**0.5
loss = ss.sum()
if t%100 == 99:
print(t, loss)
grad_y_pred = 2.0 * (y_pred - y)
grad_a = grad_y_pred.sum()
grad_b = (grad_y_pred*x).sum()
grad_c = (grad_y_pred*x**2).sum()
grad_d = (grad_y_pred*x**3).sum()
a -= learning_rate * grad_a
b -= learning_rate * grad_b
c -= learning_rate * grad_c
d -= learning_rate * grad_d
위 코드는 학습하는 코드인데, 코드가 길기 때문에 나눠서 보겠습니다.
# 학습
learning_rate = 1e-6
for t in range(0, 1000):
y_pred = a + b*x + c*x**2 + d*x**3
위 코드에서 learning_rate는 이름 그대로 학습율을 의미합니다. 그리고 반복문을 수행하는데 학습은 1000번 수행하며, 우리가 만든 추정식을 통해 구한 y의 추정값(예측값)을 y_pred라고 이름지어 줍니다.
ss = np.square(y_pred - y)**0.5
loss = ss.sum()
if t%100 == 99:
print(t, loss)
그리고 다음 단계로 비용함수를 정의해주는데, 이번 실습에서 비용함수는 오차제곱합으로 하겠습니다. 따라서 오차제곱합 ss를 통해 구한 손실의 총합이 위 식에서 loss가 되는 것입니다.
grad_y_pred = 2.0 * (y_pred - y)
grad_a = grad_y_pred.sum()
grad_b = (grad_y_pred*x).sum()
grad_c = (grad_y_pred*x**2).sum()
grad_d = (grad_y_pred*x**3).sum()
그리고 다음으로 그래디언트를 계산해줍니다. 위와 같은 방법으로 코딩하는 이유는 다음과 같습니다.
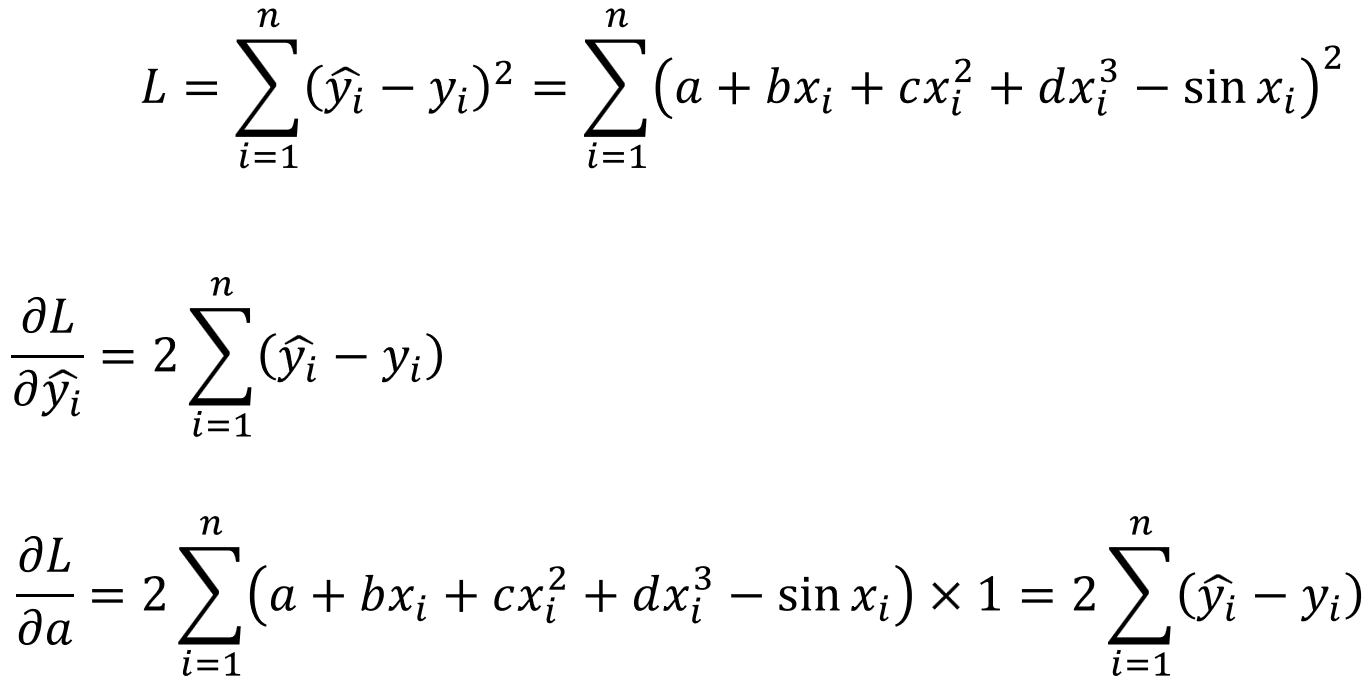
위 식에서 오차제곱합을 이용해 비용함수를 L로 정의하고 a에 대해 편미분한 값을 이용해 그래디언트를 구할 수 있습니다.
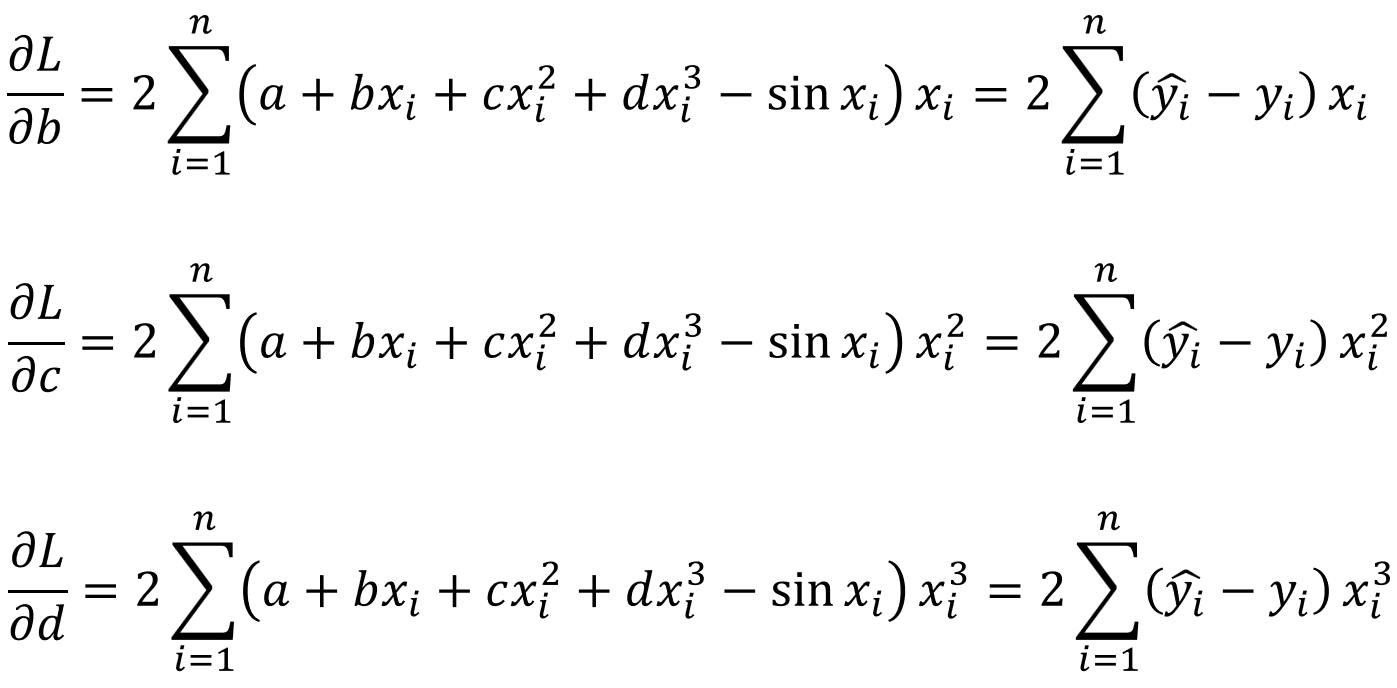
그리고 나머지 친구들에 대해서도 위와 같이 구할 수 있습니다.
a -= learning_rate * grad_a
b -= learning_rate * grad_b
c -= learning_rate * grad_c
d -= learning_rate * grad_d
마지막 단계로 가중치를 업데이트 시킵니다. 위 코드는 다음 식을 이용해 작성한 것입니다.
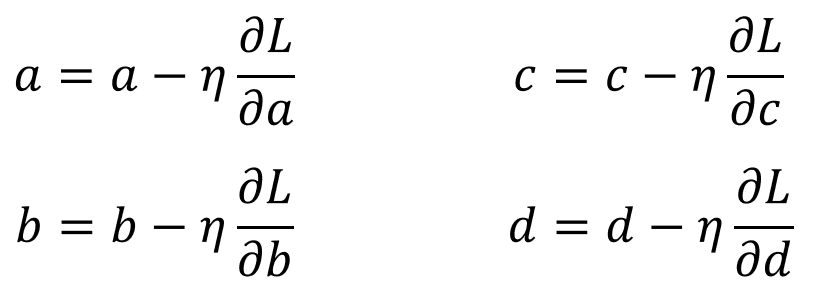
2.4. 학습 결과
학습이 끝나고 최종 학습 결과인 a, b, c, d를 출력하면 다음과 같습니다.
# 학습 결과
>>> print(f"Result: y = {a} + {b} x + {c} x^2 + {d} x^3")
Result: y = -0.04471609 + 0.87041 x + 0.0077142708 x^2 + -0.095275 x^3
그리고 실제로 학습이 얼마나 잘 되었는지, 실제 곡선과 추정 곡선을 비교하면 다음과 같습니다.
plt.plot(x, y, color='blue')
plt.plot(x, y_pred, color='red')
plt.show()
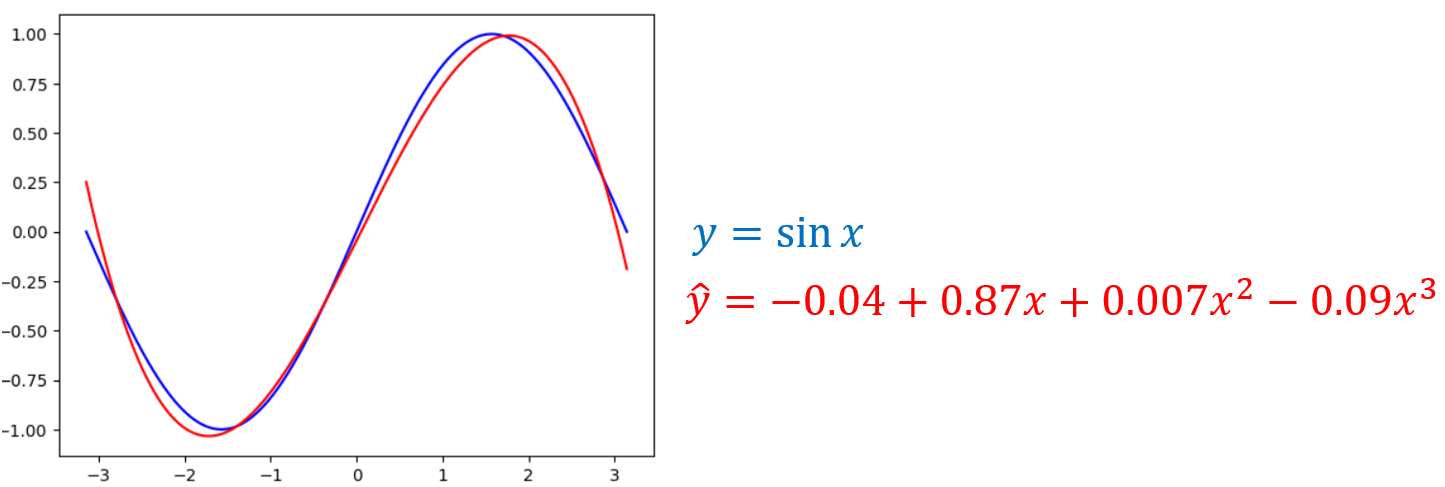
2.5. 전체 코드
# 전체 코드
import numpy as np
import math
import matplotlib.pyplot as plt
# 추정하고자 하는 실제 곡선
x = np.linspace(-math.pi, math.pi, 2000)
y = np.sin(x)
# 가중치 초기
a = np.random.randn()
b = np.random.randn()
c = np.random.randn()
d = np.random.randn()
# 학습
learning_rate = 1e-6
for t in range(0, 1000):
y_pred = a + b*x + c*x**2 + d*x**3
ss = np.square(y_pred - y)**0.5
loss = ss.sum()
if t%100 == 99:
print(t, loss)
grad_y_pred = 2.0 * (y_pred - y)
grad_a = grad_y_pred.sum()
grad_b = (grad_y_pred*x).sum()
grad_c = (grad_y_pred*x**2).sum()
grad_d = (grad_y_pred*x**3).sum()
a -= learning_rate * grad_a
b -= learning_rate * grad_b
c -= learning_rate * grad_c
d -= learning_rate * grad_d
# 학습 결과
print(f"Result: y = {a} + {b} x + {c} x^2 + {d} x^3")
3. 파이토치
위 코드를 파이토치를 이용해 작성하면 다음과 같습니다.
import torch
import math
dtype = torch.float
device = torch.device('cpu')
x = torch.linspace(-math.pi, math.pi, 2000, device=device, dtype=dtype)
y = torch.sin(x)
a = torch.randn((), device=device, dtype=dtype)
b = torch.randn((), device=device, dtype=dtype)
c = torch.randn((), device=device, dtype=dtype)
d = torch.randn((), device=device, dtype=dtype)
learning_rate = 1e-6
for t in range(2000):
y_pred = a + b * x + c * x ** 2 + d * x ** 3
ss = (y_pred - y).pow(2)
loss = ss.sum().item()
if t % 100 == 99:
print(t, loss)
grad_y_pred = 2.0 * (y_pred - y)
grad_a = grad_y_pred.sum()
grad_b = (grad_y_pred * x).sum()
grad_c = (grad_y_pred * x ** 2).sum()
grad_d = (grad_y_pred * x ** 3).sum()
a -= learning_rate * grad_a
b -= learning_rate * grad_b
c -= learning_rate * grad_c
d -= learning_rate * grad_d
print(f'Result: y = {a.item()} + {b.item()} x + {c.item()} x^2 + {d.item()} x^3')
4. iris 데이터 분류 학습하기
import pandas as pd
from sklearn.model_selection import train_test_split
import torch
import torch.nn as nn
import torch.optim as optim
# parameters
learning_rate = 0.01
epochs = 1000
df = pd.read_csv("./iris.csv")
X = df[["sepal_length","sepal_width","petal_length","petal_width"]].values
y = df["class"].values
X = torch.tensor(X, dtype=torch.float32)
y = torch.tensor(y, dtype=torch.long)
X_tn, X_te, y_tn, y_te = train_test_split(X, y, random_state=777)
class IrisNet(nn.Module):
def __init__(self):
super(IrisNet, self).__init__()
self.layer1 = nn.Linear(4, 10)
self.layer2 = nn.Linear(10, 3)
def forward(self, x):
x = torch.relu(self.layer1(x))
x = self.layer2(x)
return x
mymodel = IrisNet()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(mymodel.parameters(), lr=learning_rate)
for epoch in range(epochs):
optimizer.zero_grad()
outputs = mymodel(X_tn)
cost = criterion(outputs, y_tn)
cost.backward()
optimizer.step()
if (epoch+1) % 100 == 0:
print('Epoch [%d/%d], Loss: %.4f' % (epoch+1, epochs, cost.item()))
Epoch [100/1000], Loss: 0.9430
Epoch [200/1000], Loss: 0.7136
Epoch [300/1000], Loss: 0.5374
Epoch [400/1000], Loss: 0.4417
Epoch [500/1000], Loss: 0.3793
Epoch [600/1000], Loss: 0.3315
Epoch [700/1000], Loss: 0.2925
Epoch [800/1000], Loss: 0.2606
Epoch [900/1000], Loss: 0.2345
Epoch [1000/1000], Loss: 0.2132
with torch.no_grad():
prediction = mymodel(X_te)
correct_prediction = torch.argmax(prediction, 1) == y_te
accuracy = correct_prediction.float().mean()
print('Accuracy:', accuracy.item())
1.0


