[기초통계] 이항분포, 베르누이분포
업데이트:
이항분포와 베르누이 분포
참고링크
1. 이항분포
이항분포(binomial distribution)은 연속된 n번의 독립시행에서 각 시행이 확률 p를 가질 떄의 이산확률분포이다.
이항분포를 설명하기 위해 주사위를 다섯번 던져 1이 나온 횟수를 구하고자 하는 예를 들어보겠습니다. 주사위를 다섯번 던지므로 n=5 입니다. 또한 주사위이기 때문에 1이나올 확률 p=1/6에 해당합니다. 그리고 확률변수는 1이 나온 횟수입니다.
이항분포의 정의를 살펴보면 독립시행이라는 말이 나옵니다. 독립시행이란 이전 시행이 다음 시행의 확률에 영향을 주지 않는다는 뜻입니다. 예를 들어, 주사위를 던졌을 때 1이 나올 확률이 1/6이라고하면 첫번째 던졌을때 1이 나왔다고 해도, 두번째 던졌을 때 1이 나올 확률에 영향을 주지 않는다는 것이죠. 즉, 첫번째 던졌을때나…백번째 던졌을때나 주사위 1이 나올 확률은 동일하게 1/6이라는 뜻입니다.
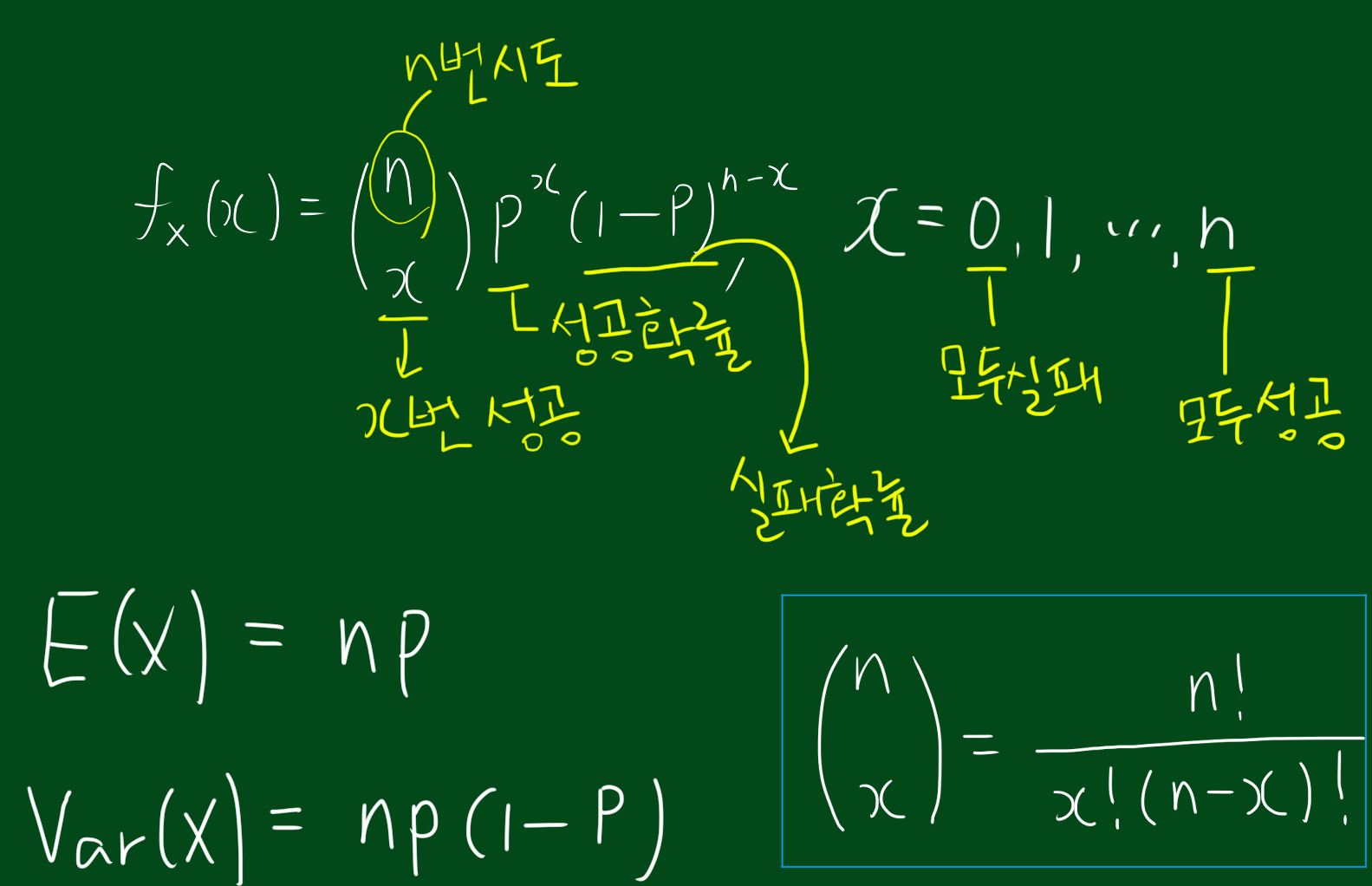
2. 베르누이 분포
이항분포에서 n=1일 때, 베르누이분포 라고 한다.
베르누이분포는 이항분포의 특수한 경우 입니다.
이항분포에서 n이 1인 경우, 즉, 주사위를 한번만 던졌을때라고 생각하시면 됩니다.
베르누이분포는 주사위를 한 번만 던지므로 베르누이시행이라고도 합니다.
따라서 베르누이시행을 여러번 한 것이 이항분포라고 할 수 있는 것이죠.
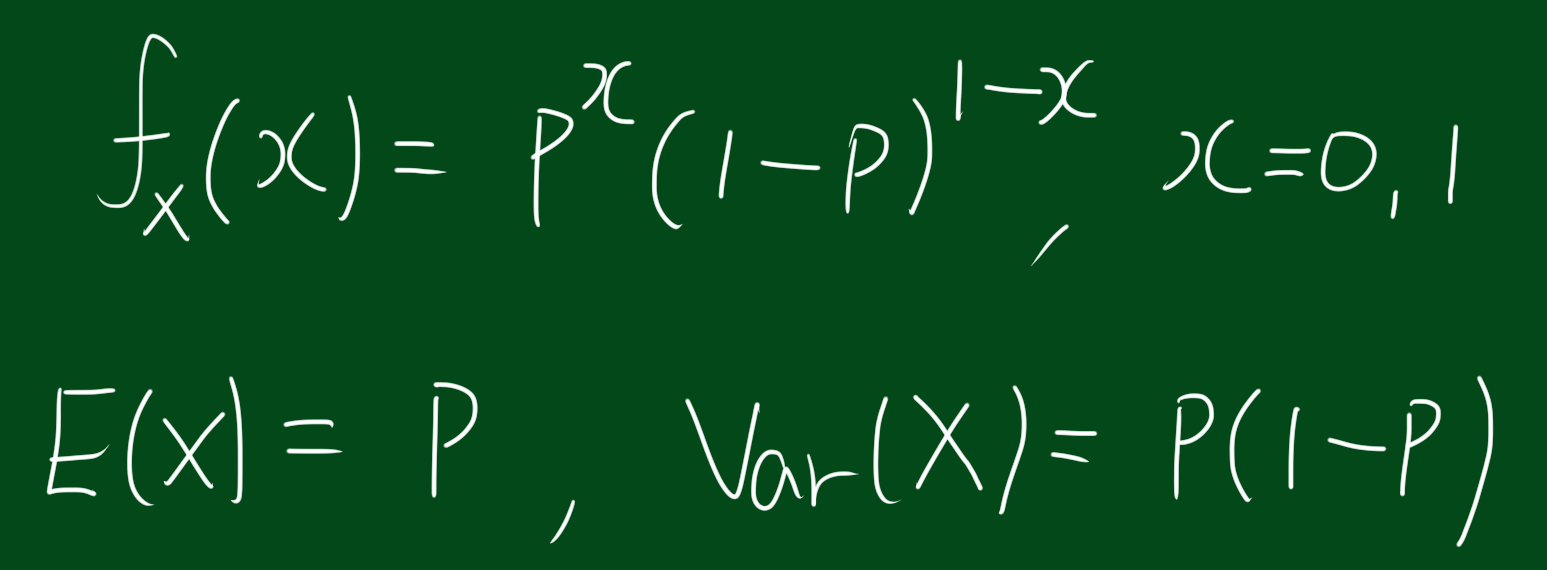
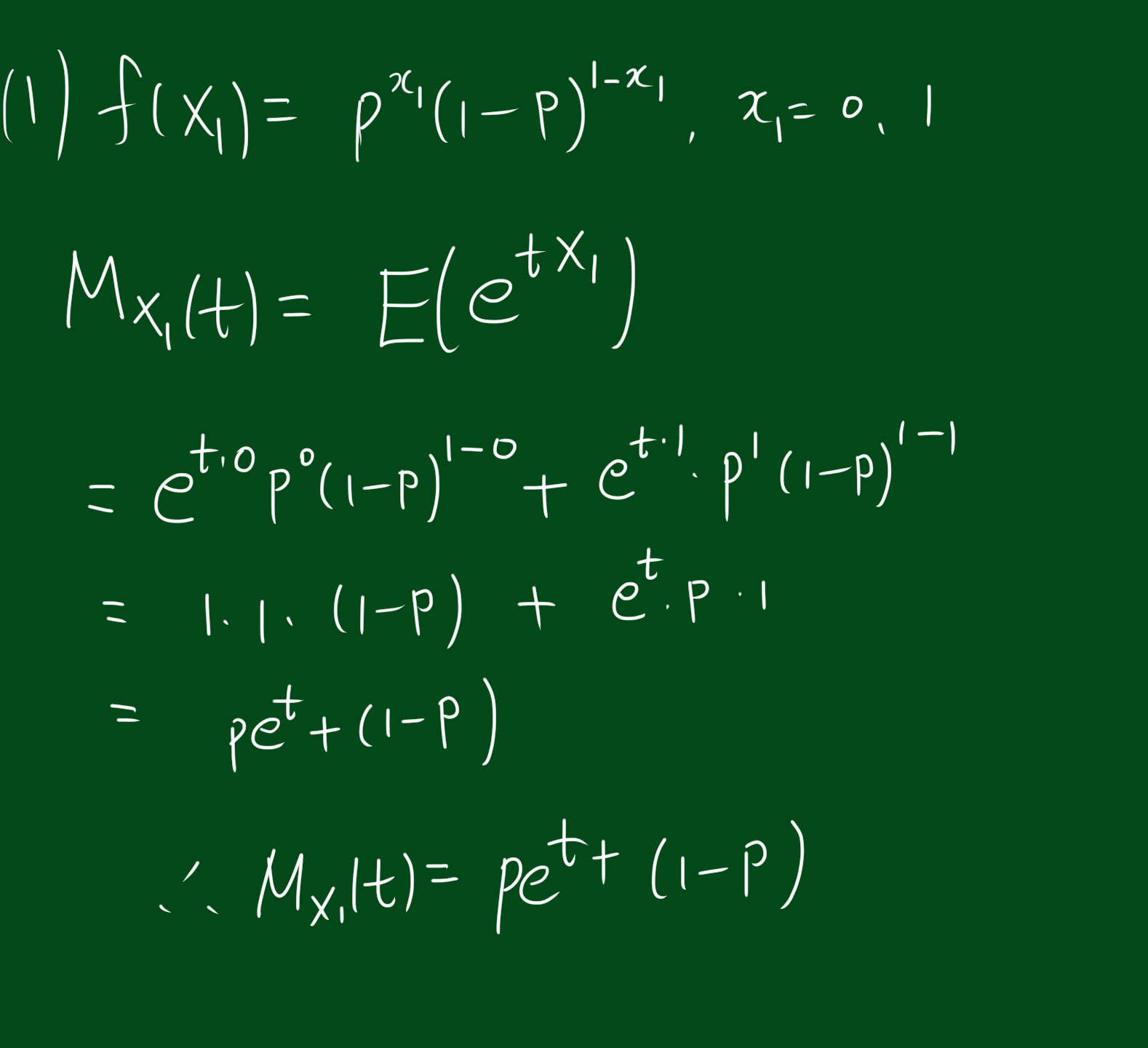
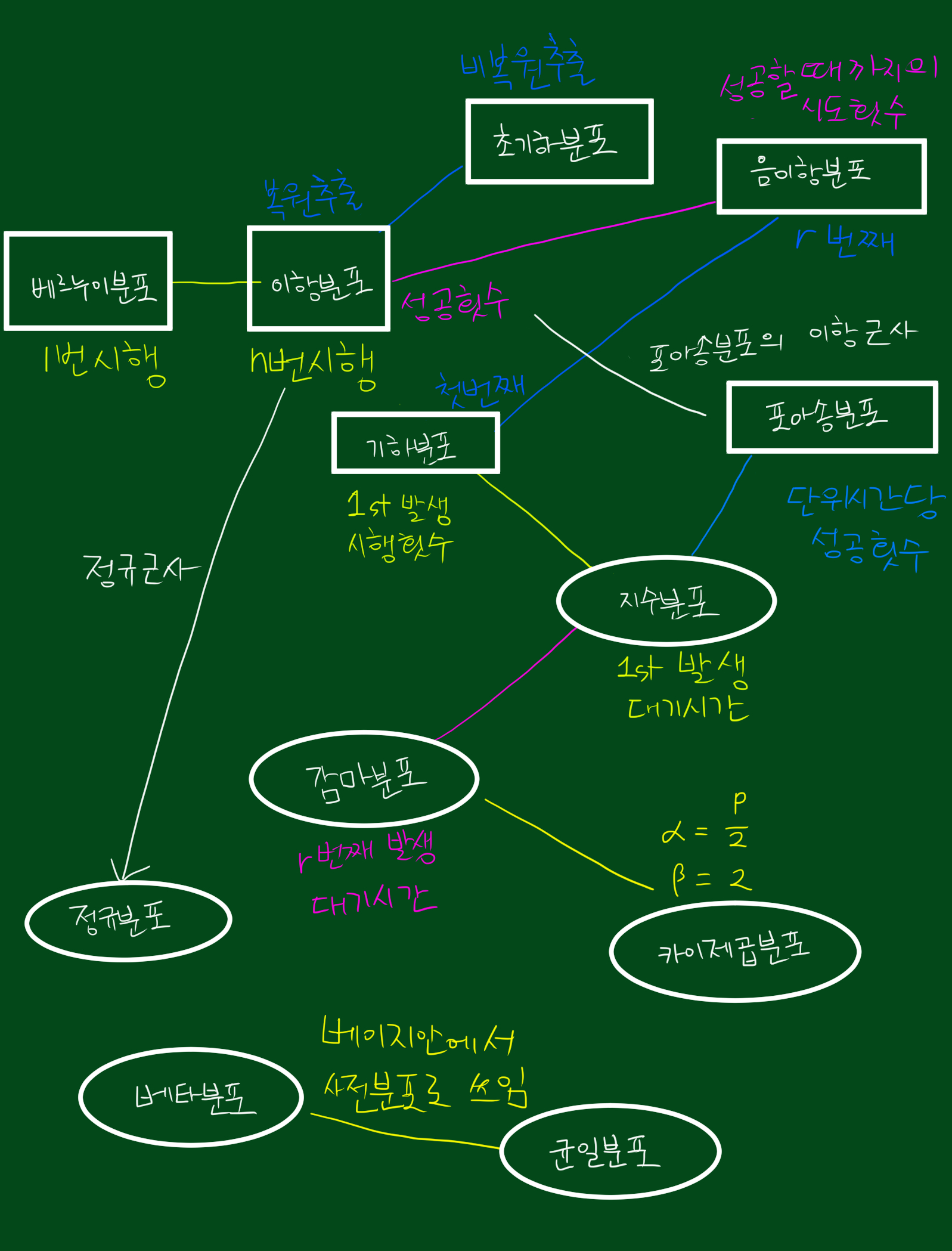
참고. 확률분포간 관계도