[기초통계] 카이제곱분포 의미 및 개념 정리

카이제곱분포 의미 및 개념 정리

참고링크

• 확률변수 복습하기
• 확률분포 복습하기
• 모집단과 표본 복습하기
• 평균과 분산 복습하기
• 공분산, 상관계수 복습하기
• 최대가능도추정 복습하기

  이산확률분포

• 베르누이분포, 이항분포
• 기하분포, 음이항분포
• 초기하분포
• 포아송분포

  연속확률분포

• 정규분포
• 감마분포
• 지수분포
• 카이제곱분포
• 베타분포
• 균일분포

1. 카이제곱분포의 정의

카이제곱분포(chi-squared distribution)은 p개의 서로 독립적인 표준정규 확률변수를 각각 제곱한 다음 합해서 얻어지는 분포이다. 이 때 p를 자유도라고 하며, 카이제곱분포의 매개변수가 된다. 카이제곱 분포는 신뢰구간이나 가설검정 등의 모델에서 자주 등장한다.

2. 카이제곱분포의 확률밀도함수, 평균, 분산

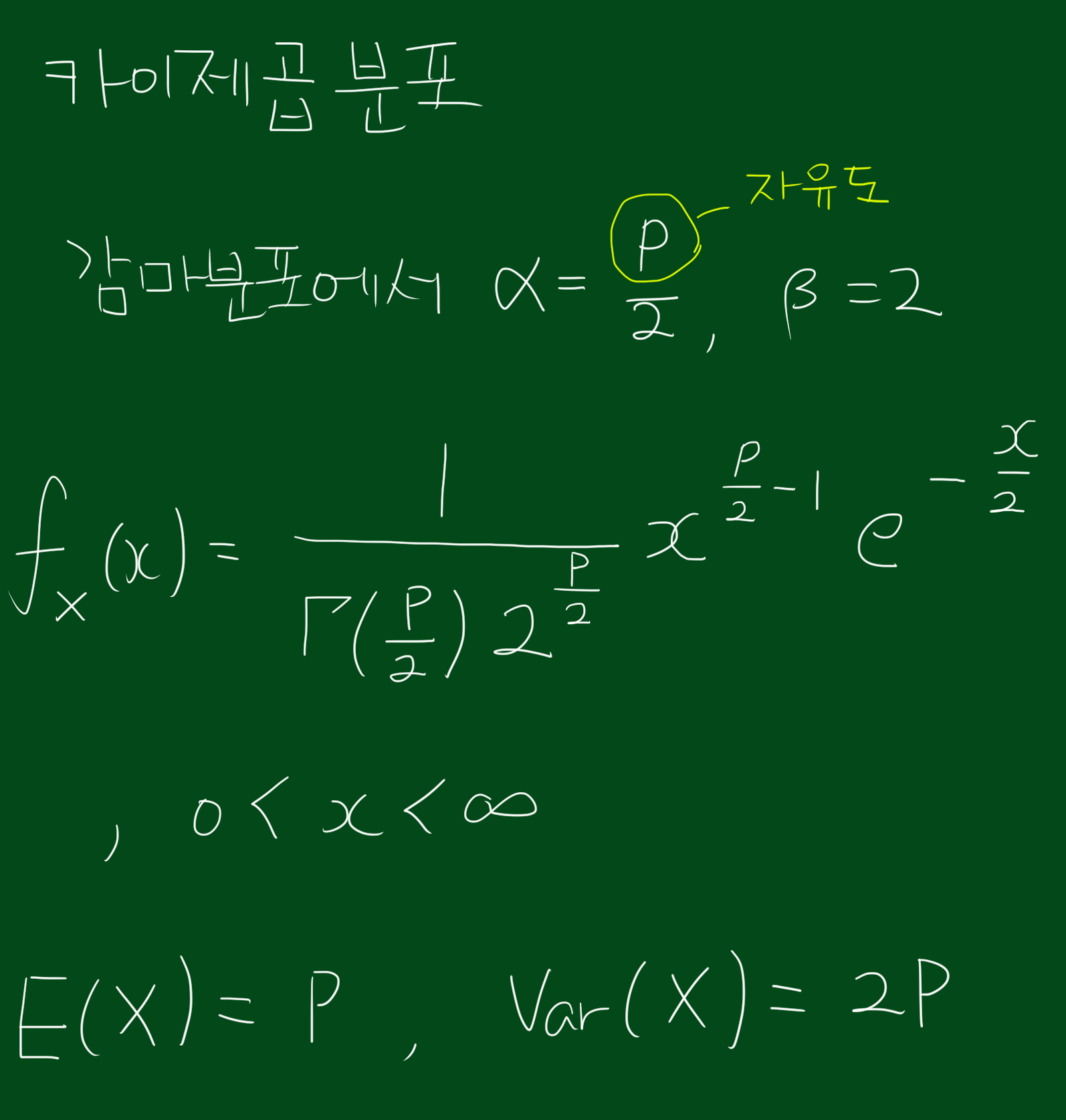
2. 감마분포와의 관계

사실 카이제곱분포는 감마분포의 특수한 경우라고 생각하실수 있습니다. 카이제곱분포는 감마분포에서 $\alpha = p/2$, $\beta = 2$인 경우를 나타냅니다. 따라서 감마분포를 이해하고 계신다면 카이제곱분포도 쉽게 이해하실수 있습니다.

3. 표준정규분포와의 관계

카이제곱분포의 정의에서 알 수 있듯, 카이제곱분포는 표준정규확률변수를 각각 제곱한 다음 합새서 얻어지는 분포인데요. 쉽게 말해 표준정규확률변수를 제곱해서 더하면 카이제곱분포가 되는 것인데요. 이를 수식으로 정리하면 아래와 같습니다.

표준정규 확률변수 $X_{1}, \dots , X_{p}$가 있다고 가정하면

\[Q = \sum_{i=1}^{p} X_{i}^{2}\]

는 자유도 p의 카이제곱분포입니다. 이를 $ Q \sim \chi_{p}^{2}$ 으로 표현합니다.

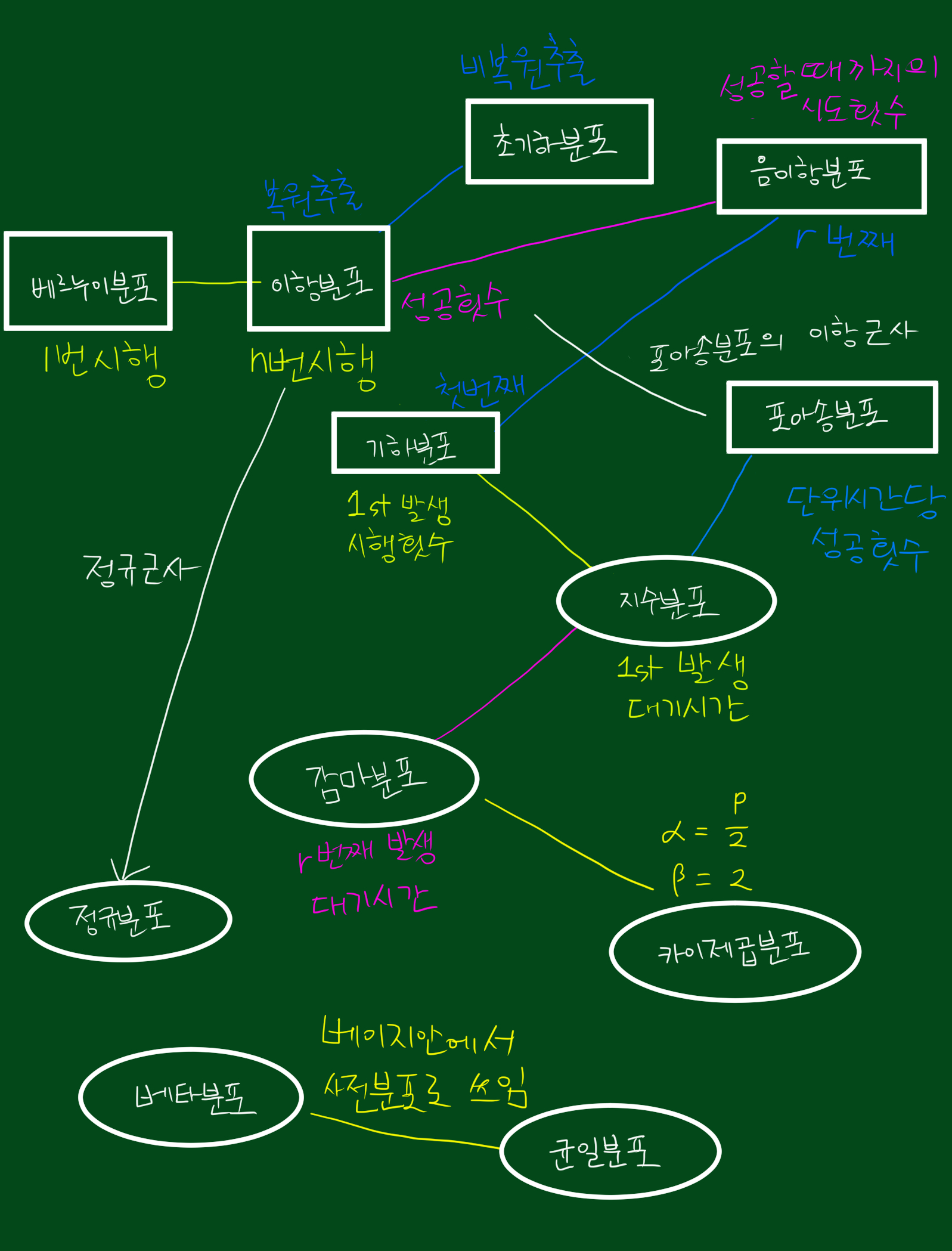
참고. 확률분포간 관계도