[기초통계] 기하분포 및 음이항분포 정리

기하분포 및 음이항분포 정리

참고링크

머신러닝	딥러닝	선형대수	기초통계	최적화
k-means	신경망이란	고유값,고유벡터	확률변수	컨벡스 셋
k-최근접이웃	성능함수	행렬식	확률분포	컨벡스 함수
선형회귀	신경망 학습	내적	모집단과 표본	라그랑주 듀얼
로지스틱회귀	교차연결	기저	평균과 분산	KKT 조건
릿지,라쏘회귀	합성곱 신경망	랭크, 차원	공분산, 상관계수	ROC 커브
의사결정나무	배치, 에포크 차이	선형변환	최대가능도추정	크로스 밸리데이션
서포트벡터머신	텐서플로기초(1)	직교행렬	베르누이,이항분포	실루엣 스코어
원클래스 SVM	텐서플로기초(2)	고유값분해	기하,음이항분포
LDA	seq2seq	특이값분해	초기하분포
GMM	opencv기초		포아송분포
부스팅	resnet		정규분포
사이킷런 실습	다각형내부판별		감마분포
	엣지판별		지수분포
			카이제곱분포
			베타분포
			균일분포

1. 기하분포

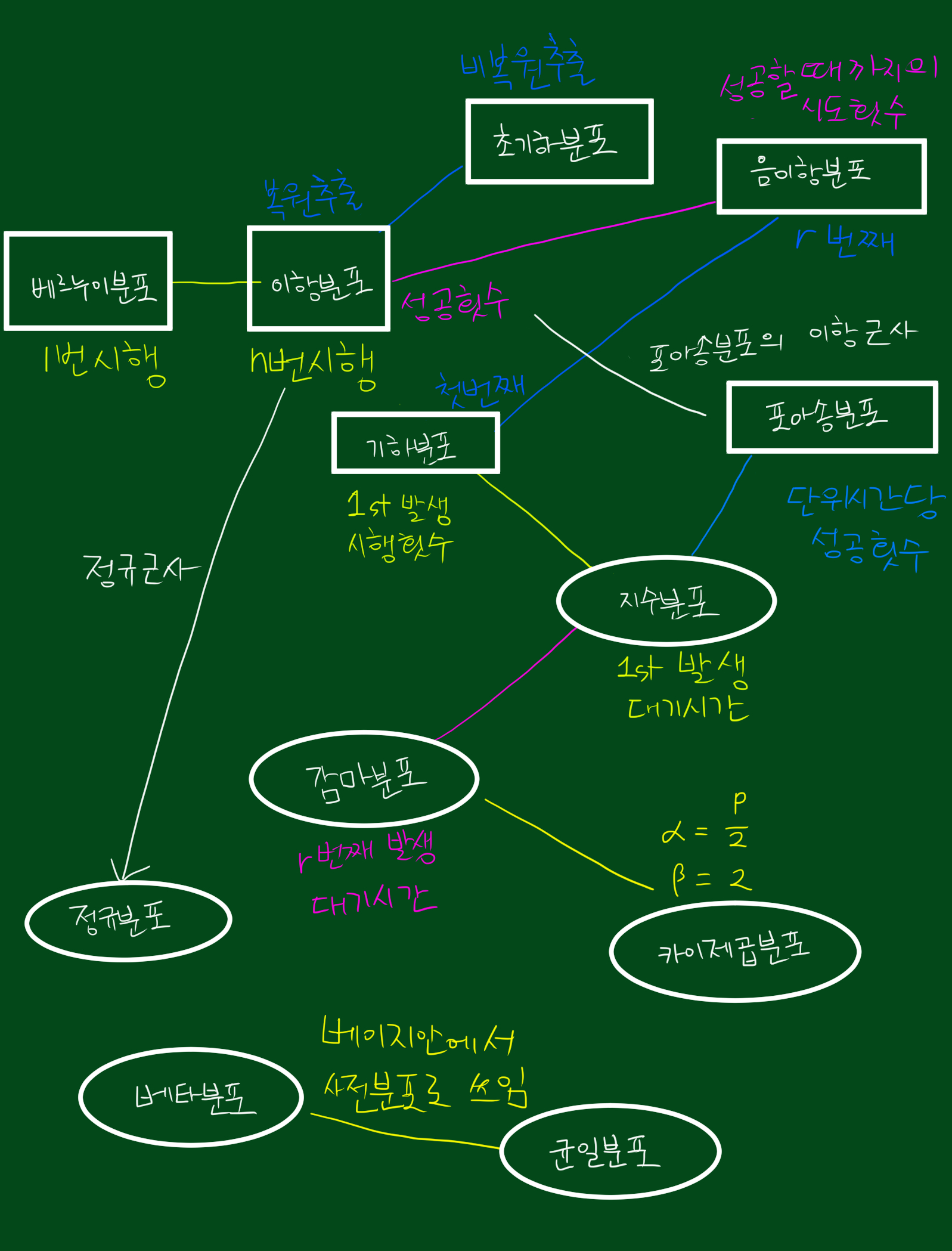
기하분포(geometric distribution)는 이산확률분포 중 하나로 특이하게 두 가지 관점으로 볼 수 있습니다.

• 베르누이시행에서 처음 성공까지 시도한 횟수 X의 분포
• 베르누이시행에서 처음 성공까지 실패한 횟수 Y=X-1의 분포

즉, 기하분포는 어떤 행위를 성공할때까지 시도하는데, 성공할때까지의 시도횟수 또는 실패한 횟수의 분포라고 볼 수 있습니다. 이산확률분포는 많은 경우 베르누이시행을 기반으로 이루어져있습니다.
아래에 기하분포를 간략히 정리해보았습니다.

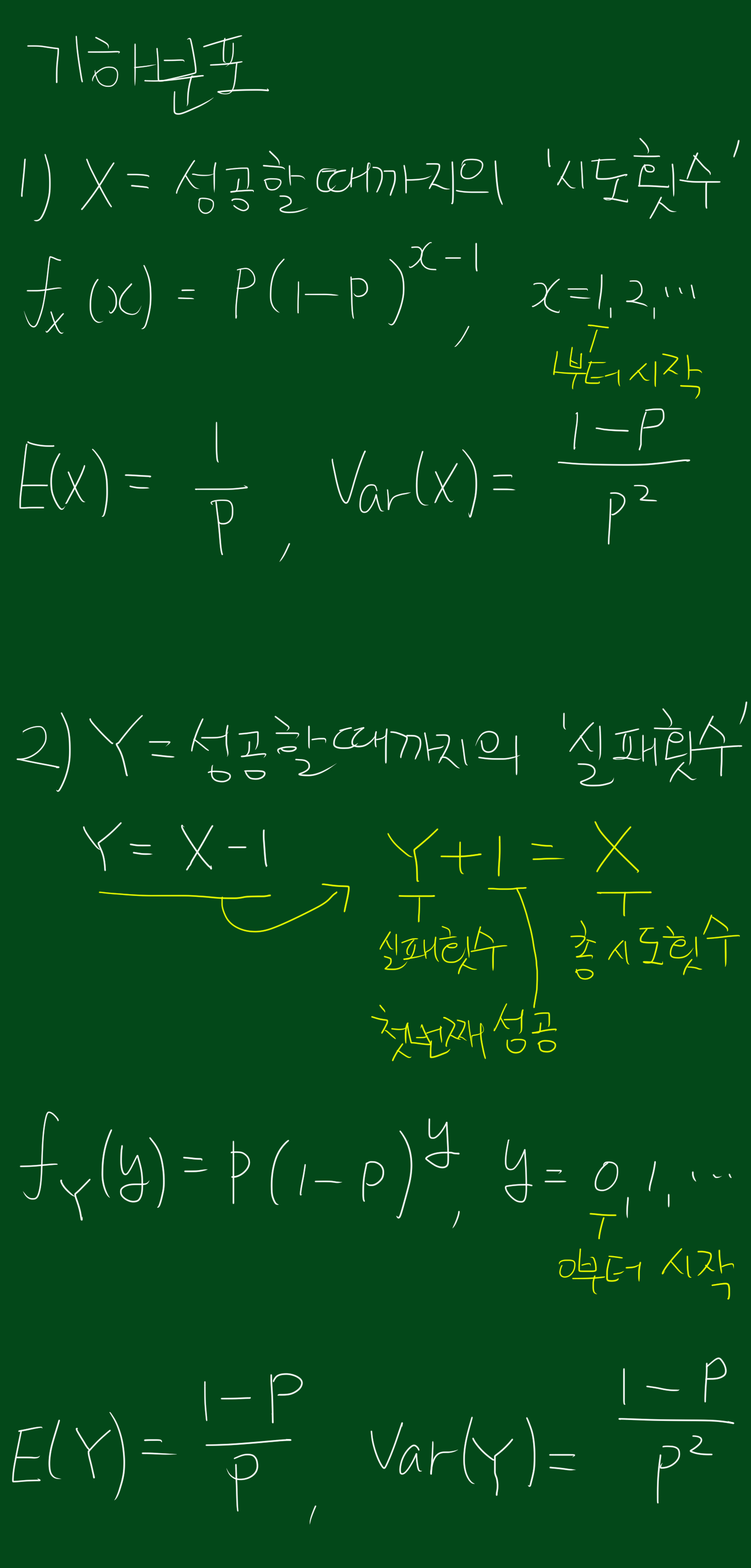
기하분포는 두가지 관점으로 정의될 수 있으므로 기하분포를 사용할때는 기준을 시도한 횟수로 볼 것인지, 실패한 횟수로 볼것인지를 명확히 해야합니다.

기하분포는 처음 성공까지를 보는데요. 그럼 r번째 성공 까지 보면 어떻게 될까요? 기하분포를 일반화한 버전이 음이항분포 입니다.

2. 음이항분포

음이항분포는 기하분포를 일반화시킨 것이므로, 아래와 같이 정의 할 수 잇습니다.

• 베르누이시행에서 r번째 성공까지 시도한 횟수 X의 분포
• 베르누이시행에서 r번쨰 성공까지 실패한 횟수 Y=X-r의 분포

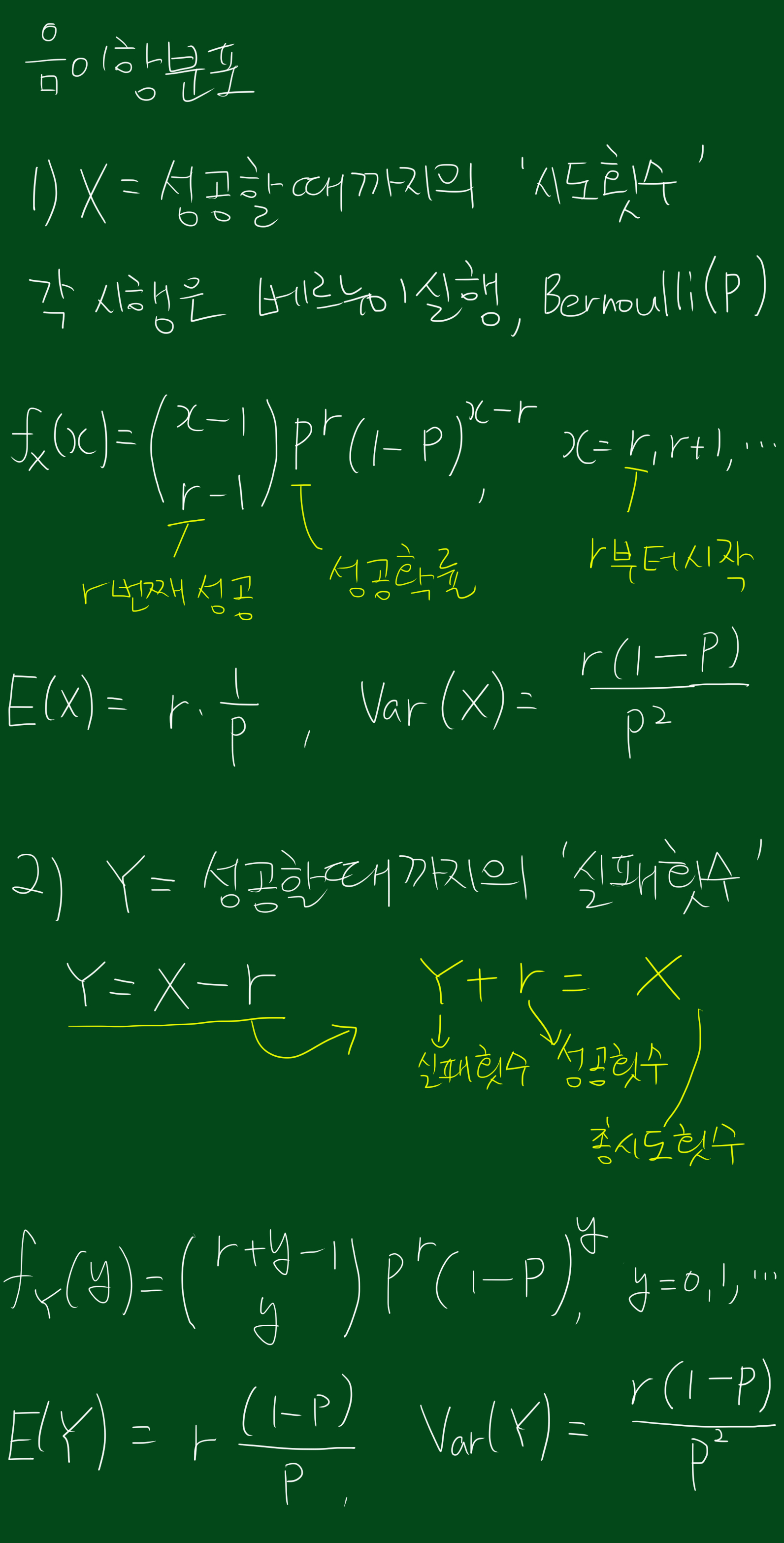
추가적으로 r=3일 경우의, 음이항 분포의 mgf를 구해보았습니다.

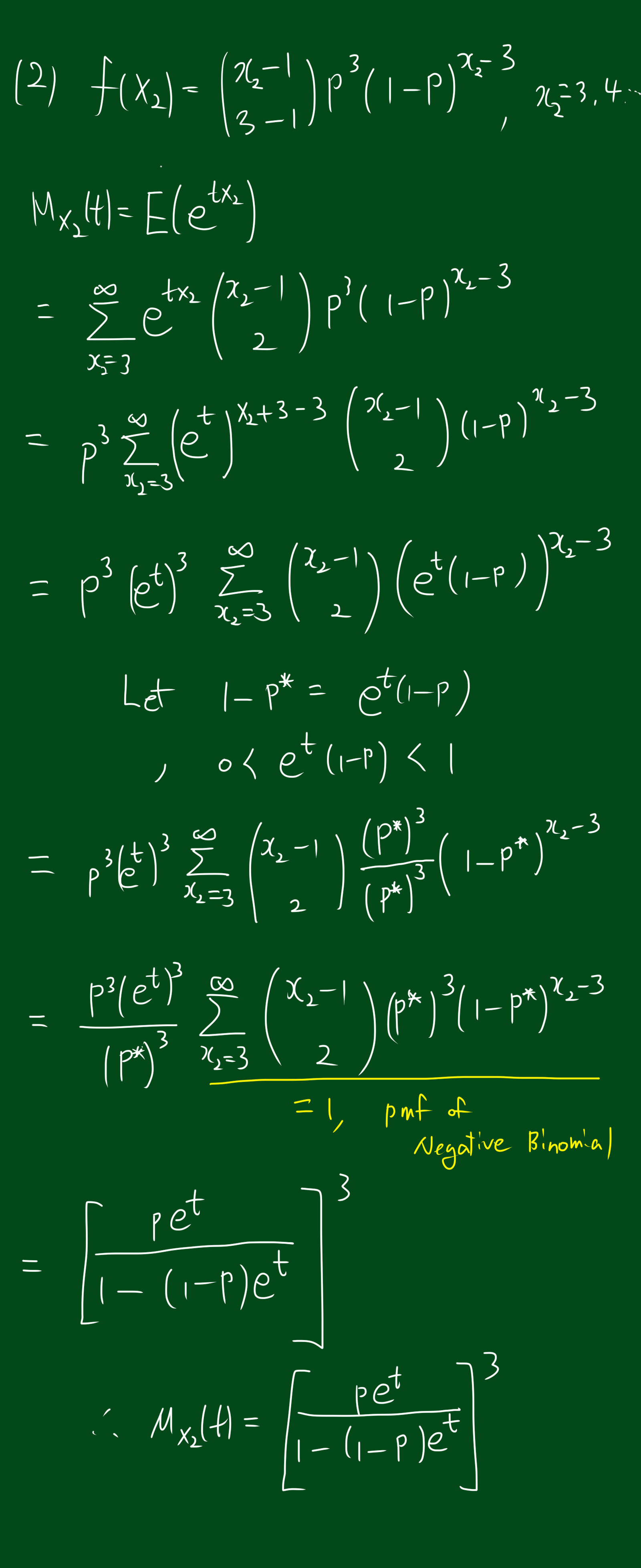
참고. 확률분포간 관계도