[기초통계] 평균과 분산의 의미, 개념

평균(mean)과 분산(variance)

참고링크

머신러닝	딥러닝	선형대수	기초통계	최적화
k-means	신경망이란	고유값,고유벡터	확률변수	컨벡스 셋
k-최근접이웃	성능함수	행렬식	확률분포	컨벡스 함수
선형회귀	신경망 학습	내적	모집단과 표본	라그랑주 듀얼
로지스틱회귀	교차연결	기저	평균과 분산	KKT 조건
릿지,라쏘회귀	합성곱 신경망	랭크, 차원	공분산, 상관계수	ROC 커브
의사결정나무	배치, 에포크 차이	선형변환	최대가능도추정	크로스 밸리데이션
서포트벡터머신	텐서플로기초(1)	직교행렬	베르누이,이항분포	실루엣 스코어
원클래스 SVM	텐서플로기초(2)	고유값분해	기하,음이항분포
LDA	seq2seq	특이값분해	초기하분포
GMM	opencv기초		포아송분포
부스팅	resnet		정규분포
사이킷런 실습	다각형내부판별		감마분포
	엣지판별		지수분포
			카이제곱분포
			베타분포
			균일분포

0. 대표값

이전에는 확률변수, 표본에 대해 알아보았습니다. 표본추출로 구한 표본데이터는 분포를 따르게 되는데요. 분포의 특성을 나타내는데 대표값이라는 개념을 사용합니다. 대표값은 이름 그대로 데이터셋을 대표하는 값을 의미합니다. 그리고 가장 흔히 쓰이는 대표값은 평균, 분산, 표준편차 등이 있습니다.

1. 평균(mean)과 기대값(expected value)

1-1. 평균(mean)

평균에는 산술평균, 기하평균, 조화평균과 같이 여러 종류가 있는데요. 오늘 알아볼 평균은 산술평균 입니다.

평균은 단순히 모든 관측값을 더해서 관측값 개수로 나눈 것이다.

평균은 데이터의 중심을 나타내는데 사용됩니다. 가끔 평균 대신 기대값이라는 용어를 사용하기도 하는데요. 그렇다면 기대값은 무엇일까요?

1-2. 기대값(expected value)

기대값은 각 사건이 벌어졌을 때의 이득과 그 사건이 벌어질 확률을 곱한 것을 전체 사건에 대해 합한 값이다. 이것은 어떤 확률적 사건에 대한 평균의 의미로 생각할 수 있다.

1-3. 평균과 기대값의 차이

사실 기대값은 평균과 동일하다고 생각해도 크게 문제 되지는 않을 것 같아요. 실제로 두 용어를 섞어서 사용하기도 하는데요.
저는 평균과 기대값에는 관점의 차이가 있다고 생각합니다. 즉, 표본으로부터 얻어진 표본데이터값의 연산 자체에 중점을 두고 보면 평균이고, 확률변수에 중점을 두고 보면 기대값이라고 생각합니다. 다른 말로하면 표본은 데엍로부터 이미 구해진 데이터의 평균, 기대값은 아직 구해지지않은 값(미래에 기대되는)에 대한 평균이라고도 볼 수 있을 것 같아요.

1-4. 중앙값(median)

중앙값(median) 또는 중위수는 어떤 주어진 값들을 크기의 순서대로 정렬했을 때 가장 중앙에 위치하는 값을 의미한다. 예를 들어 1, 2, 100의 세 값이 있을 때, 2가 가장 중앙에 있기 때문에 2가 중앙값이다.

중앙값은 이름그대로 값을 크기순으로 나열했을 때 가장 중앙에 위치하는 값을 의미합니다.

1-5. 평균과 중앙값의 차이

평균에 비해 중앙값은 사용빈도가 떨어지는 경향이 있는데요. 평균이 모든 상황에서 좋은 것은 아니며, 상황에 따라 평균보다 중앙값이 나은 경우도 존재합니다. 평균을 쓸지 중앙값을 쓸지는 데이터의 분포에 따라 결정되는데요.

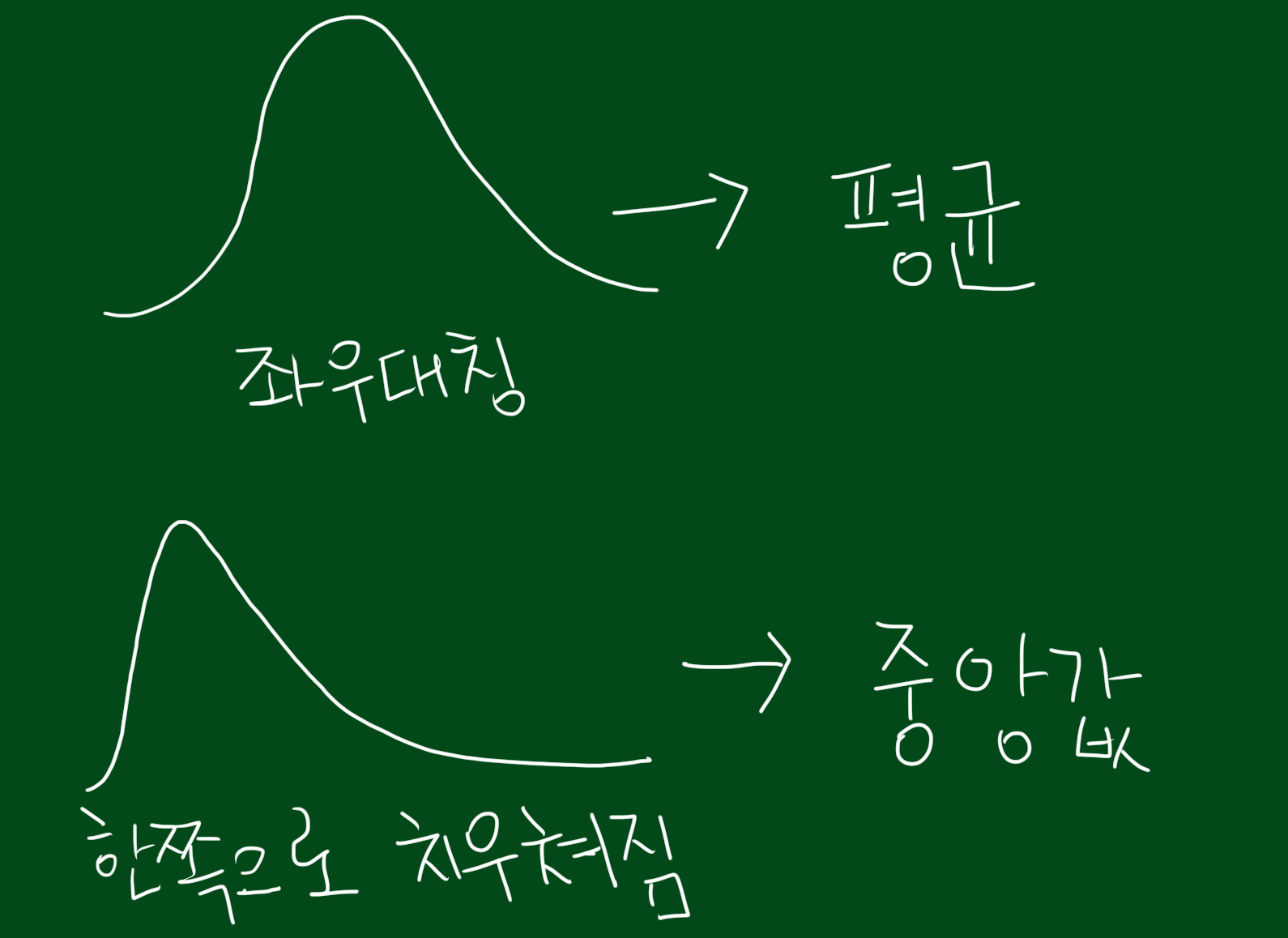
위 그림 처럼 데이터가 대칭 형태로 분포한다면, 대표값으로 평균이 적절합니다. 하지만 한쪽으로 치우처진 데이터의 경우에는 평균보다 중앙값이 더 적절합니다. 현실세계에선 대칭형태보다 한쪽으로 치우쳐진 데이터가 다수 존재하는데요. 아래에서 예를 들어보겠습니다.

위 예제를 보면 시험성적은 한쪽으로 치우쳐진 분포입니다. 이때 평균과 중위수를 구해보면 다소 차이가 나는 것을 볼 수 있는데요. 데이터의 분포가 대칭형태에 가까울수록 평균과 중위수가 비슷해지는 경향이 있습니다.

2. 분산(variance)와 표준편차(standard deviation)

위에서 살펴보았던 평균이나 중앙값은 데이터의 중심을 표현하는데 사용되는 값이라면, 분산과 표준편차는 데이터가 얼마나 넓게 퍼져있는지를 나타내는 값입니다. 이를 산포도라고 합니다.

2-1. 분산(variance)

분산은 평균에 대한 편차 제곱의 평균을 구한 값이다.

정의를 잠시 살펴보면, 분산은 편차 제곱의 평균이라고 적혀있습니다. 여기서 편차란 평균과의 차이인데요. 이 편차는 모두 합하면 0이 됩니다. 따라서 분산을 구하기 위해서는 편차 자체를 그냥 더하지 않고 제곱해서 더하는 과정을 거칩니다. 즉, 데이터가 평균에 가까울수록 편차는 작아지므로 분산은 작아지고, 평균과 멀리 떨어져있을수록 편차는 커지고 분산 또한 증가하게 되는 것입니다.

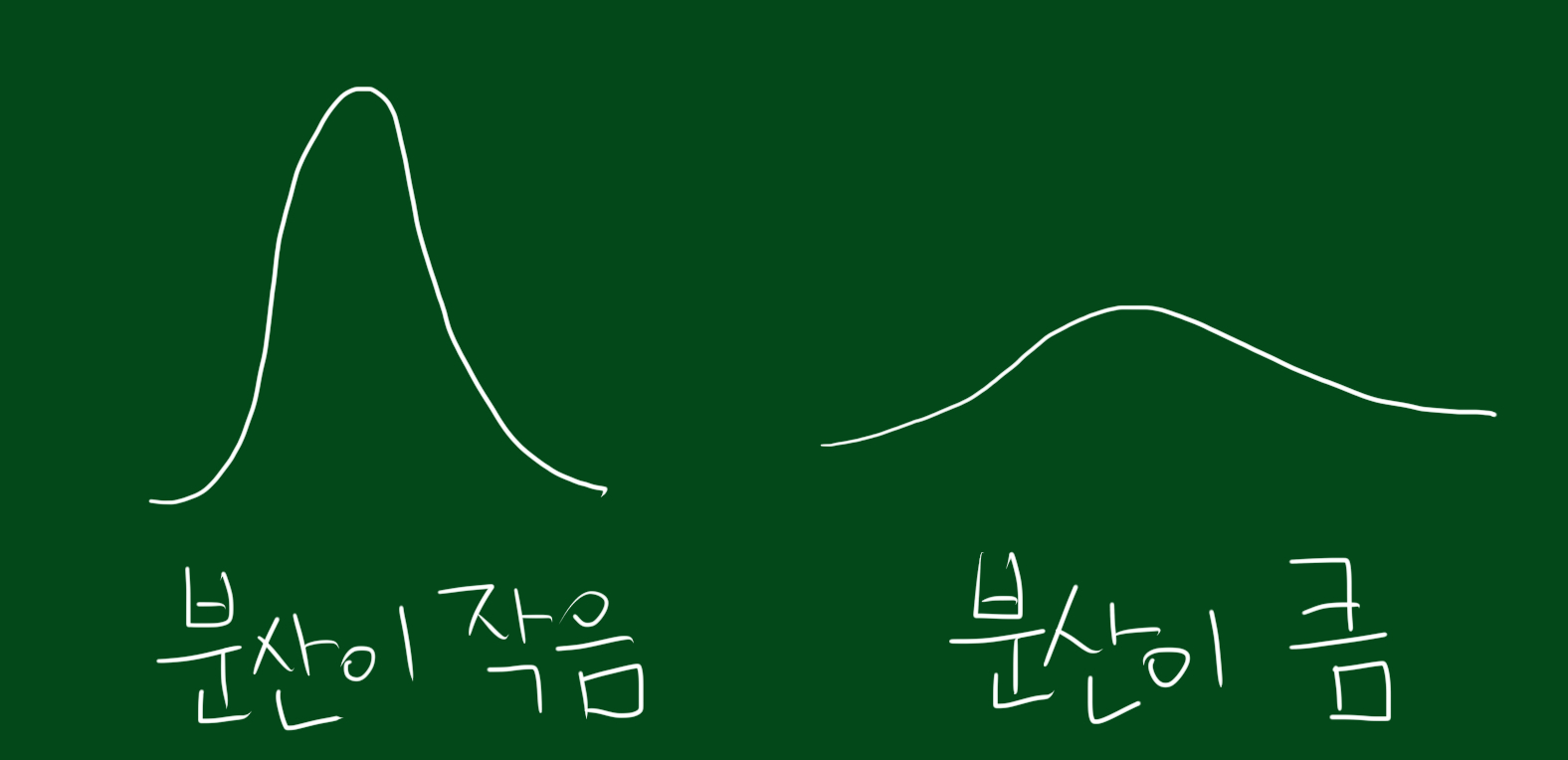
위 그림에서 알수 있듯, 데이터가 좁은 범위에 몰려있으면 분산이 작고, 데이터가 넓은 범위에 퍼져있다면 분산이 크다는 것을 알 수 있습니다.

2-2. 표준편차(standard deviation)

표준편차는 분산의 양의 제곱근으로 정의 된다.

위에서 분산은 데이터의 퍼짐정도를 나타낸다고 했습니다. 그럼 분산이 있는데 표준편차는 왜 필요할까요? 사실 분산에는 단점이 있습니다. 그것은 바로 편차를 ‘제곱’하면서 값이 크게 증가하는데요. 이렇게구한 분산은 값 자체의 의미를 파악하기 어려운 경향이 있습니다. 예를들어 시험점수 데이터라고 했을 때, 편차가 3이라면 우리는 3점차이 나는구나라고 직관적으로 이해할수있는데요. 이 값을 제곱하면 9가 되는데, 이 숫자가 무엇을 의미하는지 혼란스러울 수 있습니다. 따라서 표준편차는 분산에 루트를 씌우는 것은, 제곱하면서 증가했었던 값을 다시 원래 단위로 맞추는 과정이라고 이해하시면 되겠습니다. 만약 분산이 25라면 표준편차는 5가 되고, 우리는 5가 5점을 의미한다는 것을 알 수 있습니다.

3. 정리

위 내용을 종합하면 평균, 중앙값, 분산, 표준편차 등을 알면, 데이터전체를 확인하지 않더라도 전체 데이터가 어떤 형태를 띄는지 알 수 있습니다.