[기초통계] 정규분포 의미 및 개념 정리

정규분포 의미 및 개념 정리

참고링크

머신러닝	딥러닝	선형대수	기초통계	최적화
k-means	신경망이란	고유값,고유벡터	확률변수	컨벡스 셋
k-최근접이웃	성능함수	행렬식	확률분포	컨벡스 함수
선형회귀	신경망 학습	내적	모집단과 표본	라그랑주 듀얼
로지스틱회귀	교차연결	기저	평균과 분산	KKT 조건
릿지,라쏘회귀	합성곱 신경망	랭크, 차원	공분산, 상관계수	ROC 커브
의사결정나무	배치, 에포크 차이	선형변환	최대가능도추정	크로스 밸리데이션
서포트벡터머신	텐서플로기초(1)	직교행렬	베르누이,이항분포	실루엣 스코어
원클래스 SVM	텐서플로기초(2)	고유값분해	기하,음이항분포
LDA	seq2seq	특이값분해	초기하분포
GMM	opencv기초		포아송분포
부스팅	resnet		정규분포
사이킷런 실습	다각형내부판별		감마분포
	엣지판별		지수분포
			카이제곱분포
			베타분포
			균일분포

1. 정규분포의 정의

정규분포(normal distribution) 혹은 가우시안 분포(Gaussian distribution)은 연속확률분포의 하나이다. 정규분포는 수집된 자료의 분포를 근사하는데에 가주 사용되며, 이것은 중심극한정리에 의하여 독립적인 확률변수들의 평균은 정규분포에 가까워지는 성질이 있기 때문이다. 특히 평균이 0이고 표준편차가 1인 정규분포는 표준정규분포(standard normal distribution)이라고 한다.

정규분포는 여러가지 확률분포 중 가장 기초가 되는 분포입니다. 확률분포를 잘 모르시는 분리더라도 정규분포 혹은 종모양분포라는 말은 한번쯤은 들어보셨을 텐데요. 그만큼 중요한 분포입니다.

2. 정규분포의 확률밀도함수, 평균, 분산

정규분포의 확률밀도함수, 평균, 분산은 다음과 같습니다.

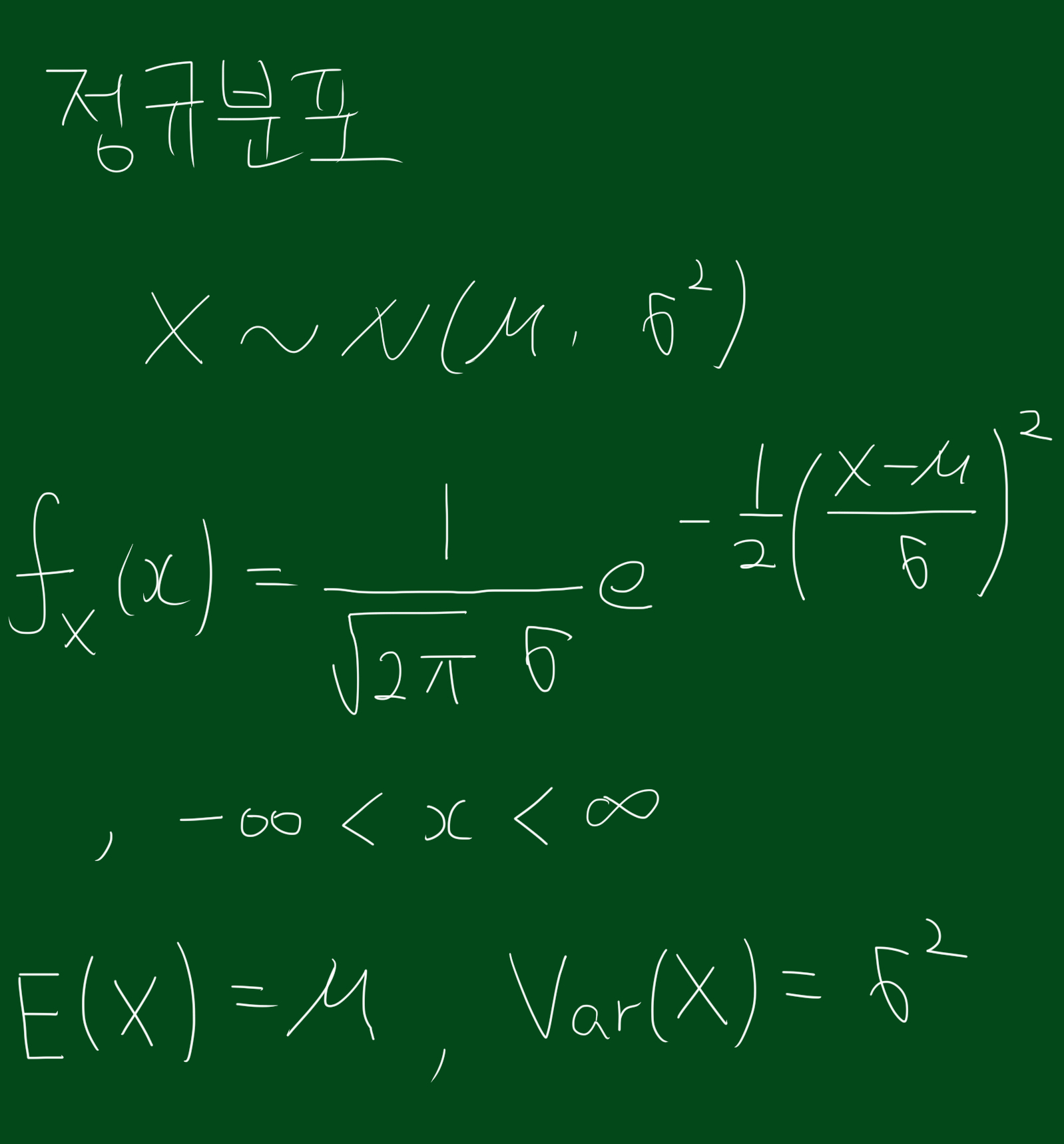
3. 중심극한정리

정규분포의 정의에서 중심극한정리(central limit theorem) 라는 말이 나오는데, 이름만 봐서는 중심으로 간다는 느낌이네요. 중심극한정리의 정의는 다음과 같습니다.

중심극한정리(central limit theorm, CLT)는 동일한 확률분포를 가진 독립확률변수 n개의 평균의 분포는 n이 적당히 크다면 정규분포에 가까워진다는 정리이다.

정의를 보면 이해하기 다소 어려우실수 있는데요. 우선 확률분포를 가진 독립확률변수라고 했으니 해당 확률변수는 평균과 분산을 가질 수 있겠죠. 이 때, 이 평균과 분산도 확률분포를 가지게 되는데요. 중심극한 정리는 n이 커진다면 그 확률분포가 정규분포에 가까워 진다는 뜻입니다.

4. 표준정규분포

표준정규분포(standard normal distribution)은 정규분포에서 평균이 0, 분산이 1인 경우를 의미합니다. 표준정규분포는 가설검정에서 많이 쓰이는데요. 흔히 z-검정, 표준정규분포표 라는 말을 들어보셨을 겁니다. 정규분포를 따르는 데이터셋에서 $ Z = \frac{X - \mu}{\sigma}$를 통해 $X$를 $Z$로 정규화시켜서 기존에 평균 $\mu$, ,분산 $\sigma^2$ 인 분포를 평균 0, 분산 1로 정규화시킵니다.

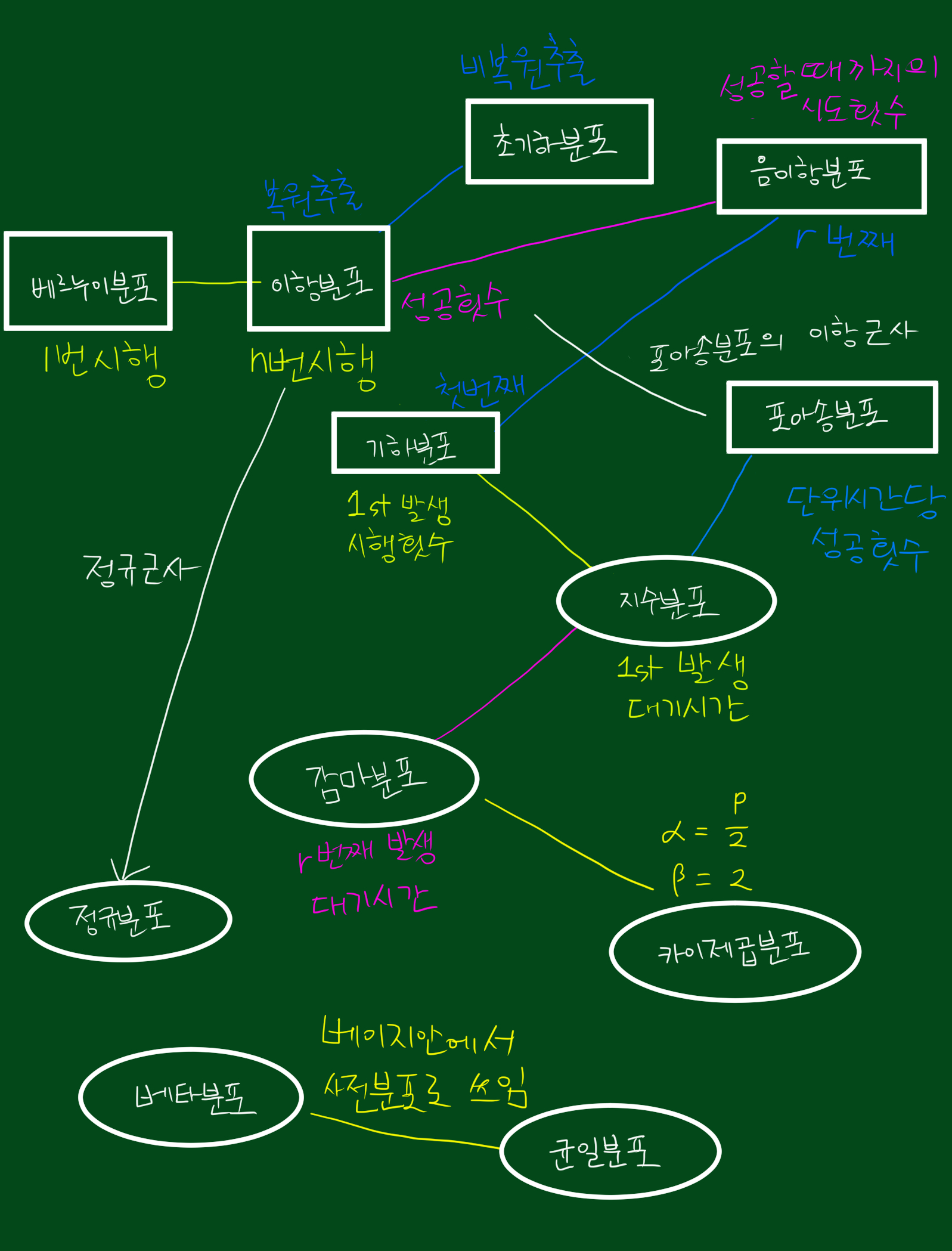
참고. 확률분포간 관계도