[머신러닝] 비지도학습 - One Class SVM
업데이트:
비지도학습 - One Class SVM(One Class Support Vector Machine)
참고링크
1. SVM 복습
우리는 지도학습 알고리즘 중 서포트 벡터 머신(support vector machine, 이하 SVM)이라는 알고리즘을 배웠습니다. 서포트 벡터 머신은 지도학습 알고리즘이므로 라벨링이 되어 있는 데이터를 대상으로 학습하는 알고리즘 입니다. 그리고 SVM 포스팅에서도 알 수 있듯, SVM의 핵심 개념은 서포트 벡터를 이용해 분류하는 것이었습니다.
2. One Class SVM의 목적
반면 이번 포스팅에서 알아볼 One Class SVM(one class support vector machine)은 비지도학습 알고리즘 중 하나입니다. 즉, one class svm은 서포트 벡터 개념을 이용해 라벨링되어 있지 않은 데이터를 클러스터링 하는 방법입니다.
이번 포스팅에서는 비지도학습에 사용되는 One Class SVM에 대해 알아보겠습니다.
위 그림을 보면 라벨링 되어 있지 않은 데이터들이 존재합니다. 우리의 목적은 위와 같은 데이터들을 다음 그림과 같이 이상치와 정상 데이터로 클러스터링 하는 것입니다.

그렇다면 위와 같이 클러스터링을 어떻게 할 수 있을까요?
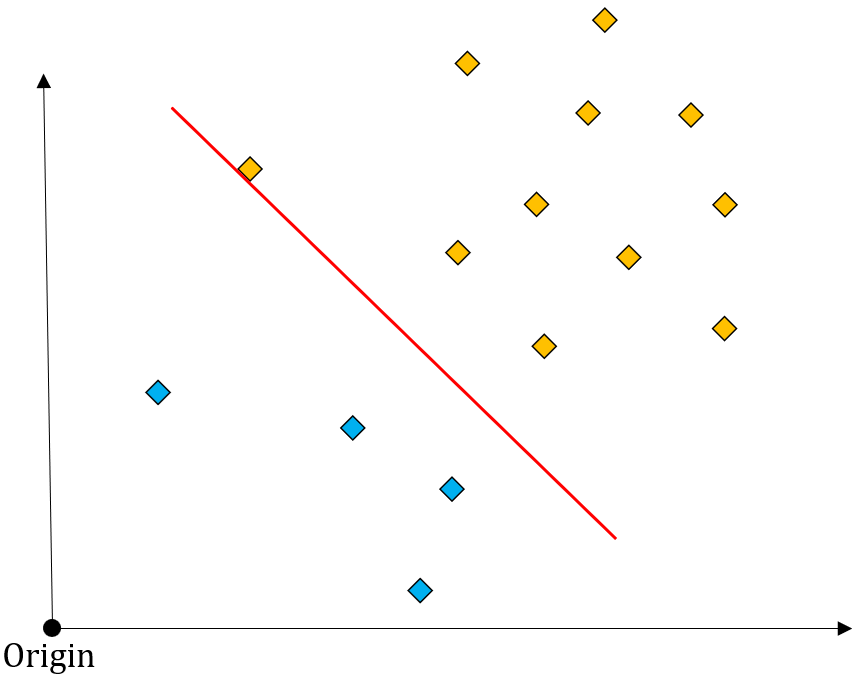
One Class SVM 또한 서포트 벡터를 활용하는 방법이므로 위 그림과 같이 정상 데이터와 이상치 데이터를 나누는 초평면(hyperplane)을 생성해 이를 기준으로 정상과 이상치를 구분할 수 있습니다.
3. One Class SVM의 개념
One Class SVM을 통한 클러스터링을 좀더 자세히 표현하면 다음과 같이 표현할 수 있습니다.
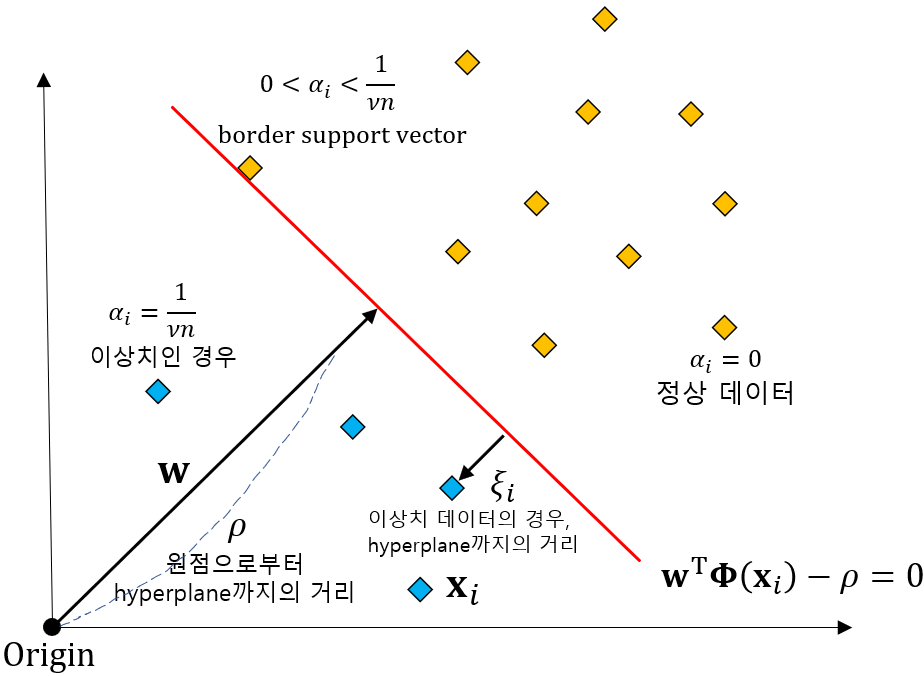
위 그림을 보면 일반적인 서포트 벡터 머신과 다르게 One Class SVM의 경우에는 원점에서 $w$벡터가 시작된다고 볼 수 있습니다. 그리고 원점으로부터 초평면까지의 거리를 $\rho$라고 하며, 우리의 목적은 초평면으로부터 데이터가 최대한 멀어지도록 초평면을 선정하는 것입니다. 그리고 초평면으로부터 이상치까지의 거리를 $\xi$라고 하겠습니다. 참고로 정상 데이터의 경우에는 $\xi$값이 0을 가집니다.
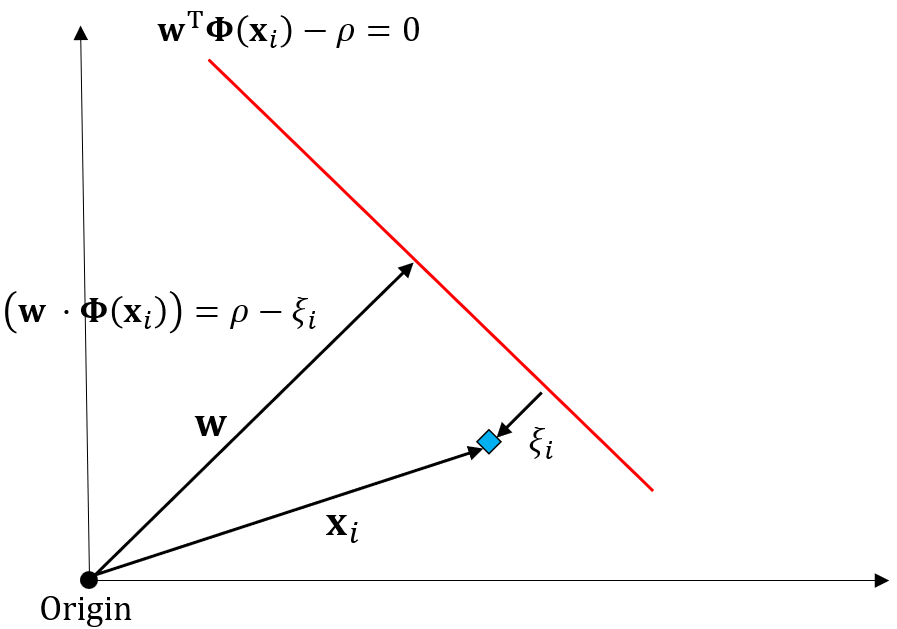
위 그림을 통해 이상치 데이터의 특징에 대해 좀 더 알아보겠습니다. 이상치 데이터의 경우 $w$ 벡터와 내적을 해서 $w^T x$값을 구해도 해당 값이 초평면을 넘어가지 못합니다. 이때 원점에서 초평면까지의 거리는 $\rho$이므로 $w^T x$값은 $\rho - \xi$가 됩니다.
4. One Class SVM 최적화 목적함수
기본적인 서포트 벡터 머신과 마찬가지로 one class svm 또한 다음과 같은 목적함수를 최적화 하는 방식입니다.

위 목적함수에서 $\phi (x)$는 새로운 피처 공간에서의 데이터를 의미합니다. 그리고 위 목적함수의 세번째 term인 $\rho$는 원점과 hyperplane과의 거리를 의미하며 이 거리를 최대화 해야합니다. 그러나 목적함수 자체가 최소화 시키는 $min$이 앞에 붙었으므로 거리 $\rho$에도 마이너스 부호를 붙여주어야 최대화 문제를 최소화 문제로 바꾸게 됩니다.
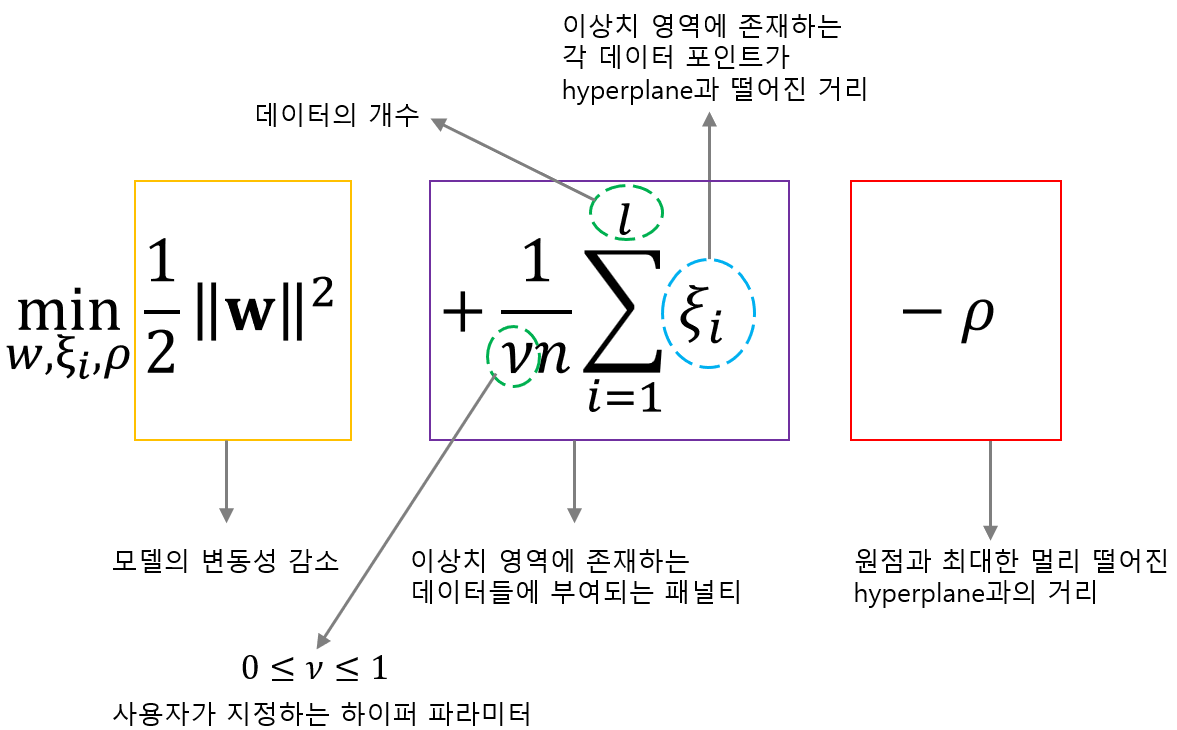
목적함수에 대해 좀 더 자세히 알아보겠습니다. 위 그림과 같이 첫번째 항은 모델의 변동성 감소를 위한 항입니다. 이는 Regularization 역할을 수행하는 것이며, 같은 값이라면 $x$의 변화에 따라 변동성이 크지 않도록 하기 위해서 $w$값을 최소화 시키는 방식을 활용합니다.
그리고 두번째 항을 보면 이는 이상치 영역에 존재하는 데이터들에게 부여되는 패널티 입니다. 정상 데이터의 경우 $\xi=0$인 반면, 이상치 영역에 존재하는 데이터들은 $\xi >0$이므로 이들의 합이라고 표현할 수 있습니다. 이때 $l$은 전체 데이터 개수를 나타내며 사실 익숙한 노테이션인 $n$으로 써도 되는데, One Class Svm을 설명하는 대부분의 분들이 $l$을 사용하므로 저도 $l$을 사용하겠습니다. $\nu$의 경우에는 사용자가 지정하는 하이퍼 파라미터인데, 0과 1사이의 값을 가지며 이 값에 따라 초평면의 형태가 변경됩니다. $\nu$값에 대해서는 이후에 더 자세히 설명하겠습니다.
마지막으로 세번째 항을 보면 이는 원점과 최대한 멀리 떨어진 초평면까지의 거리를 의미합니다.

목적함수의 제약식은 두가지가 존재하는데 위와 같이 첫번째 제약식을 먼저 보면, 위 제약식의 의미는 앞서 설명한 것 처럼 벡터 $w$와 데이터 포인트 $x_i$를 내적한 값은 $\rho - \xi_i$ 보다 크거나 같아야 한다는 의미입니다.
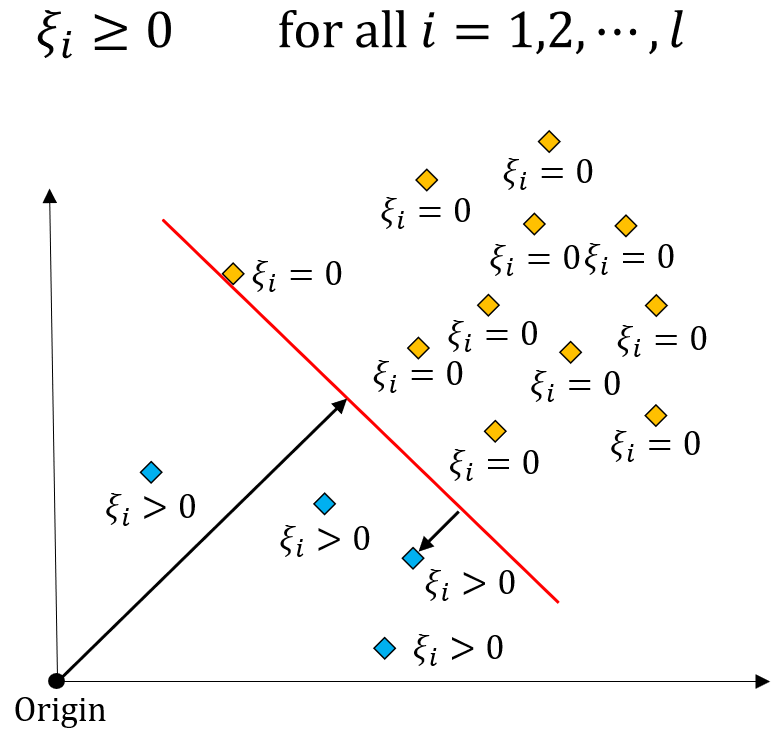
그리고 두번째 제약식의 의미는 위와 같습니다. 정상 데이터의 경우에는 $\xi_i$가 0이 되고, 이상치 데이터의 경우에는 $\xi_i > 0$이 됩니다.
5. One Class SVM 최적화 솔루션 구하기
앞서 배운 목적함수와 제약식을 한번에 표현하기 위해 대해 라그랑주 프리멀 함수를 구하면 다음과 같이 구할 수 있습니다.
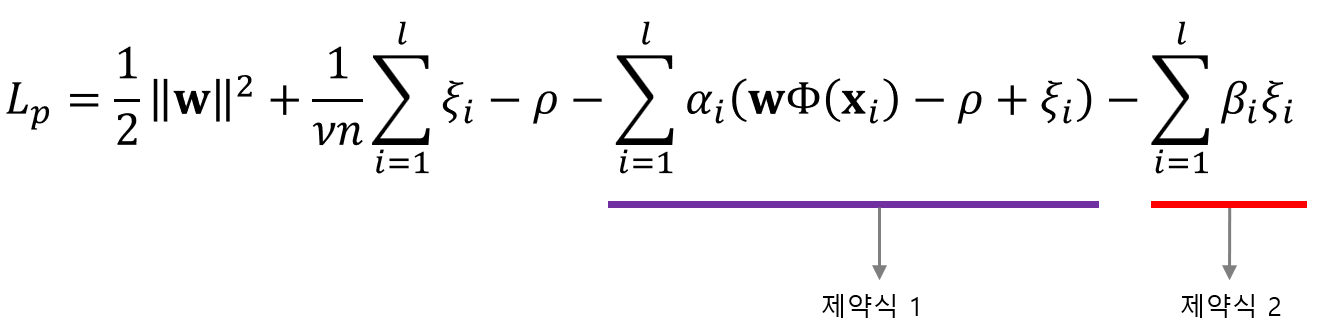
그리고 KKT 조건에 의해 각각의 파라미터로 편미분하면 다음과 같은 결과를 구할 수 있습니다.
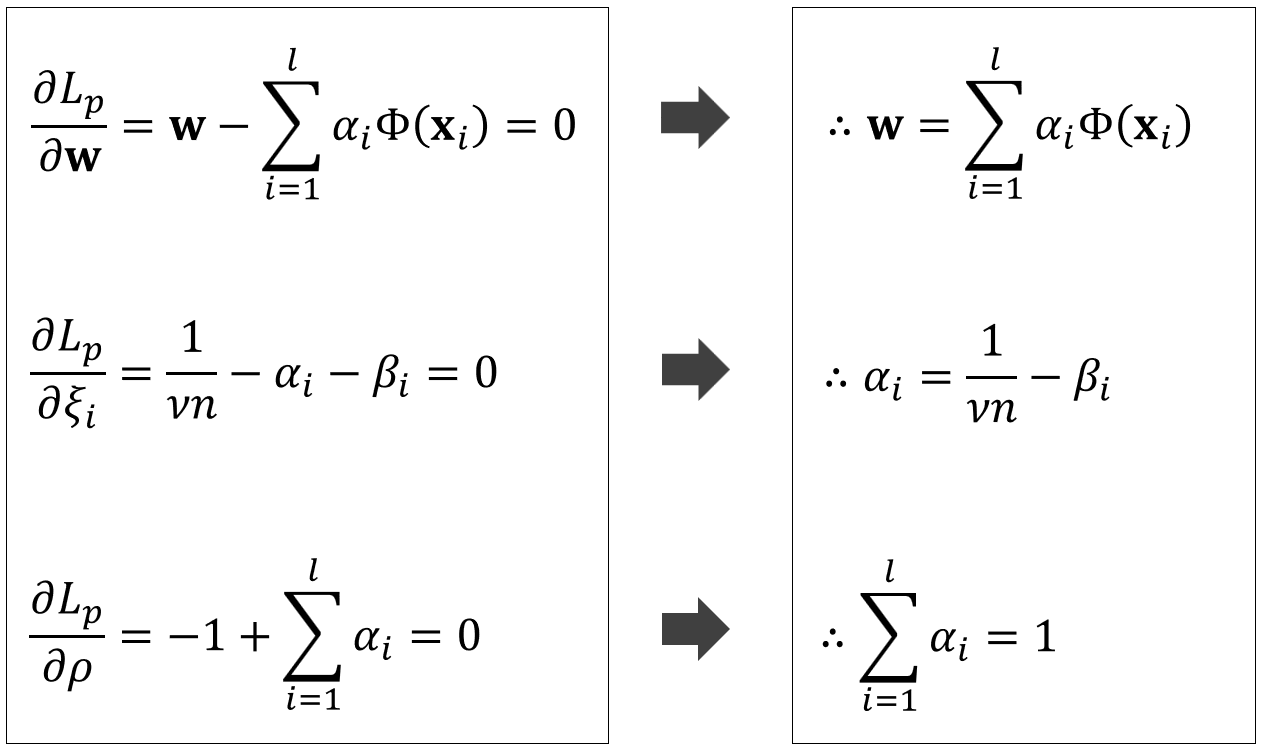
그리고 위에서 구한 $w$값을 다음 그림과 같이 다시 라그랑주 프리멀 함수에 넣어주겠습니다.
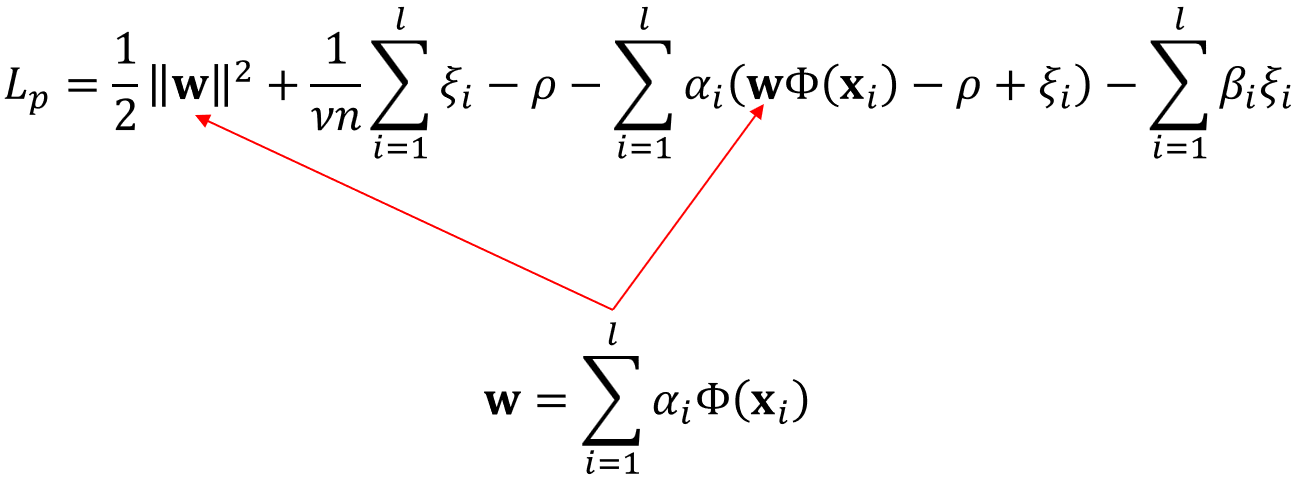
그러면 다음과 같이 라그랑주 듀얼 함수를 구할 수 있습니다.
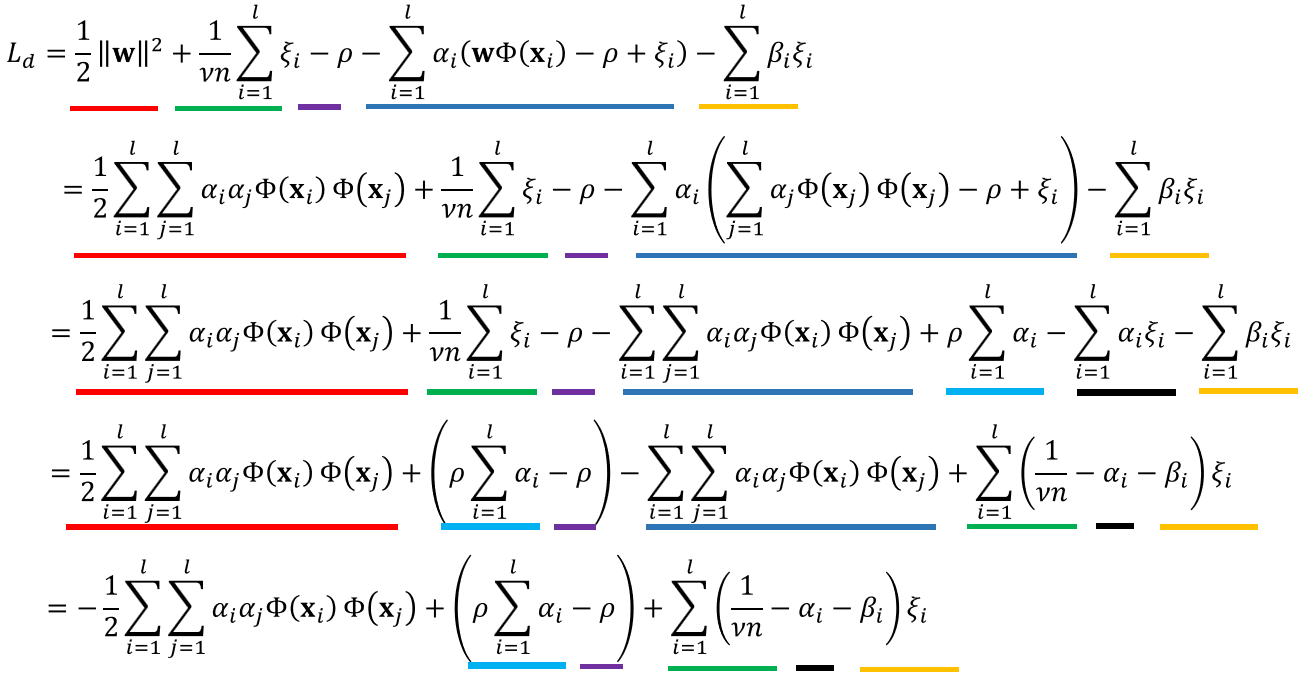
위에서 구한 라그랑주 듀얼 함수는 다음과 같이 깔끔하게 정리가 가능합니다.
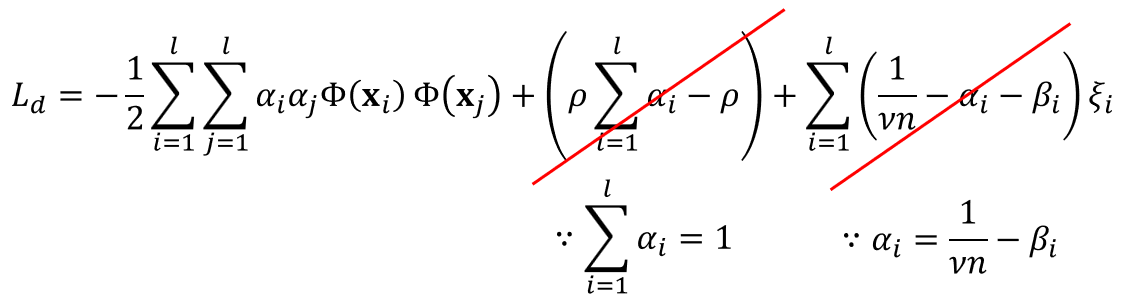
앞서 파라미터 편미분값을 이용하면 위와 같이 라그랑주 듀얼 함수의 두번째 항과 세번째 항이 깔끔하게 삭제 되는 것을 알 수 있습니다.
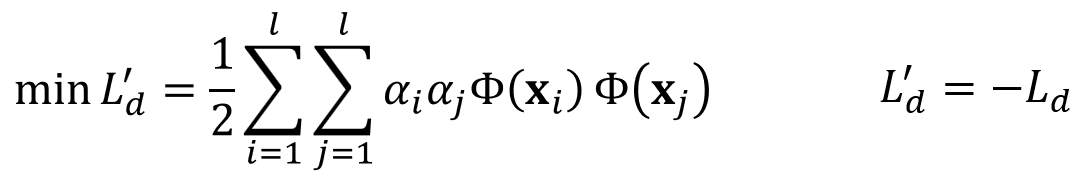
정리하면 위와 같이 최적화 문제를 정의할 수 있습니다.
5. One Class SVM 알파 값의 의미
그렇다면 앞서 언급한 최적화 문제에서 $\alpha$ 값이 의미하는 것은 무엇일까요?
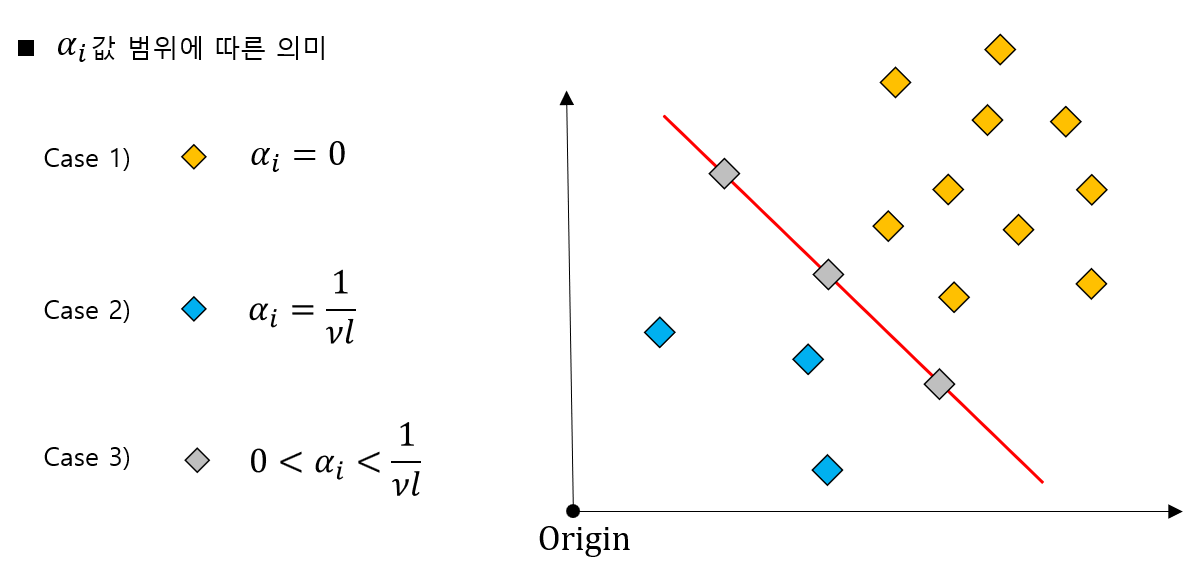
위 식과 같이 $\alpha$값의 범위에 따라 정상 데이터, 초평면 위에 걸쳐있는 데이터, 이상치 데이터로 구분할 수 있습니다. 각 조건들을 조금더 자세히 알아보겠습니다.

먼저 첫번째 조건을 정리하면 위와 같습니다. 위 정리는 $\alpha$값이 0일때 해당 데이터는 정상 데이터라는 것을 의미하는 그림입니다.

두번째 조건을 정리하면 위와 같습니다. 두번째 조건은 해당 조건을 만족하는 데이터는 이상치 데이터라는 의미입니다.
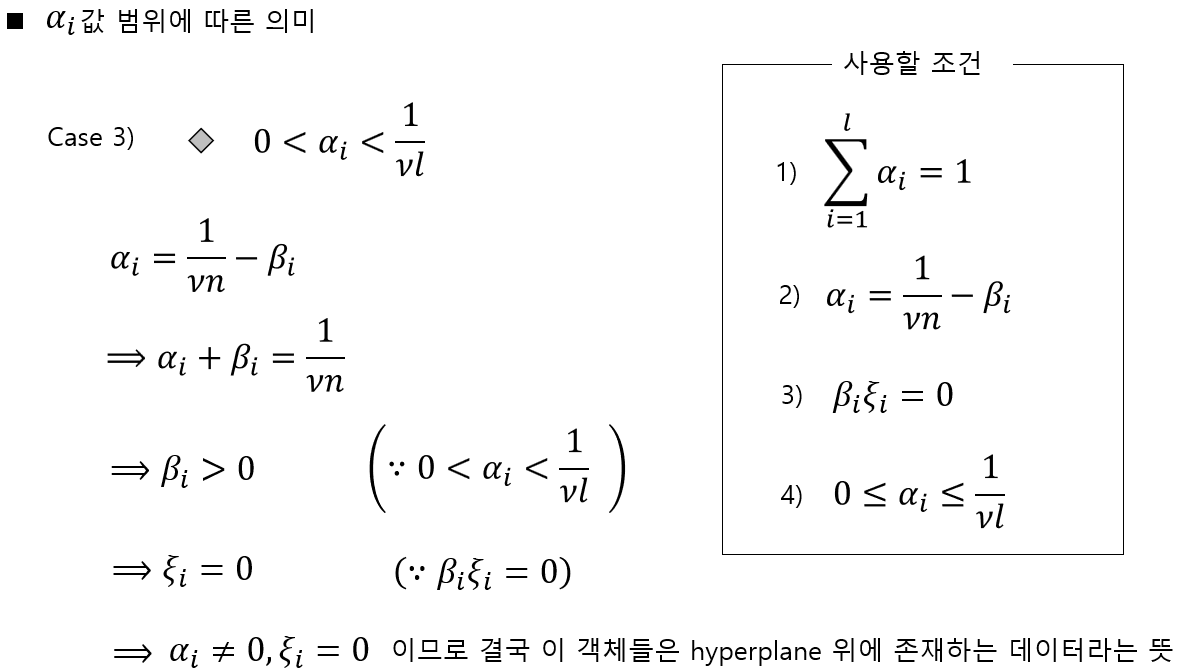
마지막 세번째 조건을 정리하면 위와 같습니다. 세번째 조건은 해당 조건을 만족하는 데이터는 초평면 위에 존재하는 데이터라는 의미입니다.
6. One Class SVM 누 값의 의미
이번에는 $\nu$값의 의미에 대해 알아보겠습니다. 이를 정리하면 다음과 같습니다.

결국 $\nu l$의 의미는 전체 데이터 중 이상치로 표현되는 최대 객체 수가 $vl$개라는 의미입니다. 또한 $\nu$의 의미는 서포트 벡터 개수의 하한임과 동시에 패널티가 부여되는 이상치 서포트 벡터 비율이 10%미만 이라는 뜻입니다. 결국 $\nu$값을 어떻게 정하느냐에 따라 결과물을 미리 예상할 수 있는 것입니다.
7. 사이킷 런에서의 One Class SVM 사용
파이썬에서는 사이킷런이라는 머신러닝 라이브러리를 제공합니다. 그리고 다음과 같이 one class svm을 쉽게 사용할 수 있습니다.
>>> from sklearn.svm import OneClassSVM
>>> X = [[0], [0.44], [0.45], [0.46], [1]]
>>> clf = OneClassSVM(gamma='auto').fit(X)
>>> clf.predict(X)
array([-1, 1, 1, 1, -1])
>>> clf.score_samples(X)
array([1.7798..., 2.0547..., 2.0556..., 2.0561..., 1.7332...])
8. 사이킷 런에서의 One Class SVM 성능 평가
One Class SVM은 비지도학습이므로 다음과 같이 실루엣 스코어를 사용해 쉽게 성능을 평가할 수 있습니다. 실루엣 스코어에 대한 자세한 설명은 링크를 참고해주세요.
>> from sklearn.metrics import silhouette_score
>> sil_score = silhouette_score(X, labels)
>> print(sil_score)
0.7598181300128782


